Навигация
Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов
3. Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов
Экспоненциальный (нормальный) закон распределения
Параметр закона распределения: ![]()
Таблица 4
| № | xi 103 км | fi шт | λ*xi | e-λ*xi | φ(xi) 10-6 | fi’ шт |
|
| 1 | 38,86 | 16 | 0,270 | 0,763 | 0,531 | 19,08 | 0,50 |
| 2 | 83,77 | 26 | 0,583 | 0,558 | 0,388 | 13,96 | 10,39 |
| 3 | 128,68 | 8 | 0,895 | 0,408 | 0,284 | 10,21 | 0,48 |
| 4 | 173,59 | 10 | 1,208 | 0,299 | 0,208 | 7,47 | 0,86 |
| 5 | 218,50 | 5 | 1,520 | 0,219 | 0,152 | 5,47 | 0,04 |
| 6 | 263,41 | 5 | 1,833 | 0,160 | 0,111 | 4,00 | 0,25 |
| 7 | 308,32 | 4 | 2,145 | 0,117 | 0,081 | 2,93 | 0,39 |
| 8 | 353,23 | 4 | 2,458 | 0,086 | 0,060 | 2,14 | 1,62 |
| 9 | 398,14 | 2 | 2,770 | 0,063 | 0,044 | 1,57 | 0,12 |
| ИТОГО: | 80 | 14,64 | |||||
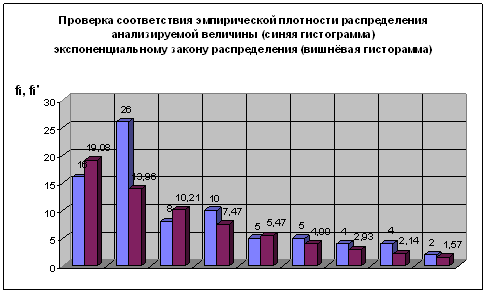
Рис. 4
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 7 и ![]() = 14,067.
= 14,067.
Так как χ2 > χ0,052, то гипотеза о принадлежности эмпирической выборки значений, экспоненциальному закону распределения отвергается
Распределение Вейбулла - Гнеденко
Величина выборочного коэффициента вариации:
![]()
По данным приложения таблица П1,2:
![]()
![]()

Таблица 5
| № | Xi 103 км | fi шт | xi/a | a* φ(xi) | φ(xi) 10-6 | fi’ шт |
|
| 1 | 38,86 | 16 | 0,246 | 0,6944 | 4,4017 | 15,81 | 0,00 |
| 2 | 83,77 | 26 | 0,531 | 0,7197 | 4,5618 | 16,39 | 5,63 |
| 3 | 128,68 | 8 | 0,816 | 0,6085 | 3,8567 | 13,86 | 2,48 |
| 4 | 173,59 | 10 | 1,100 | 0,4637 | 2,9393 | 10,56 | 0,03 |
| 5 | 218,50 | 5 | 1,385 | 0,3293 | 2,0870 | 7,50 | 0,83 |
| 6 | 263,41 | 5 | 1,670 | 0,2213 | 1,4029 | 5,04 | 0,00 |
| 7 | 308,32 | 4 | 1,954 | 0,1422 | 0,9014 | 3,24 | 0,18 |
| 8 | 353,23 | 4 | 2,239 | 0,0879 | 0,5570 | 2,00 | 2,00 |
| 9 | 398,14 | 2 | 2,524 | 0,0525 | 0,3325 | 1,19 | 0,54 |
| ИТОГО: | 80 | 75,60 | 11,69 | ||||
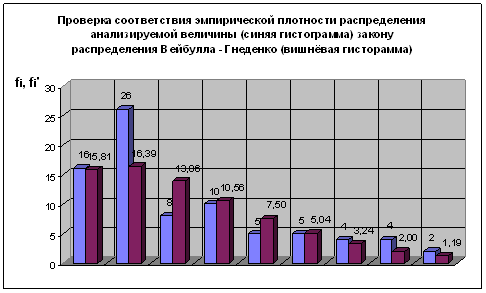
Рис. 5
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и ![]() = 12,592.
= 12,592.
Так как χ2 > χ0,052, то эмпирическая выборка значений пренадлежит закону распределения Вейбулла - Гнеденко
Нормальный (Гауссовский) закон распределения
Таблица 6
| № | Xi 103 км | fi | ti | φ(ti) 10-2 | φ(xi) | fi’ щт |
|
| 1 | 38,86 | 16 | -1,025 | 0,231 | 0,101 | 8,09 | 7,72 |
| 2 | 83,77 | 26 | -0,586 | 0,328 | 0,144 | 11,52 | 18,18 |
| 3 | 128,68 | 8 | -0,147 | 0,386 | 0,169 | 13,53 | 2,26 |
| 4 | 173,59 | 10 | 0,292 | 0,374 | 0,164 | 13,11 | 0,74 |
| 5 | 218,50 | 5 | 0,731 | 0,298 | 0,131 | 10,48 | 2,86 |
| 6 | 263,41 | 5 | 1,169 | 0,197 | 0,086 | 6,91 | 0,53 |
| 7 | 308,32 | 4 | 1,608 | 0,107 | 0,047 | 3,75 | 0,02 |
| 8 | 353,23 | 4 | 2,047 | 0,048 | 0,021 | 1,68 | 3,18 |
| 9 | 398,14 | 2 | 2,486 | 0,018 | 0,008 | 0,62 | 3,04 |
| ИТОГО: | 80 | 69,71 | 38,54 | ||||
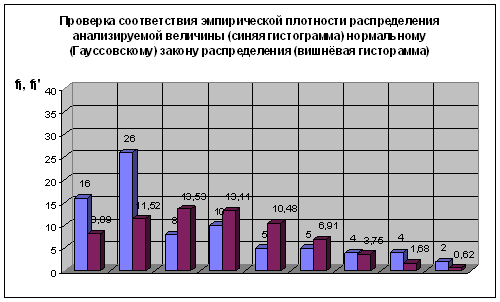
Рис. 6
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и ![]() = 12.592.
= 12.592.
Так как χ2 > χ0,052, то гипотеза о принадлежности эмпирической выборки значений, нормальному (Гауссовскому) закону распределения отвергается
Логарифмически - нормальный закон распределения
Значения средне-выборочное и средне-квадратичное:
![]()
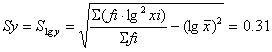
Таблица 7
| № | Xi 103 км | fi | ti | φ(ti) | φ(xi) | fi’ щт |
|
| 1 | 38,86 | 16 | -1,481 | 0,133 | 4,808 | 17,28 | 0,094 |
| 2 | 83,77 | 26 | -0,404 | 0,367 | 6,155 | 22,12 | 0,682 |
| 3 | 128,68 | 8 | 0,198 | 0,391 | 4,263 | 15,32 | 3,494 |
| 4 | 173,59 | 10 | 0,618 | 0,329 | 2,663 | 9,57 | 0,019 |
| 5 | 218,50 | 5 | 0,941 | 0,256 | 1,645 | 5,91 | 0,140 |
| 6 | 263,41 | 5 | 1,203 | 0,193 | 1,030 | 3,70 | 0,455 |
| 7 | 308,32 | 4 | 1,423 | 0,144 | 0,659 | 2,37 | 1,126 |
| 8 | 353,23 | 4 | 1,614 | 0,108 | 0,430 | 1,55 | 3,892 |
| 9 | 398,14 | 2 | 1,782 | 0,081 | 0,287 | 1,03 | 0,908 |
| ИТОГО: | 80 | 10,81 | |||||
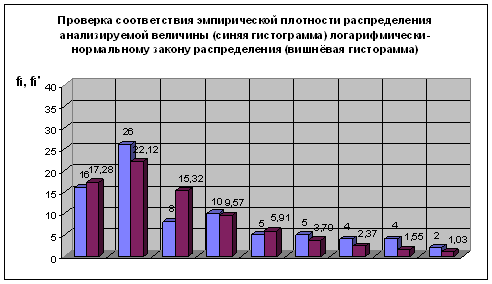
Рис. 7
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и ![]() = 12.592.
= 12.592.
Так как χ2 < χ0,052, то эмпирическая выборка значений принадлежит логарифмически-нормальному закону распределения
Похожие работы
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
... данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые исследуют в данном эксперименте. Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под ...
... вывод, что случайная величина распределена по равномерному закону, а случайная величина – по нормальному. Заключение В ходе курсовой работы были освоены методы обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов. Также в результате выполнения ...
... необходимо 24 образца. Неравномерное дублирование предполагает повторение экспериментов в каждой серии опытов неодинаковое число раз. На практике неравномерное дублирование экспериментов используется сравнительно редко из-за сложности построения регрессионных моделей по получаемым опытным данным. При решении прикладных задач материаловедения количество дублей в каждом опыте принимают не менее ...
0 комментариев