Навигация
Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ
УНИВЕРСИТЕТ имени ВЛАДИМИРА ДАЛЯ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКАк курсовой работе по дисциплине
“Организация эксперимента”
Тема: «Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента 23»
СТУДЕНТ: Черных Н.В.
ГРУППА: ММ – 961
РУКОВОДИТЕЛЬ: Шевченко А.В.
Луганск 2009 г.
Раздел 1. Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента 23
Принципы решения многофакторных оптимизационных задач. Метод крутого восхождения
Задачи материаловедения весьма разнообразны. В наиболее общем виде их можно разделить на две группы:
- экстремальные задачи, целью которых является поиск оптимальных в том или ином смысле составов материалов, режимов их термической обработки, условий литья, сварки, напыления, обработки давлением и т. п.;
- задачи описания, целью которых является изучение общих закономерностей явлений, происходящих в материалах при изменении их составов, в процессе их изготовления, во время последующих обработок. Задачи описания и экстремальные задачи часто решаются вместе.
Во всех случаях ситуация заметно упрощается, если для того или иного явления удается построить некоторую математическую модель.
Предположим, требуется изучить влияние химического состава, условий литья, обработки давлением и последующей термической обработки на свойства материалов выбранной системы. Целью этого исследования является попытка выявить общие закономерности изменения свойств материалов в зависимости от их химического состава и условий обработок, а также поиск материала, обладающего некоторым заданным комплексом свойств. Понятно, что цели исследования легко было бы достигнуть, если бы имелись математические модели, связывающие механические, технологические, эксплуатационные и любые другие свойства материалов изучаемой системы с их химическим составом, режимами литья, деформации, термической обработки, особенностями поверхностных свойств. Решение и задачи описания, и экстремальной задачи представляло бы тогда просто анализ имеющихся моделей.
Возникает вопрос, каким же образом получить такого рода модели? Существуют, по крайней мере, два способа.
Модели можно попытаться построить на основе знаний механизмов явлений, происходящих в материалах при изменении их состава и во время обработок, т. е. теоретическим путем. Построенные таким способом модели представляют исключительную ценность, поскольку их можно использовать не только для решения данной конкретной задачи, но и во многих других случаях.
К сожалению, механизмы большинства явлений или процессов, происходящих в различных материалах, к настоящему времени изучены явно недостаточно. Во всяком случае, строгих количественных теорий, как правило, не существует, а потому только из теоретических соображений построить модели для каждого конкретного случая почти никогда не удается. Тем не менее, рассматриваемая задача является стандартной в технологии металлов, материаловедении, порошковой металлургии и в технологии нанесения покрытий, а сами задачи такого рода, конечно же, решаются. Следовательно, решаются они при неполном знании (а иногда и вообще при незнании) механизмов явлений, протекающих в материалах. И способ решения вполне определенный – эмпирический, экспериментальный. Отсюда следует, что наиболее реалистичным путем построения математических моделей является эксперимент.
Итак, необходимо с помощью эксперимента, который будет проводиться при неполном знании или незнании механизмов явлений, научиться строить и анализировать математические модели, связывающие свойства материалов со всеми теми переменными, от которых эти свойства зависят.
Сразу же отметим, что поставленная проблема является задачей кибернетики. Действительно, если считать кибернетику наукой, изучающей системы любой природы, способные воспринимать, хранить и перерабатывать информацию для целей оптимального управления, то такой кибернетической системой в данном случае является исследуемый материал, и эту систему можно представить в виде так называемого “черного ящика”. Она будет иметь входы (независимые переменные, факторы) х1, х2, ..., xk (в нашем случае это состав, режимы литья, напыления, термической обработки, деформации) и выходы (зависимые переменные, отклики, параметры оптимизации, целевые функции) h1, h2, ..., hq (свойства материала). Существенным является то обстоятельство, что каждому набору уровней входов отвечают определенные значения выходов. Другими словами, сплав, порошковый материал или покрытие фиксированного состава, полученные и обработанные по определенной схеме и режимам, имеют некоторый комплекс свойств. Сплав другого состава, обработанный по другим режимам, имеет и другие свойства. Точно ответить на вопрос, почему при изменении состава и режимов обработок изменились свойства сплава, нельзя (механизм явления либо плохо, либо совсем не известен), но важен лишь сам факт изменения свойств. Если теперь предположить, что между выходами и входами системы существует определенная связь (а она, без сомнения, существует), задача сводится к постановке минимально возможного числа экспериментов (выбору некоторого числа наборов уровней входов), фиксации выходов, а затем к построению и анализу математических моделей, связывающих выходы с входами.
Таким образом, нужно получить некоторое представление о так называемых функциях отклика:
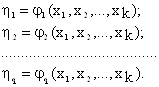
Вид функций j исследователю заранее неизвестен. Поэтому, получая в опытах выборочные оценки выходов y, он вынужден строить приближенные уравнения функций отклика:

Эти уравнения в многомерном пространстве факторов называются факторным пространством. Они имеют некоторый геометрический образ – поверхность отклика. Следовательно, задача сводится к получению представления о поверхности отклика. Если задача экстремальная, надо найти экстремум (минимум или максимум) этой поверхности или сделать вывод, что экстремума нет. Если решается задача описания, необходимо попытаться выявить причины именно такого характера поверхности.
Свойства материалов, как и вообще любых других систем, можно описывать различными математическими моделями. Наибольшее применение нашли модели в виде алгебраических полиномов. Обычно используют разложение неизвестной функции отклика в ряд Тейлора в окрестности любой точки из области ее определения в факторном пространстве:
![]()
где ![]() ;
;  ;
; 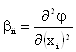 .
.
Этот степенной ряд в общем случае бесконечен, но на практике ограничиваются конечным числом его членов, аппроксимируя тем самым неизвестную функцию j (х1, х2,..., хk) полиномом некоторой степени. Подобная аппроксимация имеет смысл, если функция отвечает ряду требований. Важнейшим из них является требование непрерывности и достаточной «гладкости». Поскольку заранее неизвестно, насколько это требование выполняется, приходится делать допущения о том, что это так.
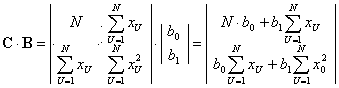
Модель строят по результатам экспериментов, т. е. определяют выборочные оценки коэффициентов b0, bi, bij, bii:
![]()
где у – выборочная оценка функции отклика h.
Эксперимент можно проводить по-разному. В случае, когда исследователь наблюдает за каким-то неуправляемым процессом, не вмешиваясь в него, или выбирает экспериментальные точки интуитивно, эксперимент считают пассивным. В частности, такая ситуация возникает почти всегда, когда пользуются традиционными методами экспериментирования, изучая вначале влияние на свойства материала одной переменной при остальных постоянных, затем другой и т. д. Поскольку при этом немыслимо перебрать все возможные варианты, выполняют лишь часть опытов, причем обоснование выбранных вариантов почти никогда не бывает достаточно строгим. В этих случаях статистические методы применяют обычно после окончания экспериментов, когда данные уже получены. Здесь используют такие приемы, как подбор функций распределения, определение средних величин и мер рассеяния, анализ корреляций, регрессий и т. п.
Опыт показал, что указанный подход, особенно в задачах оптимизации, является неэффективным. Не останавливаясь на всех причинах этого обстоятельства, отметим лишь, что по результатам пассивного эксперимента можно, например, судить о наличии или отсутствии статистической связи между переменными, построить подходящие уравнения связи. Но этими уравнениями можно пользоваться только для интерполяции. Например, можно оценить в виде аналитического выражения, как изменяется прочность того или иного материала в зависимости от его состава и условий изготовления, но интерпретировать полученную модель, придавать какое-либо значение ее коэффициентам, использовать для целей оптимизации, как правило, нельзя. В настоящее время пассивный эксперимент достаточно широко используют в технологии металлов и материаловедении. Тем не менее, будущее, вероятно, не за ним, хотя в некоторых случаях и из пассивных наблюдений удается извлечь весьма ценную информацию.
Совсем иная картина наблюдается, когда исследователь начинает применять статистические методы на всех этапах исследования и, прежде всего, перед постановкой опытов, разрабатывая схему эксперимента, а также в процессе экспериментирования, при обработке результатов и после эксперимента, принимая решение о дальнейших действиях. Такой эксперимент называют активным, и он предполагает планирование эксперимента.
Под планированием эксперимента обычно понимают процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
Основные преимущества активного эксперимента связаны с тем, что он позволяет:
- минимизировать общее число опытов;
- выбирать четкие, логически обоснованные процедуры, последовательно выполняемые экспериментатором при проведении исследования;
- использовать математический аппарат, формализующий многие действия экспериментатора;
- одновременно варьировать всеми переменными и оптимально использовать факторное пространство;
- организовать эксперимент таким образом, чтобы выполнялись многие исходные предпосылки регрессионного анализа;
- получать математические модели, имеющие более широкую область практического применения, нежели модели, построенные по результатам пассивного эксперимента;
- рандомизировать условия опытов, т. е. многочисленные несущественные факторы превратить в случайные величины;
- оценивать элемент неопределенности, связанный с экспериментом, что дает возможность сопоставлять результаты, получаемые разными исследователями.
Для того чтобы лучше себе представить, как реализуются идеи активного эксперимента, рассмотрим схему одного из наиболее широко используемых в настоящее время методов планирования эксперимента – метода крутого восхождения, предназначенного для решения экстремальных задач.
В этом методе, как и во многих других методах планирования эксперимента, задача решается поэтапно. На первом этапе, варьируя в каждом опыте сразу все факторы, исследователь ищет лишь направление движения к области экстремума. Для этого поверхность отклика изучают только на небольшом участке и строят для этого участка линейную модель:
![]() .
.
Анализ полученного уравнения позволяет наметить направление движения из исходной точки, наиболее быстро приводящее к оптимизации выбранного параметра. В дальнейшем на каждом этапе в соответствии с результатами, полученными на предыдущих этапах, ставят небольшую серию опытов, результаты которых вместе с интуитивными решениями исследователя определяют следующий шаг. Эта процедура заканчивается в области экстремума. Здесь ставят несколько большую серию опытов, и поверхность отклика описывают нелинейными функциями.
Анализ нелинейного уравнения позволяет точно определить координаты экстремума или сделать вывод, что экстремума не существует, а также наметить последующий путь оптимизации.
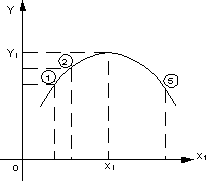
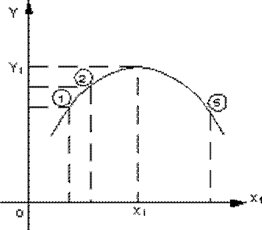
Сравним классический металловедческий подход и метод крутого восхождения на следующем примере. Предположим, что требуется найти состав наиболее прочного сплава на основе никеля, варьируя в нем содержание алюминия (х1) и тантала (х2). Предположим далее, что зависимость прочности (у) от состава для данных сплавов имеет вид, показанный на рис. 1, чего исследователь, приступая к решению задачи, естественно, не знает.
По интуитивным соображениям или на основании данных других исследований эксперимент начинают со сплава, отвечающего составу точки S1. При традиционном экспериментировании исследователь начинает изменять в этом сплаве содержание одной из добавок при постоянном количестве другой, затем содержание другой при постоянном количестве первой. При таком подходе, начиная с точки S1, вообще можно не найти оптимальный состав сплава (точка S6), поскольку движение по прямой от точки S1 в любую сторону не приводит к существенному упрочнению сплава (см. рис. 1).
Если далее экспериментатор сумеет перейти к другой исходной точке S2, то, последовательно изменяя содержание алюминия и тантала, он найдет наиболее прочный сплав, однако этот путь будет достаточно длинным (S2-S3-S4-S5-S6).
Таким образом, традиционное экспериментирование, предполагающее поочередное изменение переменных, ведет к нерациональному расходованию времени и средств, тем более, что большая часть информации, полученная после подобной работы, часто вообще не представляет практического интереса, поскольку относится к области, далекой от оптимальных условий.
Та же задача методом крутого восхождения решается следующим образом. Вблизи точки S1, начиная от которой при обычном экспериментировании успех вообще мог быть не достигнут, ставят небольшую серию из четырех опытов (точки 1, 2, 3, 4 на рис. 1). Цель этих опытов – еще не поиск состава наиболее прочного сплава. Определение прочности первых четырех сплавов позволяет исследователю приближенно описать неизвестную поверхность отклика на небольшом участке вблизи точки S1, т. е. рассчитать коэффициенты регрессии уравнения:
![]() .
.
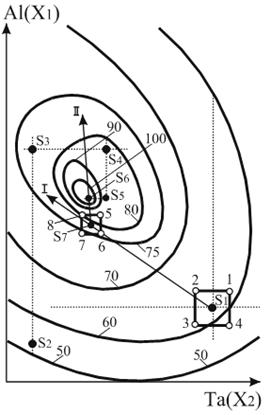
Рис. 1. Схема метода крутого восхождения: I – y = b0 + b1x1 + b2x2 ; II – y = b'0 + b'1x1 + b'2x2
Найденные по результатам опытов коэффициенты b1 и b2 определяют направление градиента для данной аппроксимирующей плоскости, т. е. направление изменения содержания алюминия и тантала в сплаве, приводящее к возможно более быстрому повышению прочности сплава. Сделав несколько опытов в этом направлении, т. е. осуществив крутое восхождение по поверхности отклика в направлении градиента линейного приближения (отсюда название метода), исследователь выбирает новую исходную точку S7, возле которой вновь проводит аналогичную серию из четырех опытов, рассчитывает коэффициенты нового линейного приближения теперь уже вблизи точки S7:
y = b'0 + b'1x1 + b'2x2
и осуществляет движение по градиенту этого уравнения. Движение по градиенту производят до попадания в область оптимума, после чего строят и анализируют нелинейную модель этой области. На рис. 1 градиент совпадает с прямой, перпендикулярной изолиниям, т. е. с самым крутым склоном, ведущим от данной точки к вершине. Для поверхности отклика, показанной на рис. 1, оказалось достаточно двух серий опытов, чтобы при крутом восхождении найти состав наиболее прочного сплава.
Даже рассмотренный пример показывает, что планирование эксперимента принципиально отличается от традиционного экспериментирования. При планировании используется многофакторная схема эксперимента, когда эффект влияния какого-либо фактора оценивается по результатам всех опытов. При традиционном экспериментировании (изменении одного фактора при постоянных остальных факторах) используется однофакторная схема, при которой эффект влияния фактора оценивается лишь по некоторой части опытов. Многофакторная схема существенно эффективней. Покажем это на простом примере.
Предположим, что необходимо определить массу трех образцов А, В и С. Рассмотрим два способа проведения эксперимента.
В первом случае схема взвешивания будет такой, как показано в табл. 1. Здесь первый опыт представляет собой холостое взвешивание, т. е. по сути дела, определение нулевого положения весов.
Следующие опыты – поочередное взвешивание каждого из образцов. Масса каждого образца оценивается по результатам только двух опытов: того опыта, в котором взвешивается образец, и холостого взвешивания. Например, масса образца А = у2 - у1; образца В = у3 - у1; образца С = у4 - у1.
Схема взвешивания во втором случае показана в табл. 2.
Здесь в первом опыте взвешивают все три образца вместе (холостое взвешивание не производится), а в следующих опытах – каждый образец в отдельности. В этом случае массу каждого образца оценивают по результатам всех опытов. Действительно, масса образца ![]() ; образца
; образца ![]() ; образца
; образца ![]() .
.
Таблица 1
Схема однофакторного эксперимента по взвешиванию образцов А, В и С
| Номер опыта | А | В | С | Результаты взвешивания |
| 1 | - | - | - | y1 |
| 2 | + | - | - | y2 |
| 3 | - | + | - | y3 |
| 4 | - | - | + | y4 |
Таблица 2
Схема многофакторного эксперимента по взвешиванию образцов А, В и С
| Номер опыта | А | В | С | Результаты взвешивания |
| 1 | + | + | + | y1 |
| 2 | + | - | - | y2 |
| 3 | - | + | - | y3 |
| 4 | - | - | + | y4 |
Какой же из способов взвешивания лучше? Будем считать лучшим способом тот, который дает более высокую точность. Если воспользоваться законом сложения дисперсий, для первого способа взвешивания получим:
![]()
где ![]() – дисперсия результатов взвешивания образцов; Sy – среднеквадратичная ошибка взвешивания.
– дисперсия результатов взвешивания образцов; Sy – среднеквадратичная ошибка взвешивания.
Для второго способа ![]()
Оказывается, второй способ обеспечивает точность вдвое выше по сравнению с первым, хотя общее число опытов в обоих случаях одинаково. Произошло это по вполне понятной причине. Первый способ взвешивания является традиционной схемой эксперимента – типичной однофакторной. Несмотря на то, что здесь всего было сделано четыре опыта, массу каждого образца определяли только по результатам взвешивания двух образцов. Второй же способ представляет собой схему многофакторного эксперимента. Здесь массу образца определяли по результатам всех опытов, а это и дает выигрыш в точности. Чтобы получить результаты с той же точностью при традиционном экспериментировании, придется повторить все опыты, т. е. проделать по сути дела вдвое большую работу. Легко показать, что с увеличением числа факторов эффективность многофакторного эксперимента растет.
Похожие работы
вание отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и ...
... qвос = 0,05 (в данном случае Gкр=0,3894), то гипотеза об однородности выборочных дисперсий отвечает результатам наблюдений. В данном случае воспроизводимость эксперимента выполняется. 2.4 Построение диаграммы рассеяния Вид диаграммы рассеяния приведен на рисунке 1. Рисунок 1 Рассчитанные значения вкладов и количество выделяющихся точек для соответствующих факторов приведены в ...
... планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; · планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; · планирование регрессионного эксперимента, позволяющего получать ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...


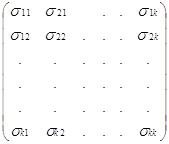

0 комментариев