Навигация
Количество групп равно 1+ 3,322lg30 = 1 + 3,322 х 1,48 = 4,4
1. Количество групп равно 1+ 3,322lg30 = 1 + 3,322 х 1,48 = 4,4
Принимаем число групп =5
Величина интервала равна (356139 – 2030,7) / 5 = 70821,7
Сгруппируем предприятия по размеру Валового регионального продукта (ВРП) в группы с интервалами 2030,7–72852,4; 72852,4–143674,1; 143674,1–214495,8; 214495,8–285317,5; 285317,5–356139.
2. Расчеты по каждой группе произведем в таблицах 3–5
Показатели по группам
Таблица 3. Группа №1
| № п/п | Валовой региональный продукт, млн. руб. | Уд. Вес, % | Общая численность населения, тыс. чел | Уд. Вес, % | Численность занятого населения, тыс. чел | Уд. Вес, % | Стоимость основных фондов, млн. руб. | Уд. Вес, % |
| 1 | 2030.7 | 0,5 | 460.1 | 3,0 | 59.4 | 0,9 | 5139 | 0,4 |
| 2 | 2127.1 | 0,6 | 314.3 | 2,1 | 117.4 | 1,9 | 21677 | 1,4 |
| 3 | 2443.5 | 0,7 | 195.6 | 1,3 | 71.2 | 1,2 | 20746 | 1,3 |
| 4 | 2568.1 | 0,7 | 204.8 | 1,3 | 84.3 | 1,4 | 15278 | 1,0 |
| 5 | 2616.3 | 0,7 | 310.7 | 2,0 | 99.2 | 1,6 | 14652 | 0,9 |
| 6 | 3212.1 | 0,8 | 75.3 | 0,5 | 32.7 | 0,5 | 18712 | 1,2 |
| 7 | 4317.5 | 1,1 | 430.7 | 2,8 | 139.4 | 2,3 | 32493 | 2,1 |
| 8 | 5110.2 | 1,3 | 446 | 2,9 | 156.8 | 2,5 | 47056 | 3,0 |
| 9 | 7572.3 | 2,0 | 677 | 4,4 | 227.2 | 3,7 | 43296 | 2,8 |
| 10 | 10467.7 | 2,7 | 755.2 | 4,9 | 333.4 | 5,4 | 95617 | 6,2 |
| 11 | 10529.8 | 2,8 | 783.9 | 5,1 | 303.7 | 4,9 | 48059 | 3,1 |
| 12 | 13043.6 | 3,4 | 2160.3 | 14,1 | 737.8 | 12,0 | 134133 | 8,6 |
| 13 | 14075.5 | 3,7 | 919.7 | 6,0 | 404.9 | 6,6 | 70373 | 4,5 |
| 14 | 14317.1 | 3,8 | 578.3 | 3,8 | 241 | 3,9 | 61889 | 4,0 |
| 15 | 15462.2 | 4,1 | 29.1 | 0,2 | 16.6 | 0,3 | 5497 | 0,4 |
| 16 | 18085 | 4,8 | 1026.3 | 6,7 | 395.5 | 6,4 | 91700 | 5,9 |
| 17 | 18372.1 | 4,8 | 1353.4 | 8,8 | 610.4 | 9,9 | 113170 | 7,3 |
| 18 | 20382.3 | 5,3 | 760.6 | 5,0 | 343.1 | 5,6 | 90800 | 5,8 |
| 19 | 22160.9 | 5,8 | 79.3 | 0,5 | 26.3 | 0,4 | 3742 | 0,2 |
| 20 | 37501.6 | 9,8 | 1623.8 | 10,6 | 767.8 | 12,5 | 180173 | 11,6 |
| 21 | 38994.1 | 10,2 | 45 | 0,3 | 21.4 | 0,3 | 17633 | 1,1 |
| 22 | 50914.3 | 13,4 | 1126.1 | 7,3 | 499.2 | 8,1 | 201201 | 13,0 |
| 23 | 64688 | 17,0 | 986 | 6,4 | 471.7 | 7,7 | 220865 | 14,2 |
| Итого | 380992 | 100,0 | 15341,5 | 100,0 | 6160,4 | 100,0 | 1553901 | 100,0 |
Таблица 4. Группа №2
| № п/п | Валовой региональный продукт, млн. руб. | Уд. Вес, % | Общая численность населения, тыс. чел | Уд. Вес, % | Численность занятого населения, тыс. чел | Уд. Вес, % | Стоимость основных фондов, млн. руб. | Уд. Вес, % |
| 1 | 85889,1 | 12,7 | 143 | 1,8 | 62,5 | 1,7 | 6335 | 0,7 |
| 2 | 94893,9 | 14,0 | 149,1 | 1,8 | 58,7 | 1,6 | 6370 | 0,7 |
| 3 | 114145,1 | 16,8 | 4101,7 | 49,8 | 1746,2 | 48,6 | 407013 | 45,0 |
| 4 | 123671,8 | 18,3 | 3776,8 | 45,9 | 1694 | 47,2 | 477390 | 52,8 |
| 5 | 129456,9 | 19,1 | 18,5 | 0,2 | 9,9 | 0,3 | 1842 | 0,2 |
| 6 | 129456,9 | 19,1 | 43,7 | 0,5 | 22,2 | 0,6 | 5400 | 0,6 |
| Итого | 677513,7 | 100,0 | 8232,8 | 100,0 | 3593,5 | 100,0 | 904350 | 100,0 |
Таблица 5. Группа №5
| № п/п | Валовой региональный продукт, млн. руб. | Уд. Вес, % | Общая численность населения, тыс. чел | Уд. Вес, % | Численность занятого населения, тыс. чел | Уд. Вес, % | Стоимость основных фондов, млн. руб. | Уд. Вес, % |
| 1 | 356139 | 100,0 | 1401,9 | 100,0 | 792 | 100,0 | 641474 | 100,0 |
| Итого | 356139 | 100,0 | 1401,9 | 100,0 | 792 | 100,0 | 641474 | 100,0 |
В основном, все регионы находятся в 1-й группе, но наибольшее количество ВРП производится в регионах, относящихся ко 2-й группе. Тем не менее, Хантымансийский а.о., при стоимости 1/5 основных фондов и удельном весе численности населения 5,6%, произвел валового регионального продукта в размере 25,2% от выборки.
Сводные данные приведем в таблице 6.
Таблица 6. Сводная группировка
| № группы | Валовой региональный продукт, млн. руб. | Уд. Вес, % | Общая численность населения, тыс. чел | Уд. Вес, % | Численность занятого населения, тыс. чел | Уд. Вес, % | Стоимость основных фондов, млн. руб. | Уд. Вес, % |
| 1 | 380992 | 26,9 | 15341,5 | 61,4 | 6160,4 | 58,4 | 1553901 | 50,1 |
| 2 | 677513,7 | 47,9 | 8232,8 | 33,0 | 3593,5 | 34,1 | 904350 | 29,2 |
| 3 | - | - | - | - | - | - | - | - |
| 4 | - | - | - | - | - | - | - | - |
| 5 | 356139 | 25,2 | 1401,9 | 5,6 | 792 | 7,5 | 641474 | 20,7 |
| Итого | 1414644,7 | 100,0 | 24976,2 | 100,0 | 10545,9 | 100,0 | 3099725 | 100,0 |
3. Зависимость валового регионального продукта от стоимости основных фондов – прямо пропорциональна, от численности занятого населения – обратно пропорциональна и зависит от природных богатств региона.
4. Полученная группировка нестандартна, так как отсутствуют 3,4 группы, но тем не менее, основное количество объектов исследования находится в 1-й группе, максимальные общие показатели находятся во 2-й группе, но при этом 5-я группа, несмотря на единственный объект, является лидером по всем показателям.
Задание №3
1. Определим нижнюю и верхнюю интервальные границы для каждой группы и составим рабочую таблицу, куда сведем первичный статистический материал:
Таблица 7. Рабочая таблица
| № группы | Валовой региональный продукт, млн. руб. | Количество регионов, Fj | Середина интервала, млн руб. Xj | Xj * Fj | Накопленная частота f |
| 1 | 2030,7–72852,4 | 23 | 37441,55 | 61155,65 | 23 |
| 2 | 72852,4–143674,1 | 6 | 108263,25 | 649579,5 | 29 |
| 3 | 143674,1–214495,8 | - | 179084,95 | - | 29 |
| 4 | 214495,8–285317,5 | - | 249906,65 | - | 29 |
| 5 | 285317,5–356139 | 1 | 320728,25 | 320728,25 | 30 |
| Итого | 30 | 1031463,4 |
Средняя арифметическая взвешенная:
Хср = 1031463,4 / 30 = 34382,1
Для определения показателей вариации вариационного ряда составим промежуточную таблицу на основе группировочной таблицы.
Таблица 8. Промежуточная таблица
| Середина интервала по группам, млн. руб. Х | Количество регионов, F | (X-Xcр) | │X-Xcр│ F | (X-Xcр)2 F |
| 37441,55 | 23 | 3059,45 | 70367,35 | 215285388,96 |
| 108263,25 | 6 | 73881,15 | 443286,9 | 32750545951,9 |
| 179084,95 | - | 144702,85 | - | - |
| 249906,65 | - | 215524,55 | - | - |
| 320728,25 | 1 | 286346,15 | 286346,15 | 81994117619,8 |
| Итого | 30 | 800000,4 | 114959948960,66 |
Размах вариации:
R =Xmax – Xmin=356139 – 2030,7 = 354108,3
Среднее линейное отклонение (взвешенное):
L =Σ (Х-Хср) F / n = 800000,4/30 = 266666,8 млн. руб.
Среднее квадратическое отклонение:
δ = √3831998298,68 = 61903,14
Дисперсия:
δ2 = 114959948960,66 / 30 = 3831998298,68
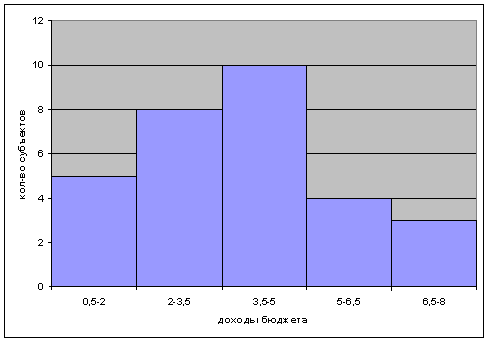
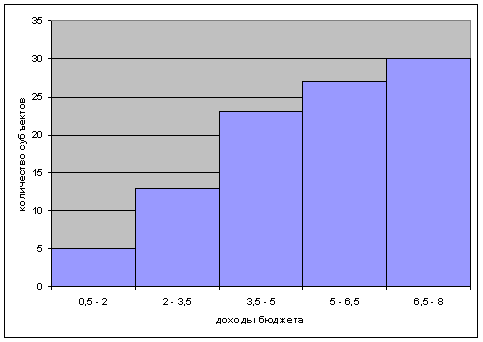
2. При построении гистограммы на оси абсцисс откладываются отрезки, соответствующие величине интервалов ряда. На отрезках строятся прямоугольники, площадь которых пропорциональна частотам интервала.
Вывод. По полученным графикам можно констатировать, что от группы к группе количество обследуемых объектов уменьшалось, при этом произошел разрыв между 2-й и 5-й группами, что подтверждается графиками гистограммы и полигона распределения. График куммуляты показывает, что от группы к группе нарастающим итогом происходило увеличение ВРП.
Средняя величина ВРП равна средней арифметической простой:
Хср = ∑Х / n = 1414644,7 / 30 = 47154,82
Коэффициент вариации V = 61903,14 / 34382,1 = 1,80
Модальным интервалом является интервал с наибольшей частотой. Моду в интервальном ряду находим по формуле
Мо = Хмо + I (Fmo – F-1) / ((Fmo – F-1) + (Fmo – F+1)), где
Хмо – начало модального интервала
Fmo – частота, соответствующая модальному интервалу
F-1 и F+1 – предмодальная и послемодальная частота
Мо = 2030,7 + 70821,7*(23–0) / ((23–0) +(23–6)) = 42753,18
Медианой называется вариант, который находится в середине вариационного ряда. В нашем случае это 15-й регион по порядку возрастания ВРП, т.е.
Ме=15462,2 млн. руб.
Квартили Q – значения признака в ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1, 25% единиц будут заключены межу Q1 и Q2, 25% – между Q2 и Q3, и остальные 25% превосходят Q3.
Q1= XQ1 + h ((n+1)/4 – S-1) / fQ1, где
XQ1 – нижняя граница интервала, в которой находится первая квартиль;
S-1 – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль;
fQ1 – частота интервала, в котором находится первая квартиль
Q1 =2030,7+70821,7 * (31/4–0)/ 23 = 25894,5
Q2 = 2030,7+70821,7*(31/2–0)/23 = 49758,4
Q3 = 72852,4+70821,7*(31*0,75–23)/23=144443,9
4. Проверим гипотезу о законе распределения с помощью критерия согласия Пирсона χ2.
Рассчитаем теоретические частоты попадания количества регионов в соответствующие группы. Х1 и Х2 – соответственно нижние и верхние границы интервалов. Т1 и Т2 – нормированные отклонения для нижней и верхней границ интервала. F1 и F2 – значения интегральной функции Лапласа для Т1 и Т2 – определяем по таблицам Лапласа. Оценка попадания случайной величины Р определяется как разница F(T1) – F(T2). Теоретическая частота f' = Р х 30. Составим таблицу 9.
Таблица 9. Расчет теоретических частот
| Границы интервала | Фактич. частота f | T1 = (Х1 – Хср) / σ | T2 = (Х2 – Хср) / σ | F(Т1) | F (Т2) | Р | Теоретич. частота f' |
| -∞ – 2030,7 | 0 | -∞ | -0,729 | -0,50 | -0,2673 | 0,2327 | 7 |
| -2030,7–72852,4 | 23 | -0,729 | 0,415 | -0,2673 | 0,1628 | 0,4301 | 13 |
| 72852,4–143674,1 | 6 | 0,415 | 1,559 | 0,1628 | 0,4406 | 0,2778 | 8 |
| 143674,1–214495,8 | 0 | 1,559 | 2,703 | 0,4406 | 0,4965 | 0,0559 | 2 |
| 214495,8–285317,5 | 0 | 2,703 | 3,847 | 0,4965 | 0,4999 | 0,0034 | 0 |
| 285317,5–356139 | 1 | 3,847 | 4,991 | 0,4999 | 0,5 | 0,0001 | 0 |
| 356139 – +∞ | 0 | 4,991 | +∞ | 0,5 | 0,5 | 0 | 0 |
| Итого | 30 | 1,00 | 30 |
Проверка показывает, что расчеты сделаны правильно, так как равен итог фактических и теоретических частот.
Рассчитаем значение χ2 = ∑ (f – f')2 / f', произведя расчеты в таблице
Оставляем 2 группы, объединив 1,2 в 1-ю группу, 3–7 во 2-ю группу. Результаты заносим в таблицу 10.
Таблица 10. Расчет фактического значения по критерию Пирсона
| Границы интервала | f – f' | (f – f')2 | (f – f')2 / f' |
| -∞ -72852,4 | 3 | 9 | 0,45 |
| 72852,4-+∞ | -3 | 9 | 0,9 |
| Итого | 1,35 |
Табличное значение критерия Пирсона при числе степеней свободы 1 и вероятности 0,99 составляет 1,64. Расчетное значение χ2 меньше табличного, поэтому гипотеза о близости эмпирического распределения к нормальному не отвергается.
Задание №4
1. По таблице случайных чисел определим порядковые номера и вид выборки. В выборочную совокупность войдут регионы по двум последним цифрам из 30 первых чисел подряд. Получаем:
12; 20; 22; 20; 24; 12.
Объем выборки – 6 единиц.
Получаем случайную повторную выборку. Величина ВРП:
13043,6; 13043,6; 37501,6; 37501,6; 50914,3; 85889,1.
Составим таблицу 11.
Таблица 11. Выборочная совокупность случайных величин
| Объем ВРП | 13043,6 | 37501,6 | 50914,3 | 85889,1 |
| Кол-во регионов | 2 | 2 | 1 | 1 |
Похожие работы
... М., 1995. 116. Клюкач В.А. Состояние и развитие аграрной экономической науки в России // Экономика сельскохозяйственных и перерабатывающих предприятий. – 2000. – №6. 117. Князева И.В. Антимонопольная политика в России:учебное пособие для студентов вузов обучающихся по специальности «Нац.экономика»/М.:Омега-Л, 2006. 526 с. 118. Ковалевская Л. Права надо защищать // Вечерний Ставрополь. ...
... пространстве России и ее северных территорий Расположенный в центральной части Западно-Сибирской низменности Ханты-Мансийский автономный округ в настоящее время представляет крупное административно-территориальное образование, являющееся субъектом Федерации и важнейшим по многим демографическим и экономическим параметрам регионом Российского Севера. Это самый крупный по численности ...
... пребывание в обследовании постоянного их круга и тем самым обеспечить большую адекватность социально-демографических характеристик домохозяйства аналогичным показателям по населению в целом. 5. Системы показателей Комплексное исследование качества жизни населения возможно только с помощью системы статистических показателей. В последние годы было предложено несколько систем, различающихся ...
... и косвенного воздействия на экономику являются: субсидирование предприятий, государственные инвестиции, бюджетное финансирование, субвенции и др. Расчетная часть Тема: Статистическое изучение объема, состава и динамики доходов и расходов государственного бюджета Имеются следующие выборочные данные (выборка 25%-ная механическая) о доходах и расходах бюджетов субъектов РФ за полугодие, млн. ...

0 комментариев