Анализ ряда распределения регионов по объёму промышленной продукции, млн. руб

2.2.2 Анализ ряда распределения регионов по объёму промышленной продукции, млн. руб.

Таблица 2.2 Распределение регионов по объёму промышленной продукции, млн. руб.

Группы регионов по объёму промышленной продукции, млн. руб. y	Число регионов, единиц fi	Середины интервалов yi	Накопленные частоты S	fi	Iyi -I	I-I 2 fi
11916 – 103110,17	24	57513,09	24	1380314,16	32359,23	25130874388,63
103110,17 – 194304,34	6	148707,3	30	892243,8	58834,98	20769329229,60
194304,34 – 285498,51	0	239901,4	30	0	150029,08	0
285498,51 – 376692,68	0	331095,6	30	0	241223,28	0
376692,68 – 467886,85	0	422289,8	30	0	332417,48	0
467886,85 - 559081	1	513483,9	31	513483,9	423611,58	179446770710,10
Итого:	31	-	-	2786041,86	-	225346974328,33

Среднее арифметическое значение признака:

=2786041,86/31=89872,32 (млн. руб.)

Вывод: среднее производство промышленной продукции в год составляет 89872,32 млн. руб.

Мода:

Mo=11916+9194,17*((24-0)/((24-0)+(24-6)))=17169,8 млн. руб.

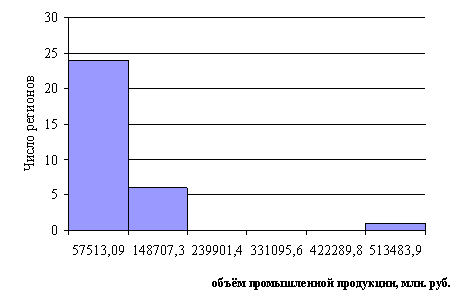
Рис. 2.7. Графическое представление моды с помощью гистограммы распределения объёма промышленной продукции, млн. руб.

Вывод: большинство регионов производит промышленной продукции - 17169,8 млн. руб.

Медиана:

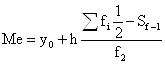
Me=11916+9194,17*((31/2-0)/24) =17853,9 млн. руб.

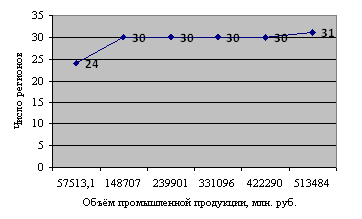
Рис. 2.8. Графическое представление медианы с помощью кумуляты распределения объёма промышленной продукции, млн. руб..

Вывод: половина регионов производит промышленной продукции более 17853,9 млн. руб., другая половина - менее 17853,9 млн. руб.

Среднеквадратическое отклонение:

 

=225346974328,33/31=7269257236,40 ()

==85259,93922 млн. руб.

Вывод: возможное отклонения объёма промышленной продукции от среднего объёма промышленной продукции составляет 85259,93922 млн. руб. (в год)

Коэффициент вариации:

=/*100%=85259,93922 /89872,32 *100%=95%

Вывод: совокупность не однородна, так как коэффициент вариации превышает 33%

  2.3 Проверка теоремы о разложении дисперсии

   

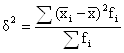
По 1 группе:

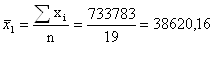
Таблица 2.3 Промежуточные показатели

16327	-22293,16	496984982,8
30406	-8214,16	67472424,51
32639	-5981,16	35774274,95
15127	-23493,16	551928566,8
38174	-446,16	199058,7456
59320	20699,84	428483376
60425	21804,84	475451047,4
29994	-8626,16	74410636,35
68499	29878,84	892745079,7
43512	4891,84	23930098,59
88196	49575,84	2457763912
18199	-20421,16	417023775,7
74326	35705,84	1274907010
51639	13018,84	169490194,9
23959	-14661,16	214949612,5
11916	-26704,16	713112161,3
22226	-16394,16	268768482,1
32579	-6041,16	36495614,15
16320	-22300,16	497297136
Итого		9097187445

По 2 группе:

Таблица 2.4 Промежуточные показатели

37634	-51285,83	2630236359
66707	-22212,83	493409816,6
143321	54401,17	2959487297
55840	-33079,83	1094275153
105129	16209,17	262737192,1
124888	35968,17	1293709253
Итого		8733855071

По 3 группе:

Таблица 2.5 Промежуточные результаты

125957	-173682,67	30165669858
213881	-85758,67	7354549480
559081	259441,33	67309803712
Итого		104830023050

По 4 группе:

Таблица 2.6 Промежуточные результаты

71134	-69309,5	4803806790
209753	69309,5	4803806790
Итого		9607613581

По 5 группе:

Таблица 2.7 Промежуточные результаты

174789	0	0
Итого	-	0

Средняя из внутригрупповых дисперсий:

Межгрупповая дисперсия:

 

Таблица 2.8 Промежуточные показатели

38620,16	-45957,16	2112060555	40129150550
88919,83	4342,51	18857393,1	113144358,6
299639,67	215062,35	46251814388	1,38755E+11
140443,5	55866,18	3121030068	6242060136
174789	90211,68	8138147208	8138147208
Итого	-	-	1,93*1011

 

Общая дисперсия по правилу сложения:

Общая дисперсия по формуле:

=

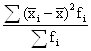
Среднее значение дисперсии:

Таблица 2.9 Промежуточные показатели

174789	90211,68	8138147208
16327	-68250,32	4658106180
30406	-54171,32	2934531911
32639	-51938,32	2697589084
15127	-69450,32	4823346948
38174	-46403,32	2153268107
59320	-25257,32	637932213,6
60425	-24152,32	583334561,4
29994	-54583,32	2979338822
68499	-16078,32	258512374
43512	-41065,32	1686360507
88196	3618,68	13094844,94
18199	-66378,32	4406081366
74326	-10251,32	105089561,7
51639	-32938,32	1084932924
23959	-60618,32	3674580720
11916	-72661,32	5279667424
125957	41379,68	1712277917
71134	-13443,32	180722852,6
37634	-46943,32	2203675293
66707	-17870,32	319348336,9
22226	-62351,32	3887687106
143321	58743,68	3450819940
213881	129303,68	16719441662
55840	-28737,32	825833560,8
32579	-51998,32	2703825283
16320	-68257,32	4659061734
209753	125175,68	15668950863
559081	474503,68	2,25154E+11
105129	20551,68	422371550,8
124888	40310,68	1624950922
Итого		3,25647E+11

=+-Теорема о разложении дисперсии.

10504729810 = 6237998239+4266731585 = 10504729824

Из проведённых расчётов видно, что общие дисперсии, рассчитанные различными способами, имеют небольшое отклонение, что и требовалось доказать.

2.4 Найти коэффициент детерминации

Вывод: фактор численности постоянного населения повлиял на производство промышленной продукции на 77%.
3. Задание №3   3.1.а Пределы, за которые не выйдет среднее значение признака

Т.к. по условию отбор – 35% бесповторный, и объем выборочной совокупности – 31 элементов, то объем генеральной совокупности будет равен 89 элементов(N). Т.к. p=0,954, то t=2.

Средняя ошибка выборки:

Предельная ошибка выборки:

 

Таким образом:

=2089,64

 

Вывод: с вероятностью 0,954 можно утверждать, что численность постоянного населения на конец года колеблется в пределах 1731,56 – 2447,72 тыс. чел.

  3.1.б Определение объема выборки для снижения предельной ошибки средней величины на 50%

Т.к. коэффициент доверия в данном случае является постоянным, то при снижении предельной ошибки выборки на 50% средняя ошибка выборки также уменьшится на 50%.

n = t²²N/(Δ²N + t²²), где:

n – объём выборочной совокупности;

t - коэффициент доверия;

 - среднее квадратическое отклонение;

N – объём генеральной совокупности;

Δ – предельная ошибка выборки;

t=2

Предельная ошибка равна 358,08 тыс. чел., если мы её снизим на 50% то она будет равна 179,04 тыс. чел.

Объём выборочной совокупности n = 31, после снижения предельной ошибки на 50% n – изменится.

n =  = = = 60,636

Вывод: Объем выборочной совокупности необходимо увеличить до 60,636 (61) элементов.

 

3.2.а Определение пределов, за которые не выйдет значение доли предприятий с индивидуальными значениями, превышающими моду

В данном случае отбор повторный, выберем p=0,683; тогда t=1; количество предприятий с индивидуальными значениями признака, превышающими моду, равно 27.

Mo=17169,8 кг

Их доля равна:

Предельная ошибка выборки равна:

 

Таким образом:

т.е.:

Вывод: значение доли предприятий с индивидуальными значениями, превышающими моду, находятся в интервале от 0,81% до 0,93%.

  3.2.б Определение объема выборки для снижения предельной ошибки доли на 20%

Предельная ошибка выборки:

Имеем:

тогда n=49,1

 

Вывод: для снижения предельной ошибки на 20% необходимо увеличить объем выборки до 49,1 (49) элементов.

4. Задание №4