Детерминированные модели управления запасами

2.  Детерминированные модели управления запасами

Рассмотрим метод расчета параметров оптимальных стратегий при детерминированном стационарном спросе на изолированном складе при следующих предложениях:

1)  Продолжительность планового периода неограниченна;

2)  Интенсивности спроса и поставок постоянны и равны µ и λ соответственно;

3)  Время и уровни запасов описываются непрерывными переменными;

4)  Накладные расходы на запуск производства постоянны и равны g;

5)  Затраты на содержание запасов и издержки, вызванные дефицитом, пропорциональны среднему уровню запасов и среднему уровню дефицита соответственно; h – стоимость хранения одного изделия в течении единицы времени; p – штрафные потери за нехватку одного изделия в течение единицы времени.

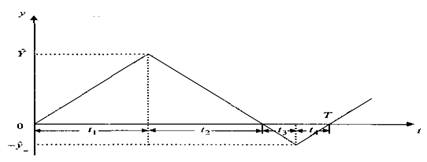
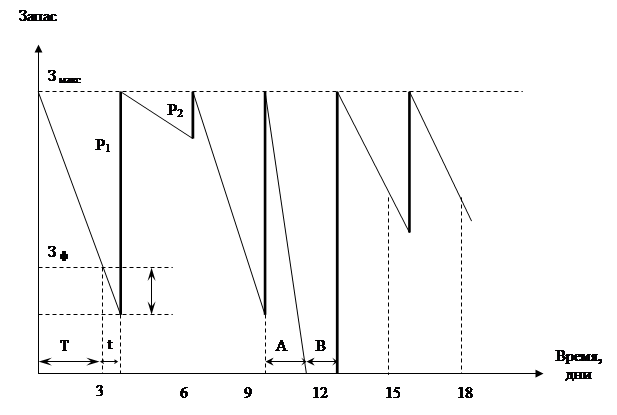
Динамика изменения уровня запаса при детерминированном спроса показана на рис. 1.

Полный цикл работы склада имеет положительность Т. Обозначим через предельный запас на складе. Считая расходы на хранение (и штрафы) пропорциональными среднему запасу (дефициту) и времени их существования, получаем следующее выражение для функции затрат за цикл:

 

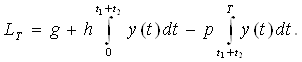
Очевидно, что

Максимальный дефицит _ выражается через  как

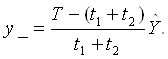
Подставим  и 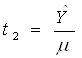, и получаем

.

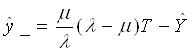Перепишем функцию затрат с учетом линейности изменения уровня запаса:

.

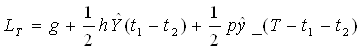В развернутом виде

,

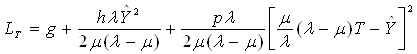оттуда затраты в единицу времени

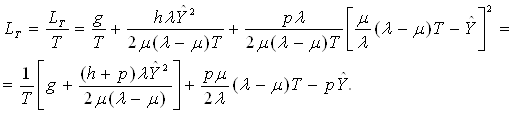
(2.1)

Найдем частные производные от L₁ по  и T и приравняем их к нулю:

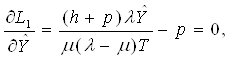(2.2)

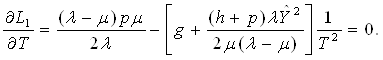(2.3)

Совместимое решение этих уравнений дает для оптимальных  и Т условия

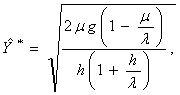
(2.4)

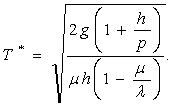(2.5)

При этом достигается минимум затрат в единице времени

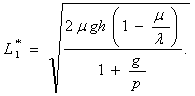 .(2.6)

Момент запуска производства определяется достижением наибольшего дефицита

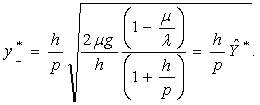(2.7)

Из полученных соотношений как частные случаи легко выводятся более известные формулы запасов.

Так, например, при высоком штрафе можно принять

При этом

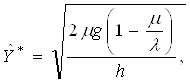(2.8)

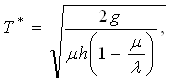(2.9)

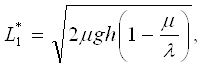(2.10)

а недостачи полностью исключаются (_=0).

Другой частный случай соответствует высокой интенсивности восполнения запаса  – условие, типичное для поставок с вышестоящего склада, когда весь объем затребованной партии отгружается разом. В этой модели

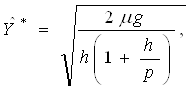(2.11)

(2.12)

(2.13)

Наиболее широкое применение нашли формулы, выведенные при обоих рассмотренных допущениях (так называемые формулы Уилсона, полученные еще в 20-х годах):

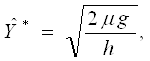(2.14)

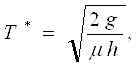(2.15)

(2.16)

o  Пример 1. Нахождение оптимальных размеров заказываемой партии, интервал между заказами и общих среднесуточных издержек.

На склад цемент доставляют на багаже. Накладные расходы на запуск производства цемента и доставку его на склад равны 1960 руб. Издержки хранения 1 т цемента в течение суток составляют 10 коп. Найти оптимальные : размер заказываемой партии цемента, интервал времени между заказами поставок, среднесуточные общие издержки, если поставки осуществляются без задержки – мгновенно, а дефицит не допускается.

Исходные данные задачи: µ = 50т/сут, g = 1960 руб.,/(т·сут), h/p = 0, _ = 0.

Для решения задачи используем формулы Уилсона (2.14) – (2.16). оптимальный размер заказываемой партии:

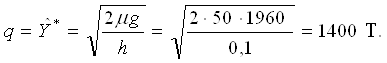
Интервал между заказами:

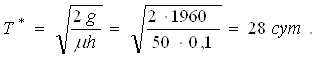
Общие среднесуточные издержки:

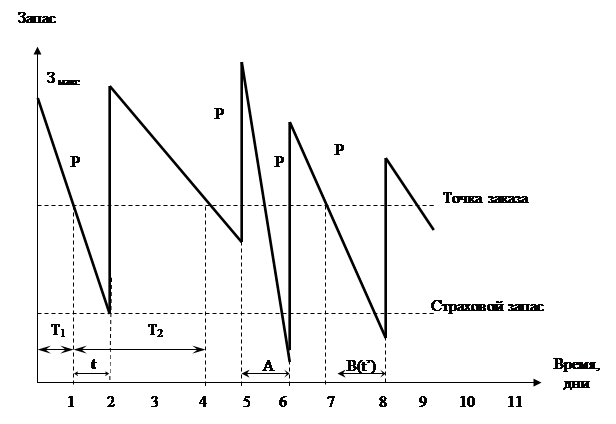
Помимо рассмотренных выше показателей представляют интерес еще два – объем заказываемой партии q и точка заказа  при задержке τ между заказом и началом поставки. Первый из них равен спросу µТ за период, так что для общего случая

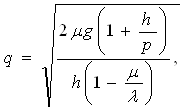(2.17)

а при µ/λ→0

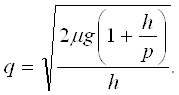(2.18)

В моделях с высоким штрафом  Точка заказа при задержке поставок определяется как –

Входящие в формулы данной курсовой экономические коэффициенты можно считать постоянными лишь в первом приближении – в некотором диапазоне объемов партий q. Так, цена заказа g и цена хранения h могут быть ступенчатыми возрастающими функциями q (при увеличении q, вероятно, потребуются дополнительные затраты на организацию производства, новые складские емкости). В подобных случаях необходимо задать некоторые априорное значение q₀ ( например, середину допустимого диапазона), рассчитать h(q₀) и g(q₀) и по приведенным выше формулам найти q₁.

Если h(q₀) = h(q₁) и g(q₀)= g(q₁), полученное значение q является окончательным. В противном случае вычисления повторяются при h(q₁) и g(q₁) и т.д. последовательные приближения, как правило, сходятся к искомому решению достаточно быстро.

Практический интерес вызывает задача определения продажной цены изделия S с учетом зависимости от нее интенсивности спроса µ. Будем считать, что спрос обеспечивается полностью, а себестоимость единицы продукции составляет u. Используя (2.10), можно для дохода в единицу времени записать выражение

(2.19)

Максимальный доход достигается при или при

(2.20)

Решать подобные уравнения удобно графически.