Навигация
Динамическая модель управления запасами
4. Динамическая модель управления запасами
Рассмотрим предприятие, которое изготовляет партиями некоторые изделия. Оно состоит из производственных цехов и склада для хранения готовой продукции. Предположим, что предприятие получило заказы на продукцию на n месяцев (этапов) вперед. Эти заказы необходимо полностью и своевременно выполнять (дефицит не допускается). Для разных этапов спрос не одинаков, кроме того, на экономические показатели производства влияют размеры изготовляемых партий продукции. Поэтому предприятию иногда бывает выгодно производить в течение месяца продукцию в объеме, превышающем спрос в пределах этого этапа, и хранить запасы «лишней» продукции, используя их для удовлетворения последующего спроса. Продолжительность изготовления партии изделий будем считать пренебрежимо малой (однако это требование может быть изменено в соответствии с особенностями технологического процесса). Цель предприятия – выработать такую программу производства, которая обеспечила бы минимальные затраты на изготовление и хранения продукции.
Введем обозначения:
xt – число изделий, изготовленных в t-м месяце (этапе);
yt – уровень запасов на конец t-го месяца;
dt – спрос на изделие в t-м месяце;
ft(xt, yt) – затраты на производство и хранение изделий в t-м месяце.
Соотношение материального базиса примет вид
![]() (4.1)
(4.1)
т.е уровень запасов на конец t-го этапа равен сумме уровня запасов на начало t-го и объема производства на t-м этапе за вычетом спроса на t-м этапе.
Данное балансовое соотношение можно записать и в другом виде:
![]() (4.2)
(4.2)
Наша задача состоит в том, чтобы составить такой план производства
X = (x1, …,xn), или, что тоже самое, найти такой план хранения запасов Y = (y1, …,yn), который обеспечил бы минимальные суммарные затраты предприятия
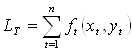 (4.3)
(4.3)
за весь плановый период.
Введем ограничения на переменные xt, yt. Будем считать объемы производства и уровни хранения на каждом этапе неотрицательными и целочисленными величинами. Кроме того, предположим, что уровни запасов к началу первого этапа y0 и к концу последнего yn заранее известны.
Решим сформулированную задачу методом динамического программирования. В качестве параметра состояния ζ примем уровень запасов на конец k-го этапа
![]() . (4.4)
. (4.4)
Функцию составления ![]() определим как минимальные затраты за первые k месяцев, т.е.
определим как минимальные затраты за первые k месяцев, т.е.
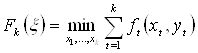 . (4.5)
. (4.5)
Здесь абсолютный минимум берется по всем значениям x1, …,xk, удовлетворяющим балансовым уравнениям:
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
При k = 1 соотношение (4.7) примет вид
![]() (4.8)
(4.8)
или
![]() . (4.9)
. (4.9)
Тогда с учетом (4.4) и (4.9) функция состояния
![]() , (4.10)
, (4.10)
причем если не видно никаких ограничений на объем складских помещений и производственную мощность предприятия, то ![]()
![]() ,
,
![]() . (4.11)
. (4.11)
Это связано с тем обстоятельством, что если иметь на конец 1-го этапа запас изделий в качестве ![]() , то, ничего не изготовляя в течение всего планового периода, а только удовлетворяя спрос, можно выйти на уровень запасов yn в конце n-го месяца. В то же время если уровень запасов на начало 1-го этапа равен y0, то, изготовив в 1-м месяце изделий в количестве
, то, ничего не изготовляя в течение всего планового периода, а только удовлетворяя спрос, можно выйти на уровень запасов yn в конце n-го месяца. В то же время если уровень запасов на начало 1-го этапа равен y0, то, изготовив в 1-м месяце изделий в количестве ![]() и не производя ничего на последних этапах, получим тот же запас yn в конце планового периода. Если же на 1-м этапе предприятие может вместить готовой продукции не более М1 изделий, а мощности предприятия не позволяют произвести более N1 изделий, то
и не производя ничего на последних этапах, получим тот же запас yn в конце планового периода. Если же на 1-м этапе предприятие может вместить готовой продукции не более М1 изделий, а мощности предприятия не позволяют произвести более N1 изделий, то ![]()
![]() ,
,
![]() . (4.12)
. (4.12)
Получим рекуррентное соотношение динамического программирования в модели управления запасами при любом k = 2, …,n.
Запишем функцию состояния (4.5) в виде
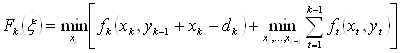 . (4.13)
. (4.13)
Здесь, как уже было сказано выше, все переменные связаны балансовыми уравнениями
![]() . (4.14)
. (4.14)
В связи с тем что величина запаса yk-1 к концу (k – 1)-го планового этапа с учетом (4.7) равна ![]() , имеем следующее рекуррентное соотношение динамической модели управления запасами:
, имеем следующее рекуррентное соотношение динамической модели управления запасами:
![]() . (4.15)
. (4.15)
Если внешних ограничений на уровни хранения и объемы производства не существует, то по аналогии с (4.11) получаем внутренние ограничения модели
![]() ,
,
![]() . (4.16)
. (4.16)
Если складские емкости и производственные мощности предприятия ограничены количеством изделий Mk и Nk соответственно, то аналогично соотношениям (4.12) имеем
![]() ,
,
![]() . (4.17)
. (4.17)
На самом деле ограничения (4.16) и (4.17) имеют более сложную структуру. Однако для решения практических задач этого вполне достаточно. Напомним лишь о том, что переменные xk и yk целочисленны и не отрицательны.
Рассмотрим теперь функцию затрат ![]() . Введем следующие обозначения:
. Введем следующие обозначения:
gt – затраты на производство и доставку заказа на t-м этапе;
ct(xt) – затраты на производство xt единиц продукции на t-м этапе;
ht(yt) – затраты на хранение yt единиц продукции в течение t-го планового этапа.
Для определенности будем считать, что производственные затраты линейны, т.е. ct(xt) = ctxt, и что затраты на хранение пропорциональны объему хранимой продукции в течении месяца. Далее, уровень (объем) хранения в течение этого месяца определяется уровнем хранения на конец этапа. Иными словами, поскольку время изготовления партий изделий пренебрежимо мало, а производить и отправлять заказчикам продукцию предприятию выгодно вначале каждого месяца, то уровень хранимого имущества в течение t-го этапа определяется соотношением баланса ![]() . В итоге получаем
. В итоге получаем ![]() .
.
Функция затрат с учетом выведенных обозначений примет вид
 (4.18)
(4.18)
Применим теперь метод динамического программирования к решению задачи управления запасами.
o Пример 6. Определение оптимальной программы производства
Рассмотрим плановый период работы предприятия, состоящий из трех месяцев: января, февраля, марта. Исходные данные сведены в таблице 1.
Таблица 1
| Этап | k | 1 | 2 | 3 |
| Месяц | Январь | Февраль | Март | |
| Спрос | dk | 2 | 5 | 2 |
| Затраты на оформление заказа | gk | 10 | 5 | 10 |
| Затраты на производство одного изделия | ck | 3 | 5 | 3 |
| Стоимость хранения одного изделия в течение месяца | hk | 2 | 2 | 1 |
Функция затрат определена формулой (4.18). Кроме того, будем считать, что предприятие не может производить более четырех изделий, а хранить – более трех, т.е. Mk = 3, Nk = 4, а уровень запасов y0 = y3 = 0.
Необходимо составить оптимальную программу выпуска продукции ![]() , которая минимизирует суммарные издержки предприятия.
, которая минимизирует суммарные издержки предприятия.
Рассмотрим январский этап (k=1). Поскольку плановый период состоит из одного месяца, у нас практически нет возможности влиять на объем производства изделий. Поэтому все допустимые программы выпуска продукции будут оптимальны, поскольку они единственны.
Функция состояния в соответствии с (4.10) примет вид
![]() .
.
Прежде чем произвести расчеты ![]() по формуле (4.18), укажем ограничения на изменения переменных x1 и y1. Поскольку уровни запасов на начало и конец планового периода равны нулю, то в январе мы можем произвести такое количество изделий, чтобы удовлетворять не только январский, но и февральский и мартовский спрос, т.е. произвести
по формуле (4.18), укажем ограничения на изменения переменных x1 и y1. Поскольку уровни запасов на начало и конец планового периода равны нулю, то в январе мы можем произвести такое количество изделий, чтобы удовлетворять не только январский, но и февральский и мартовский спрос, т.е. произвести ![]() изделий, однако N1 = 4, поэтому
изделий, однако N1 = 4, поэтому ![]() . Возникает естественный вопрос: каков должен быть уровень запасов на конец января (или, что одно и то же, на начало февраля), чтобы, не изготавливая ничего ни в феврале, ни в марте, опять выйти на нулевой уровень запасов в конце марта? Ответ очевиден: объем запасов продукции должен быть равен
. Возникает естественный вопрос: каков должен быть уровень запасов на конец января (или, что одно и то же, на начало февраля), чтобы, не изготавливая ничего ни в феврале, ни в марте, опять выйти на нулевой уровень запасов в конце марта? Ответ очевиден: объем запасов продукции должен быть равен ![]() . Но поскольку возможности склада ограничены
. Но поскольку возможности склада ограничены ![]() , в итоге получаем:
, в итоге получаем:
![]() .
.
Результаты вычислений сведем в табл. 2. ![]() .
.
Таблица 2
|
|
|
|
| 0 1 2 3 | 2 3 4 – | 10 + 3 · 2 + 1 · 0 = 16 10 + 3 · 3 + 1 · 1 = 20 10 + 3 · 4 + 1 · 2 = 24 – |
Рассмотрим k = 2, когда плановый период содержит январь и февраль. У нас появляются дополнительные возможности для изменения объема выпуска изделий на каждом из этапов, с тем чтобы выйти на ненулевой уровень запасов y3 = 0.
Рекуррентное соотношение (4.15) примем вид
![]() ,
,
где ξ – оптимальное значение уровня запасов y2 на конец второго этапа, которому соответствует наименьшие суммарные затраты на производство и хранение продукции.
Ограничения на объем производства и уровень хранения очевидны:
![]() ,
,
![]() .
.
Отобразим в таблице 3 все необходимые вычисления для февральского этапа ![]() .
.
Таблица 3
|
y2 | 0 | 1 | 2 | 3 | 4 |
|
|
| 0 | 5 – | 4 – | 3 – | 2 20 + 0 + 24 = 44 | 1 25 + 0 + 20 = 45 | 3 | 44 |
| 1 | 6 – | 5 – | 4 – | 3 – | 2 25 + 2 +24 =51 | 4 | 51 |
| 2 | 7 – | 6 – | 5 – | 4 – | 3 – | – | – |
Поясним содержание этой таблицы. Объем производства и уровень хранения определяются значениями x2 и y2 соответственно. В верхнем правом углу каждой клетки указаны уровни запасов на начало второго этапа, которые с помощью балансового уравнения вычисляются по формуле ![]() . Сумма внутри каждой клетки содержит три слагаемых. Рассмотрим эти слагаемые для клетки с координатами
. Сумма внутри каждой клетки содержит три слагаемых. Рассмотрим эти слагаемые для клетки с координатами ![]() . Первое слагаемое – затраты на оформление заказа и производство продукции
. Первое слагаемое – затраты на оформление заказа и производство продукции ![]() ; второе – затраты на хранение
; второе – затраты на хранение ![]() . Сумма двух первых слагаемых равна
. Сумма двух первых слагаемых равна ![]() . Прежде чем вычислить третье слагаемое, которое в рекуррентном соотношении обозначено как
. Прежде чем вычислить третье слагаемое, которое в рекуррентном соотношении обозначено как ![]() , вспомним, что величина
, вспомним, что величина ![]() вычислена, находится в верхнем правом углу клетки и равна 0 – 3 + 5 = 2. Поэтому третье слагаемое
вычислена, находится в верхнем правом углу клетки и равна 0 – 3 + 5 = 2. Поэтому третье слагаемое ![]() возьмем из январской таблицы. Аналогично рассчитываются слагаемые в остальных клетках, а в «запрещенных» клетках, для которых не нашлось последнего слагаемого в январской (k = 1) таблице, сделан прочерк. Наименьшие суммарные затраты
возьмем из январской таблицы. Аналогично рассчитываются слагаемые в остальных клетках, а в «запрещенных» клетках, для которых не нашлось последнего слагаемого в январской (k = 1) таблице, сделан прочерк. Наименьшие суммарные затраты ![]() для каждого y2 запишем в последнем столбце (они подсчитаны в выделенных рамкой клетках), а значения оптимальных объемов производства изделий в феврале
для каждого y2 запишем в последнем столбце (они подсчитаны в выделенных рамкой клетках), а значения оптимальных объемов производства изделий в феврале ![]() занесем в предпоследний столбец таблицы.
занесем в предпоследний столбец таблицы.
При k = 3 плановый период уже включает в себя январь, февраль и март. Запишем рекуррентное соотношение
![]() ,
,
где ξ – значения уровня запасов y3 на конец марта, которому соответствуют наименьшие суммарные затраты на хранение и производство продукции.
Новая таблица (табл. 4) содержит лишь одну строку, так как, по условию задачи, ![]() . Количество столбцов определим в соответствии с неравенством
. Количество столбцов определим в соответствии с неравенством
![]()
![]() .
.
Таблица 4
|
y3 | 0 | 1 | 2 |
|
|
| 0 | 2 – | 1 13 + 0 +51 = 64 | 0 16 + 0 + 44 =60 | 2 | 60 |
В остальном содержание таблицы ничем не отличается от предыдущей.
Составим оптимальную программу выпуска продукции на каждом этапе, которая обеспечит минимальные суммарные затраты ![]() в течение всего планового периода. Как видно из мартовской таблицы
в течение всего планового периода. Как видно из мартовской таблицы ![]() , что соответствует оптимальному уровню запасов
, что соответствует оптимальному уровню запасов ![]() , который рассчитан и записан в верхнем правом углу выделенной рамкой клетки. Далее из февральской таблицы
, который рассчитан и записан в верхнем правом углу выделенной рамкой клетки. Далее из февральской таблицы ![]() следует, что
следует, что ![]() .
.
В выделенной рамкой клетке с координатами ![]() (табл. 3) в верхнем правом углу записан оптимальный уровень запасов
(табл. 3) в верхнем правом углу записан оптимальный уровень запасов ![]() на конец января. Наконец, из январской таблицы
на конец января. Наконец, из январской таблицы ![]() получаем, что
получаем, что ![]() соответствует
соответствует ![]() . Таким образом, построена оптимальная программа выпуска продукции
. Таким образом, построена оптимальная программа выпуска продукции
![]() ,
,
![]() которая обеспечивает минимальные суммарные издержки
которая обеспечивает минимальные суммарные издержки ![]() на производство и хранение продукции.
на производство и хранение продукции.
Задачи
1. На нефтебазу бензин привозят на танкере. Накладные расходы g в расчете на партию бензина составляют 50000 руб. Ежегодно база отпускает µ = 4000 т бензина. Затраты на хранение h примем равным 0,5 руб. за 1 т бензина в сутки. Поставка осуществляется по первому требованию – мгновенно, и дефицит бензина на базе не допускается. Найдите оптимальные: объем заказываемой партии q, длительность цикла Т* работы системы и общее среднесуточные издержки ![]() .
.
Решение:
Для решения задачи используем формулы Уилсона (2.14) – (2.16). оптимальный размер заказываемой партии:
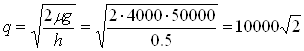 т.
т.
Интервал между заказами:
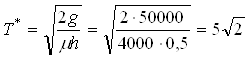 сут.
сут.
Общие среднесуточные издержки:
![]() руб./сут.
руб./сут.
2. При закупке за рубежом завода по производству электровакуумного оборудования возник вопрос о приобретении запасных частей. Комплекты запасных частей включают в себя кроме деталей и узлов, которые наиболее часто выходят из строя, приборы и электронное оборудование, обеспечивающее соблюдение технического процесса.
Стоимость хранения запасных частей и проведения профилактических работ в расчете на один комплект составляет hT = 1000 руб. В случае выхода из строя оборудования и нехватки запасных частей завод терпит убытки в размере РТ = 10000 руб. на каждый недостающий комплект оборудования. Стоимость одного комплекта запчастей с = 2000 руб. Накладные расходы при доставке оборудования составляет g= 3000 руб. Опыт эксплуатации подобных предприятий показал, что необходимое число комплектов запасного оборудования – случайная величина с рядом распределения
| Х | 0 | 1 | 2 | 3 |
| Р(Х) | 1/4 | 1/4 | 1/4 | 1/4 |
Найдите ![]() – стратегию пополнения запасов.
– стратегию пополнения запасов.
Решение:
Определим критическое число 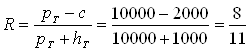 . Теперь найдем верхний уровень
. Теперь найдем верхний уровень ![]() . Функция распределения
. Функция распределения ![]() впервые превысит число R при Х = 3, следовательно
впервые превысит число R при Х = 3, следовательно ![]() .
.
Для определения ![]() найдем наименьшее значение z, для которого последний раз выполнено неравенство
найдем наименьшее значение z, для которого последний раз выполнено неравенство
![]()
(так как с = 2000). Полагаем, что все денежные суммы кратны 2000
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]() .
.
Неравенство 10000 ≤ 3000 + 1000 не выполняется, значит, ![]() .
.
Итак, ![]() . Отсюда следует, что при z < 2 запасы стоит пополнять до
. Отсюда следует, что при z < 2 запасы стоит пополнять до ![]() ; при z ≥ 2 пополнять его не нужно.
; при z ≥ 2 пополнять его не нужно.
3. В августе ежедневно из овощехранилища отгружают 50т (µ) арбузов в магазин «Овощи-фрукты». Накладные расходы в расчете на партию арбузов, доставляемых в овощехранилище, составляют g = 500 тыс. Издержки хранения скоропортящихся продуктов равны h = 5 руб. за 1 т в сутки. Партию арбузов привозят и разгружают с интенсивностью λ = 200 т/сут. Найдите оптимальный размер партии арбузов (q), привозимой в овощехранилище, периодичность Т* пополнения запасов. Определите оптимальные среднесуточные издержки ![]() , если дефицит не допускается.
, если дефицит не допускается.
4.
Решение:
Для решения задач используем формулы (2.8) – (2.10). Оптимальный размер заказываемой партии:
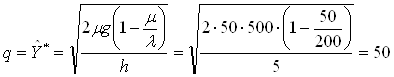 т.
т.
Периодичность пополнения запасов:
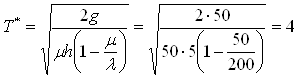 сут.
сут.
Оптимальные среднесуточные издержки:
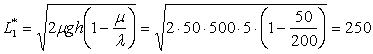 руб./сут.
руб./сут.
5. Найдите критические уровни ![]() и
и ![]() в статической модели управления запасами с вероятностным спросом и отсутствием задержек в поставках. Функции издержек хранения и дефицита линейны. Параметры задачи :hT = 6, c = 1, pT = 8, g = 2, а распределение спроса имеет вид
в статической модели управления запасами с вероятностным спросом и отсутствием задержек в поставках. Функции издержек хранения и дефицита линейны. Параметры задачи :hT = 6, c = 1, pT = 8, g = 2, а распределение спроса имеет вид
| Х | 1 | 2 | 3 | 4 | 5 |
| Р(х) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
Решение:
Определим критическое число 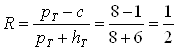 . Теперь найдем верхний уровень
. Теперь найдем верхний уровень ![]() . Функция распределения
. Функция распределения ![]() впервые превысит число R при Х = 5, следовательно
впервые превысит число R при Х = 5, следовательно ![]() .
.
Для определения ![]() найдем наименьшее значение z, для которого последний раз выполнено неравенство
найдем наименьшее значение z, для которого последний раз выполнено неравенство
![]()
(так как с = 1). Полагаем, что все денежные суммы кратны 1
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]() .
.
Вычислим ![]() :
:
![]()
Неравенство 8 < 2 + 6 не выполняется, значит, ![]() .
.
Итак, ![]() . Отсюда следует, что при z < 4 запасы стоит пополнять до
. Отсюда следует, что при z < 4 запасы стоит пополнять до ![]() ; при z ≥ 4 пополнять его не нужно.
; при z ≥ 4 пополнять его не нужно.
6. Металлургическому заводу для выплавки высоколегированной стали необходимо ежегодно µ = 100 т чугуна. Накладные расходы на запуск производства, доставку партии чугуна составляют g = 5000 руб. Хранение одной тонны чугуна в сутки обходится объединению в h = 2,5 руб. Штрафные потери за нехватку одной тонны чугуна в сутки составляют p = 50 руб. Рассчитайте оптимальный объем партии чугуна. Найдите периодичность пополнения, среднесуточные общие издержки, если поставка осуществляется мгновенно.
Решение:
Для решения задач используем формулы (2.4) – (2.6). Оптимальный объем заказываемой партии:
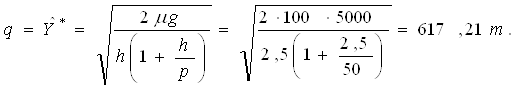
Периодичность пополнения запасов:
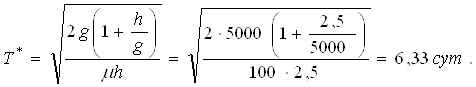
Среднесуточные общие издержки:
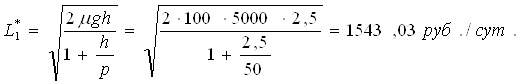
Похожие работы
... выше последний, тем больше затраты на рекламу (2,6% от торгового оборота при низких запасах и 5,7% - при высоких). У промышленных предприятии зависимость между расходами на рекламу и уровнем запасов пока вообще не прослеживается. Они еще не включили управление запасами в состав основных направлений вполне осмысленной и активно осуществляемой стратегии своего поведения в рыночной среде и явно ...
... 7. снижение потерь материальных ресур-сов при доставке и хранении; 8. уменьшение затрат на управление Глава 2. Управление запасами на примере предприятия "Стройсервис" 2.1. Краткая характеристика предприятия «Стройсервис» Общество является юридическим лицом и имеет в собственности имущество, учитываемое на ...
... руб. в год (8800 в месяц), а также экономию по налогу на имущество в размере 21120 руб в год. ЗАКЛЮЧЕНИЕ В процессе выполнения дипломной работы «Управление запасами предприятия», в соответствии с ее целью, была собрана и систематизирована информация по теоретическому обоснованию и методологии управления запасами предприятия; на основе анализа предметно-объектного материала были разработаны ...
... только свою форму, третьи - входят в изделия без каких-либо изменений, четвертые - только способствуют изготовлению изделий и не включаются в их массу или состав. 1.2 Роль и задачи анализа в управлении запасами Основными источниками контрольных данных являются первичные документы и учетные записи по счетам 10 «Материалы», 41 «Товары», 43 «Готовая продукция», а также соответствующие ...
 x2
x2 x3
x3









0 комментариев