Календарное планирование — моделирование производства во времени
Новые возможности в решении задач календарного планирования
Графики Ганта
Математический аппарат решения задач календарного планирования
Последовательные методы оптимизации
Производственная структура предприятия
Экономическая характеристика предприятия
Себестоимость и классификация затрат на производстве
Информационная модель
Экономическая эффективность
Мероприятия по борьбе с вредными и опасными факторами при работе с ПК
Навигация
Математический аппарат решения задач календарного планирования
Экономико-математическая модель оптимизации распределения трудовых ресурсов
82483
знака
8
таблиц
16
изображений
1.3 Математический аппарат решения задач календарного планирования
1.3.1 Общая характеристика задач календарного планирования
Приведенная математическая формулировка общих задач календарного планирования наглядно свидетельствует о том, что эти задачи с точки зрения математики представляют собой особый класс, возможно, совершенно незнакомый или до недавнего времени незнакомый читателю. В этих задачах мы имеем по существу дело со сложными алгебраическими структурами, дискретными процессами оптимизации, далекими от тех непрерывных процессов и функций, которые до недавнего времени, в основном, и изучались математикой.
Уже первые попытки математического решения задач календарного планирования показали, что для такого рода задач нужна, можно сказать, «новая математика» и что задачи подобного рода, по-видимому, в ближайшее время во многом изменят содержание самой математики.
Точные методы, хотя бы принципиально решающие общие задачи календарного планирования, получены только в самое последнее время. Однако, как мы увидим дальше, эти точные методы, хотя и представляют значительный интерес при построении общей теории оптимальных решений, в настоящее время могут принести мало практической пользы в производственном управлении, настолько велики объемы вычислений для решения этими методами мало-мальски реальных задач производственного планирования. Только в самых простых случаях относительно легко удается с уверенностью получить точное решение задачи.
Наряду с разработкой точных методов совершенствуются различные методы и подходы приближенного решения задач календарного планирования. Это направление в настоящее время является практически наиболее продуктивным. Оно заслуживает наибольшего внимания с точки зрения общей теории решения задач календарного планирования, а также полезно и для улучшения вычислительных схем точного решения задач. В частности, различные эффективные эвристические приемы поиска близких к оптимальному решений, как правило, могут быть использованы и в процессе конструирования точного решения задачи. Точно так же, более глубокое понимание процесса конструирования точного решения задачи может подсказать эффективные приемы поиска решений, близких к оптимальному.
Кроме этого в решении задач календарного планирования оказываются эффективными различного рода методы моделирования, в том числе основанные на применении схем статистических испытаний — методов Монте-Карло. Хотя в настоящее время еще и нет разработанной приемлемой теории такого рода методов, однако их практическая эффективность свидетельствует о возможности построения такого рода теорий.
Математические методы решения задач календарного планирования разрабатываются в рамках бурно развивающейся в последние годы математической теории расписаний.
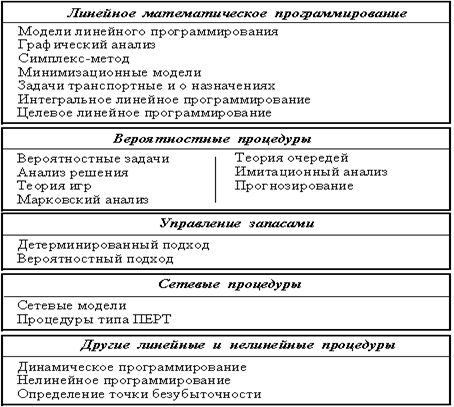
В настоящее время нельзя остановиться на каком-то одном классе методов решения задач календарного планирования. Для одних задач исключительно эффективны методы динамического программирования или их дальнейшее развитие — методы последовательного конструирования, анализа и отбора вариантов, другие задачи могут решаться методами моделирования; некоторые задачи могут быть успешно решены ставшими уже классическими методами линейного программирования.
1.3.2 Модели линейного программирования
Попытки решить некоторый новый класс задач с помощью уже известных методов довольно естественны, поэтому неудивительно, что многие исследователи пытаются решать задачи календарного планирования с помощью получивших широкую известность и распространение методов линейного программирования. К схемам линейного программирования сводятся многие задачи, имеющие непосредственное отношение к оперативному планированию — такие, как задачи загрузки оборудования, задачи распределения заказов и др.
Как известно, линейное программирование охватывает совокупность методов решения задач минимизации (максимизации) линейных функций при линейных ограничениях па неизвестные — равенствах или неравенствах. Математический аппарат решения задач линейного программирования достаточно хорошо разработан. В последние годы предложены методы решения задач так называемого линейного целочисленного программирования, когда помимо всего требуется, чтобы неизвестные принимали только целочисленные значения. Эти успехи линейного программирования вызвали многочисленные попытки решения задач календарного планирования при помощи линейного программирования.
Такого рода попытки, понятно, привели к необходимости несколько перестроить математическую формулировку задач календарного планирования. В частности, один из создателей теории линейного программирования Дж. Данциг предложил следующую постановку задачи календарного планирования.
На основании практических соображений иногда можно указать некоторые возможные варианты графиков обработки каждой детали — изолированно построить несколько таких вариантов (этот процесс, естественно, может быть автоматизирован). Затем из этих вариантов ищется наиболее подходящая «смесь», подобно тому, как ищется наилучший рацион питания в «задачах диеты», или же определяется наилучшая смесь ингредиентов для получения высококачественных сортов бензина.
Данциг поясняет эту идею на таком примере.
Пусть имеются две детали 
и d2, в каждой из которых по две операции. Время обработки каждой операции равно единице, маршруты деталей следующие:
Иными словами, первая операция детали d1 обрабатывается на первом рабочем месте R1 вторая операция детали d1 и первая операция детали d2 обрабатываются на R2, вторая операция d2 обрабатывается на R3.
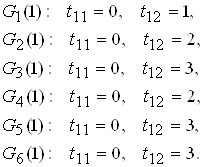
Данциг рассматривал по шесть (возможных) изолированно построенных вариантов обработок первой и второй детали, ориентируясь на работу в четыре последовательных периода, каждый из которых равен единице времени.
В этом случае первая деталь может обрабатываться одним из следующих способов:
Введем неизвестные 
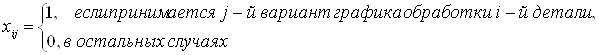
Тогда, очевидно, для нашей задачи
.
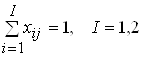По каждому рабочему месту Rk, по каждому из четырех рассматриваемых периодов (напомним, каждый период равен единице) необходимо выполнение соотношения, равносильного требованию, чтобы на рабочем месте одновременно не могли выполняться две операции
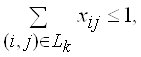
где 
- начало периода.
Для рассматриваемого примера эти условия могут быть записаны в стандартной форме (табл. 1.2).
В качестве критерия оптимальности выбрана линейная функция, которая равна нулю, если ни одна работа не выполняется в 4-й период.
Таблица 1.2
Условия для задачи
|
| Периоды |
|
|
|
|
|
|
|
|
|
|
|
| |
| 1 | 1 2 3 | 1 | 1 | 1 | 1 | 1 | 1 | ≤1 ≤1 ≤1 | ||||||
| 2 | 1 2 3 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ≤1 ≤1 ≤1 |
| 3 | 2 3 4 | 1 | 1 | 1 | 1 | 1 | 1 | ≤1 ≤1 ≤1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | min |
Уже в данной формуле естественно возникает необходимость в получении целочисленного решения. Различными исследователями указаны способы сведения к задачам целочисленного линейного программирования и более общих задач календарного планирования. Однако для всех этих схем присущ общий недостаток — такое сведение приводит к задачам линейного программирования очень большого объема, в чем можно убедиться уже на примере Данцига. Для примера Данцига более эффективной схемой решения по сравнению с методами линейного программирования оказывается простая схема перебора всех возможных вариантов. Хорошо известно также, что в настоящее время мы пока не располагаем более-менее приемлемыми методами решения задач целочисленного линейного программирования. Так что на этом пути не были получены сколько-нибудь заслуживающие внимания методы решения задач календарного планирования, хотя решение отдельных примеров и было продемонстрировано.
Такое положение, на наш взгляд, не случайно. Насильственное «втискивание» ярко выраженных комбинаторных дискретных задач в схемы линейного программирования вызывает увеличение объемов задач, что, понятно, не может вы сказаться на времени их решения. Уже в модели Данцига для того, чтобы быть уверенным, что получено оптимальное (или близкое к оптимальному) решение, в рассмотрение следует ввести довольно большое количество изолированно построенных графиков каждой детали, что также ведет к увеличению размерности задачи. Уменьшение числа возможных вариантов графиков не позволяет надеяться на оптимальность решения.
Похожие работы
... z = х47 - х45 -> шах. Глава 2. Определение структурных сдвигов и эффективности оптимального плана 2.1 Анализ оптимального решения экономико-математической модели оптимизации производственной структуры сельскохозяйственного предприятия Экономикс - математический анализ представляет собой заключительный этап математического моделирования экономических процессов, который основывается на ...
... Теория очередей 59,7 Нелинейное программирование 46,8 Динамическое программирование 38,7 Теория игр 30,6 Следует отметить определенную переоценку значимости экономико-математических моделей в реальной практике управления экономико-производственными системами. Это связано с непреодолимыми пока сложностями моделирования процессов в экономико-производственных системах из-за непрерывности ...
... вариант программы позволит работать с единой информационной базой с нескольких рабочих мест. Система также содержит средства обеспечения сохранности и непротиворечивости информации. Для того чтобы ориентировочно оценить, во что может обойтись компании автоматизация управления персоналом, следует обратиться к таблице 1.1. Таблица 1.1 - Внедрение, соотношение затрат и стоимостные оценки ...
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
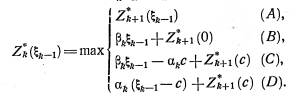
0 комментариев