Навигация
Показатели динамики себестоимости продукции
5.2 Показатели динамики себестоимости продукции
Построим ряд динамики абсолютных значений себестоимости единицы продукции по кварталам, то есть применим метод укрупнения интервалов. Преобразованные ряды динамики из суммарных величин лучше выражают тенденции себестоимости. Исходные данные и полученные результаты приведены в приложении Б.
Показатели ряда динамики рассчитываются следующим образом:
Абсолютный прирост определяется как разность уровней ряда и выражается в единицах измерения показателей ряда. Различают цепные и базисные показатели. Цепные – когда уровни сравниваются с уровнем предыдущего периода, а базисные – уровень сравнивается с уровнем принятым за базу.
- цепной![]() ;
;
- базисный (накопленный)![]() ;
;
где![]() ,
, ![]() – начальный уровень ряда динамики и уровень себестоимости единицы продукции в i-м квартале.
– начальный уровень ряда динамики и уровень себестоимости единицы продукции в i-м квартале.
В 5 квартале наблюдалось понижение себестоимости и по сравнению с предыдущим кварталом, и по сравнению с первым.
Темпы роста – это отношение уровней ряда одного периода к другому. Они показывают как изменился показатель.
- цепной 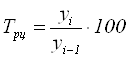 ;
;
- базисный 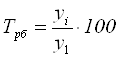 .
.
Темпы прироста дают относительную оценку значения абсолютного прироста по сравнению с первоначальным уровнем; показывают на сколько процентов увеличились размеры явлений за изучаемый период времени.
- цепной 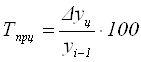 или
или ![]() ;
;
- базисный 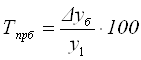 или
или ![]() .
.
Показатель абсолютного значения 1% прироста служит оценкой значимости веса 1% прироста. Он равен частному от деления абсолютного прироста за определенный период на темп прироста за тот же период, выраженный в процентах.
Произведем расчет средних показателей ряда динамики:
- средний абсолютный прирост
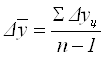 = 0,9 руб.
= 0,9 руб.
То есть в среднем за квартал себестоимость увеличивалась на 0,9 руб.
- при анализе развития явления часто возникает потребность дать обобщенную характеристику интенсивности развития за длительный период. Определяем средние темпы роста как средние геометрические:
![]() = 100,14%
= 100,14%
Это означает, что в среднем за квартал себестоимость увеличилась в 1 раз.
- средний темп пророста
![]() = 0,14%
= 0,14%
где m – число коэффициентов роста; n – число уровней ряда динамики.
То есть в среднем за квартал себестоимость росла на 0,14%.
Таким образом, по абсолютным приростам и темпам роста можно сделать вывод, что себестоимость продукции по кварталам изменялась скачкообразно. Темпы прироста за рассматриваемый период тоже различны: имеются как положительные, так и отрицательные значения. По средним показателям ряда можно сказать, что за весь наблюдаемый период (2 года) наблюдается повышение себестоимости.
5.3 Выявление основной тенденции ряда динамики себестоимости продукции
Выявление основной тенденции развития является важной задачей при анализе рядов динамики. В некоторых случаях общая тенденция развития объекта ясно отображается уровнями ряда динамики, например, когда наблюдается систематическое снижение или рост уровней ряда. В других случаях уровни ряда претерпевают различные изменения и можно говорить лишь об общей тенденции.
Построим ряд динамики помесячных значений себестоимости единицы продукции. За колебаниями ежемесячных значений может не просматриваться общая тенденция динамики, поэтому для её выявления воспользуемся следующими статистическими методами:
- Укрупнение интервалов. Рассматриваемый период разобьем на 8 интервалов – кварталов. Укрупненные кварталы представлены в приложении В. Построим 2 графика по помесячным значениям себестоимости и по укрупненным интервалам.
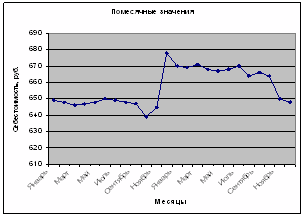
Рис. 5.1. Значения себестоимости по месяцам
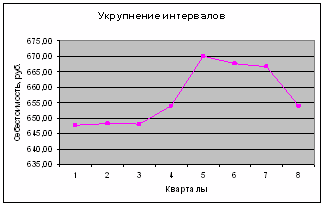
Рис. 5.2. Значения себестоимости по кварталам
Укрупнив интервалы с помесячными значениями, получили более усредненную линию значений, которая отражает не только основную тенденцию, но и то, что в 5 квартале каждого года наблюдается понижение себестоимости по сравнению с другими кварталами.
- Метод скользящей средней. Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
Интервал скольжения может быть нечетный (5,7,…) и четный (4,6,…). Нахождение скользящей средней по четному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, т.е. расчет средней из двух промежуточных сумм.
Интервал скольжения возьмем 5. Результаты вычислений представим в таблице 5.1.
Таблица 5.1.Скользящие средние значения себестоимости единицы продукции
| Год, месяцы | Себестоимость единицы продукции, тыс. руб. | Пятимесячные скользящие суммы | Пятимесячные скользящие средние |
| Январь | 649 | ||
| Февраль | 648 | ||
| Март | 646 | 647,6 | |
| Апрель | 647 | 647,8 | |
| Май | 648 | 3238 | 648 |
| Июнь | 650 | 3239 | 648,4 |
| Июль | 649 | 3240 | 648,4 |
| Август | 648 | 3242 | 646,6 |
| Сентябрь | 647 | 3242 | 645,6 |
| Октябрь | 639 | 3233 | 651,4 |
| Ноябрь | 645 | 3228 | 655,8 |
| Декабрь | 678 | 3257 | 660,2 |
| Январь | 670 | 3279 | 666,6 |
| Февраль | 669 | 3301 | 671,2 |
| Март | 671 | 3333 | 669 |
| Апрель | 668 | 3356 | 668,6 |
| Май | 667 | 3345 | 668,8 |
| Июнь | 668 | 3343 | 667,4 |
| Июль | 670 | 3344 | 667 |
| Август | 664 | 3337 | 666,4 |
| Сентябрь | 666 | 3335 | 662,8 |
| Октябрь | 664 | 3332 | 658,4 |
| Ноябрь | 650 | 3314 | |
| Декабрь | 648 | 3292 |
Данную таблицу используем для построения графиков по месячным значениям себестоимости и по методу скользящей средней, представим графики на рис. 5.3.
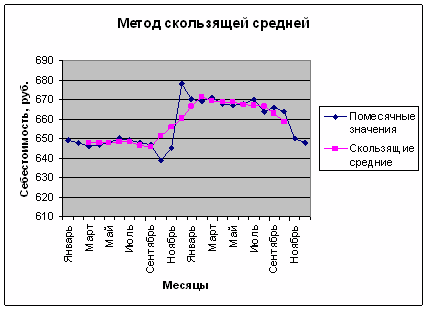
Рис. 5.3. Метод скользящей средней
Данный метод приводит к аналогичным выводам об общей тенденции себестоимости к повышению и об ее понижении в пятом квартале.
- Аналитическое выравнивание. Является наиболее эффективным способом выявления основной тенденции динамики и может быть осуществлено по любому рациональному многочлену. Для выравнивания ряда динамики по прямой воспользуемся следующим уравнением:
![]() .
.
Для нахождения параметров ![]() и
и ![]() по методу наименьших квадратов строится система нормальных уравнений:
по методу наименьших квадратов строится система нормальных уравнений:
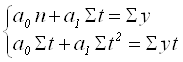
Где у – исходные уровни ряда динамики;
n – количество членов ряда;
t – показатель времени, который обозначается порядковыми номерами.
Зададим значения t таким образом, чтобы ![]() , тогда система уравнений примет вид:
, тогда система уравнений примет вид:
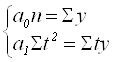 ,
,
Результаты вычислений представлены в таблице П 3. Тогда можно вычислить:
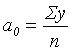 = 657,04,
= 657,04, 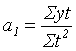 = 0,81.
= 0,81.
Таким образом, уравнение имеет вид:
![]() =657,04 + 0,81t
=657,04 + 0,81t
Построим в одних осях прямую, описываемую данным уравнением и кривую фактических значений, представим это на рис.5.4.
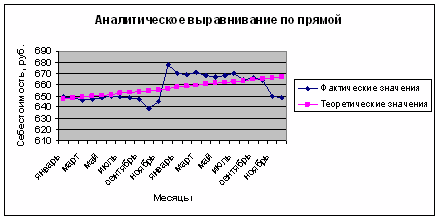
Рис. 5.4. Аналитическое выравнивание по прямой
Данный рисунок подтверждает общую тенденцию к повышению себестоимости.
Построив уравнение динамики, проведем оценку его надежности, используя критерий Фишера:
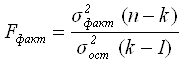 = 163,8
= 163,8
где![]() – факторная дисперсия,
– факторная дисперсия, 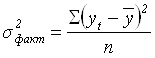 = 657,04
= 657,04
![]() – остаточная дисперсия,
– остаточная дисперсия, 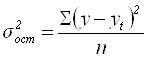 = 88,24
= 88,24
![]() – число параметров уравнения, описывающего основную тенденцию (для уравнения прямой
– число параметров уравнения, описывающего основную тенденцию (для уравнения прямой ![]() ).
).
Сравним фактический критерий Фишера с теоретическим (табличным) значением, которое равно при α = 0,05 19, α = 0,01 99.
Так как фактический критерий Фишера меньше, то построенная модель неадекватна фактической временной тенденции.
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики. Колеблемость уровней ряда около тренда служит мерой воздействия остаточных факторов. Ее можно найти по формуле среднего квадратического отклонения:
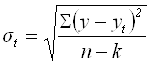 = 9,81 тыс. руб.
= 9,81 тыс. руб.
Относительной мерой колеблемости уровней эмпирического ряда относительно тренда является коэффициент вариации:
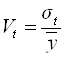 = 0,014933
= 0,014933
Колеблемость от линии тренда составляет 9,81 руб. или 1,4%. Так как коэффициент вариации меньше 30%, то значения уровней ряда достаточно однородны.
Используя уравнение динамики, выполним экстраполяцию себестоимости единицы продукции на следующий временной период. Экстраполяция – нахождение уровней за пределами изучаемого ряда, т.е. продление ряда на основе выявленной закономерности изменения уровней в изучаемый отрезок времени.
Можно использовать следующие методы экстраполяции:
– на основе средних характеристик данного ряда динамики: среднего абсолютного прироста и среднего темпа роста;
– аналитическое выравнивание ряда, при этом достаточно продолжить значение независимой переменной – времени.
Воспользуемся вторым методом. Для этого возьмем значение t =13, для которого себестоимость равна 667,62.
При составлении прогноза оперируют интервальной оценкой, определяя доверительные интервалы прогноза. Величина доверительного интервала определяется:
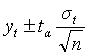 =
= ![]() ± 4,15 при
± 4,15 при ![]() =0,05
=0,05
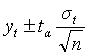 =
= ![]() ± 5,64 при
± 5,64 при ![]() = 0,01
= 0,01
где![]() – среднее квадратическое отклонение от тренда;
– среднее квадратическое отклонение от тренда;
![]() – табличное значение t-критерия Стьюдента при уровне значимости
– табличное значение t-критерия Стьюдента при уровне значимости ![]() .
.
![]() при
при ![]() =0,05 равен 2,074, при 0,01 – 2,819.
=0,05 равен 2,074, при 0,01 – 2,819.
Из величины доверительного интервала при ![]() =0,05 можно сделать вывод, что при t =13 себестоимость будет находиться в интервале от 663,47 до 673,26 руб.
=0,05 можно сделать вывод, что при t =13 себестоимость будет находиться в интервале от 663,47 до 673,26 руб.
Похожие работы
... на создание современных производств комплектующих изделий, но затем идут и на организацию выпуска готовой мебели. Такую стратегию проводит шведский концерн «Икея», планирующий вложить в мебельную промышленность Северо-Запада России более 100 млн. евро. Концерн учредил компанию «Икея-Россия», которая уже построила в городе Тихвине Ленинградской области завод по производству комплектующих для ...
0 комментариев