Навигация
Оценка влияния факторов методом аналитической группировки
6.2 Оценка влияния факторов методом аналитической группировки
На этапе обоснования модели при построении аналитической группировки решается задача определения числа групп и границ интервалов. При равных интервалах целесообразно увеличивать число групп до тех пор, пока линия групповых средних сохраняет плавный характер и существенно не искажается случайными скачками. Построим аналитическую группировку.
В качестве факторного признака воспользуемся количеством продукции. Возьмем 5 разных по длине интервалов с равным количеством наблюдений. Представим результаты вычислений в таблице 6.2.
Таблица 6.2 Аналитическая группировка себестоимости единицы продукции по производительности
| Группы по факторному признаку | Среднее значение | Численность, | |
| 54-119 | 648,71 | 7 | |
| 120-185 | 648,17 | 6 | |
| 186-251 | 667,33 | 6 | |
| 252-317 | 666,50 | 2 | |
| 318-… | 667,33 | 3 |
Построим график групповых средних совместно с соответствующей эмпирической линией:
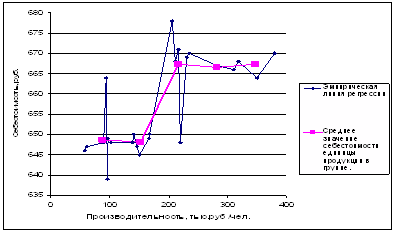
Рис. 6.3 - Аналитическая группировка по производительности
Методика измерения тесноты связи в аналитической группировке вытекает из правила сложения дисперсий:
![]() .
.
Общая дисперсия ![]() характеризует вариацию результативного признака (у) от всех влияющих на него факторных признаков:
характеризует вариацию результативного признака (у) от всех влияющих на него факторных признаков:
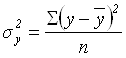 или
или ![]() ,
,
где n – численность совокупности.
Групповые дисперсии ![]() и средняя из групповых
и средняя из групповых ![]() характеризуют вариацию результативного признака у от всех факторных признаков, кроме признака х, по которому построена группировка:
характеризуют вариацию результативного признака у от всех факторных признаков, кроме признака х, по которому построена группировка:
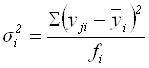 ;
;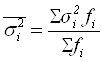 ,
,
гдеj – порядковый номер значения признака в i-й группе.
Межгрупповая дисперсия ![]() характеризует вариацию результативного признака от признака, положенного в основание группировки:
характеризует вариацию результативного признака от признака, положенного в основание группировки:
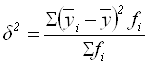 .
.
Отсюда можно получить относительный показатель – дисперсионное отношение – показывающий удельный вес вариации, связанной с группировочным признаком в общей дисперсии:
 .
.
Тесноту связи характеризует эмпирическое корреляционное отношение:
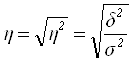 ;
; ![]() ,
, ![]() – связь слабая.
– связь слабая.
![]() – связь тесная.
– связь тесная.
Определив тесноту связи, необходимо убедиться, что связь эта не случайна, т.е. провести проверку существенности связи. Для этой цели может быть использован критерий Фишера (F – критерий):
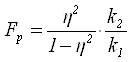 или
или 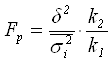 ,
,
![]() ,
, ![]() ,
,
где ![]() – расчетное значение критерия Фишера;
– расчетное значение критерия Фишера;
n – число единиц совокупности;
m – количество групп.
Если ![]() , то существенность связи подтверждается, где
, то существенность связи подтверждается, где ![]() – критическое значение критерия Фишера, которое находится по таблицам.
– критическое значение критерия Фишера, которое находится по таблицам.
Результаты расчетов по двум аналитическим группировкам ведем таблицу 6.4.:
Таблица 6.4 Расчет показателей по аналитическим группировкам
| Расчитанные показатели | Номер интервала | Аналитическая группировка |
| Среднее значение ряда распределения | 175,3089619 | |
| Внутригрупповая дисперсия | 1 | 47,03 |
| 2 | 190,01 | |
| 3 | 81,40 | |
| 4 | 0,94 | |
| 5 | 6,22 | |
| Дисперсия средняя из групповых | 82,43 | |
| Межгрупповая дисперсия | 87,09 | |
| Общая дисперсия | 169,52 | |
| Дисперсионное отношение | 0,51 | |
| Эмпирическое корреляционное отношение | 0,72 | |
| К1 | 4 | |
| К2 | 19 | |
| к2/ к1 | 5,02 | |
| при α 0,05 | 2,9 | |
| при α 0,01 | 4,5 |
Из полученных данных видно, что при производительности труда рабочих в качестве факторного признака η = 0,72 а это близко к 0,76, значит связь тесная. Таким образом, на результативный признак оказывает влияние производительность труда работников. Этот признак будем использовать в дальнейших исследованиях.
Похожие работы
... на создание современных производств комплектующих изделий, но затем идут и на организацию выпуска готовой мебели. Такую стратегию проводит шведский концерн «Икея», планирующий вложить в мебельную промышленность Северо-Запада России более 100 млн. евро. Концерн учредил компанию «Икея-Россия», которая уже построила в городе Тихвине Ленинградской области завод по производству комплектующих для ...
0 комментариев