Навигация
Простое вариационное преобразование
1. Простое вариационное преобразование
jD: M=<x,f> ÛMD=<Dx,s>
включает преобразование исходных величин и преобразование их отношений.
а) преобразование исходных величин состоит в переходе от исходных величин к их простым вариациям и включает
jD: xÛDx, где
Dx(Dt)=x(t)-x0(t0) - уравнение простой вариации;
x(t) - состояние исходной величины в текущий момент времени t;
x0(t0) - состояние исходной величины в исходный момент времени t;
Dx(Dt) - простая вариация, определяемая как изменение исходной величины за интервал времени Dt=t-t0.
б) преобразование отношений состоит в переходе от отношений исходных величин к их простым чувствительностям
jD: f Ûs., где s(j,i) - простая чувствительность, которая определяется как отношение приращения Dxjj-ой исходной величины к вызывающему его приращению Dxii-ой исходной величины;
s(xj, xi)=Dxj /Dxi- уравнение простой чувствительности в форме изменений.
s(xj, xi)=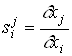 - дифференциальная форма простой чувствительности.
- дифференциальная форма простой чувствительности.
2. Относительное вариационное преобразование
jD: M=<x,f> Û Md=<dx,S>
включает преобразование исходных величин и преобразование их отношений.
а) преобразование исходных величин состоит в переходе от исходных величин к их относительным вариациям
jD: xÛdx, где
dx(Dt)=Dx(Dt)/x0(t0) - уравнение относительной вариации;
x0(t0) - состояние исходной величины в исходный момент времени t;
Dx(Dt) - простая вариация,
dx(Dt) - относительная вариация, определяемая как отношение простой вариации за интервал времени Dt=t-t0 x0(t0) к состоянию исходной величины в исходный момент времени t;
б) преобразование отношений состоит в переходе от отношений исходных величин к их относительным чувствительностям
jD: fÛS., где S(j,i) - относительная чувствительность, которая определяется как отношение относительного приращения dxjj-ой исходной величины к вызывающему его относительному приращению dxii-ой исходной величины;
S(xj, xi)= dxj/dxi- уравнение относительной чувствительности в форме изменений.
S(xj,xi)=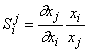 - дифференциальная форма относительной чувствительности
- дифференциальная форма относительной чувствительности
Относительные чувствительности также называют логарифмическими, поскольку
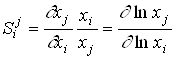
Для описания и анализа продукционной системы применим аппарат теории чувствительности. Важное место в теории чувствительности занимают инварианты, при помощи которых устанавливают функционально полный набор величин для описания динамических моделей. Равенство нулю полных сумм чувствительностей позволяет определить минимально необходимый и функционально достаточный для анализа набор рентабельностей и финансовых коэффициентов. Такой ограниченный, но полный набор величин обосновывает существенное сокращение размерности адекватных описаний экономических объектов.
Параметрическими относительными чувствительностями называют весовые коэффициенты, которые определяют оператором ![]() вида
вида ![]() =dxj /dxi, где индес j принимает значения j=1,2,…,I. Дифференциальная форма относительных чувствительностей задается выражением
=dxj /dxi, где индес j принимает значения j=1,2,…,I. Дифференциальная форма относительных чувствительностей задается выражением
|
|
Утверждение 1. Продукционная система представима уравнениями сохранения стоимости продукта и продуцента:
| z=x+y, | (1а) |
| Z=X+Y. | (1б) |
Утверждение 2. Пусть продукт и продуцент описываются уравнениями сохранения стоимости (1). Тогда полные алгебраические суммы значений послойных элементов продукта и продуцента тождественно равны нулю и описываются топологическими уравнениями:
|
|
|
| (2а) |
|
|
|
| (2б) |
Утверждение 3. Пусть продукционная система описывается топологическими уравнениями (1). Тогда для i–ого элемента продукта и продуцента справедливы уравнения связи между слоями, которые описываются уравнениями сохранения и акселерации стоимости для всех i=1,2,…,I
| zi=xi+yi. | Zi=Xi+Yi | (3а) |
| yi=aiziDt | Yi =biZiDt | (3б) |
где a, b - показатели акселерации стоимости продукта и продуцента в процессе циркуляции.
Уравнения сохранения и акселерации стоимости (3) образуют функции продуцирования продукционной системы, которые являются аналогом производственной функции производителя.
Утверждение 4. Поведение продукционной системы описывается послойными уравнениями переходов (изменений состояний за время Dt) элементов продукта и продуцента из начального состояния в конечное.
Пусть послойные уравнения переходов элементов продукта описывают поведение продукта
| xi(t0+Dt)=xi(t0)+Dxi(Dt) | (4а) |
| yi(t0+Dt)=yi(t0)+Dyi(Dt) | (4б) |
| zi(t0+Dt)=zi(t0)+Dzi(Dt) | (4в) |
Пусть послойные уравнения переходов элементов продуцента описывают поведение продуцента
| Xi(t0+Dt)=Xi(t0)+DXi(Dt) | (5а) |
| Yi(t0+Dt)=Yi(t0)+DYi(Dt) | (5б) |
| Zi(t0+Dt)=Zi(t0)+DZi(Dt) | (5в) |
Тогда послойные уравнения переходов элементов продукта и продуцента (4), (5) связаны отношениями:
присваивания дополнительной стоимости
| yi(t0)=Yi(t0) | (6а) |
капитализации присвоенной дополнительной стоимости
| Xm=Ym, | (6б) |
где m – индекс собственного капитала, mÎI.
Утверждение 5. Пусть продукционная система описывается послойными топологическими уравнениями (3) и уравнениями (4) и (5) переходов за время Dt. Тогда полные суммы простых изменений послойных элементов продукта и продуцента тождественно равны нулю
|
|
|
| (7а) |
|
|
|
| (7б) |
Утверждение 6. Рассмотрим полные суммы относительных изменений, описываемых оператором d вида dx=Dx/x0.
Пусть продукционная система описывается послойными уравнениями (7) нулевых сумм простых изменений.
Тогда полные суммы относительных изменений элементов продукта и продуцента тождественно равны нулю
|
|
|
| (8а) |
|
|
|
| (8б) |
Утверждение 7. К относительным чувствительностям применим принцип инвариантности, который состоит в том, что полная сумма относительных чувствительностей тождественно равна нулю.
Пусть продукционная система описывается послойными уравнениями (8) нулевых сумм относительных изменений.
Тогда полные суммы относительных чувствительностей элементов продукта и продуцента тождественно равны нулю
|
|
|
| (9а) |
|
|
|
| (9б) |
Утверждение 8. Принцип инвариантности относительных чувствительностей устанавливает также тождественное равенство нулю двойных полных сумм относительных чувствительностей.
Пусть продукционная система описывается послойными уравнениями (9) нулевых сумм относительных чувствительностей.
Тогда двойные полные суммы относительных чувствительностей послойных элементов продукта и продуцента тождественно равны нулю
|
|
|
| (10а) |
|
|
|
| (10б) |
Двойные полные суммы относительных чувствительностей (10) описываются матрицей чувствительностей ![]() , для компонентов которой справедливы утверждения:
, для компонентов которой справедливы утверждения:
· диагональные компоненты тождественно равны единице, ![]() ;
;
· кососимметричные компоненты взаимнообратны, ![]() .
.
Значимость относительных чувствительностей состоит в том, что они описывают величины, называемые в экономическом анализе «финансовыми коэффициентами». Учитывая, что основное балансовое уравнение и топологические уравнения (3) имеют аддитивный характер, то ![]() и значения относительных чувствительностей сводятся к отношениям вида
и значения относительных чувствительностей сводятся к отношениям вида
|
| (11а) |
Таким образом, матрицы чувствительности ![]() задают полные матрицы финансовых коэффициентов.
задают полные матрицы финансовых коэффициентов.
Для основной стоимости элементы матрицы финансовых коэффициентов имеют вид
|
|
| (11б) |
Запишем полную матрицу финансовых коэффициентов для продукционной системы представленной послойными уравнениями стоимости продуцента и продукта в форме бизнес-компонента.
| Модель продуцента | Модель продукта | |
| Уравнение основной стоимости | X11+X12=X21+X22 | x11+x12=x22 |
| Уравнение дополнительной стоимости | Y11+Y 12=Y22 | y11+y12=y22 |
| Уравнение полной стоимости | Z11+Z12=Z21+Z22 | z11+z12=z22 |
В формулах продуцента и продукта использованы следующие элементы:
а) элементы баланса капитала (форма1)
· X22 - инвестированный капитал
· X21 - резервный капитал
· X12 - заемный капитал
· X11 - собственный капитал
б) элементы баланса прибыли/убытки (форма2)
· Y22 – валовый доход от инвестиций
· Y12 – плата за заемный капитал
· Y11 – прибыль
Полные матрицы финансовых коэффициентов для продукта и продуцента имеют вид
|
|
| (11в) |
Учитывая, что ![]() , матрицы коэффициентов можно считать кососимметричными.
, матрицы коэффициентов можно считать кососимметричными.
Умножая матрицы коэффициентов на единичный вектор, получим полные системы уравнений финансовых коэффициентов для продукта и продуцента:
в матричной форме
|
|
| (11г) |
в алгебраической форме
|
|
| (11д) |
Аналогичный вид имеют матрицы финансовых коэффициентов для слоев дополнительной стоимости.
Утверждение 9. Определим основные соотношения чувствительностей, входящими в описания продукта и продуцента. Отношение дополнительной стоимости, полученной за некоторый период времени Dt, к основной или полной, называют “рентабельностью”.
Пусть определены следующие виды рентабельности:
· mi(xi)=yi/xi, mi(zi)=yi/zi - основная и полная рентабельность продукта;
· gi(Xi)=Yi/Xi, gi(Zi)=Yi/Zi - основная и полная рентабельность капитала продуцента.
Тогда рентабельности продуцента и продукта связаны соотношениями типа формул Дюпона
| gi(Xi)=mi(xi)N(xi), | gi(Zi)=mi(zi)N(zi), | (12) |
где N(xi)=xi/Xi, N(zi)=zi/Zi– оборачиваемость капитала продуцента в стоимости продукции.
Утверждение 10. Пусть продукционная система описывается уравнениями (9) нулевых сумм относительных чувствительностей.
Тогда полные суммы рентабельностей продукта и продуцента, взвешенных по чувствительностям, тождественно равны нулю
|
|
| (13а) |
|
|
| (13б) |
Переходя к финансовым коэффициентам (11) запишем уравнения взвешенных рентабельностей
|
|
| (13в) |
Полные системы уравнений основной рентабельности в матричной форме
|
|
| (13г) |
Полные системы уравнений основной рентабельности в алгебраической форме
|
|
| (13д) |
Пример. Рассмотрим уравнение для рентабельности собственного капитала (13д), в котором положим g21=0
![]() .
.
Из уравнения для финансовых коэффициентов (11д) определим коэффициент инвестиций
![]() .
.
Перепишем уравнение для рентабельности собственного капитала
![]() .
.
Группируя члены относительно финансовых коэффициентов, получим известную формулу «финансовый рычаг»
![]() .
.
Пример.
Полные суммы относительных изменений элементов продукта и продуцента тождественно равны нулю (8).
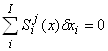
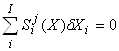
Полные системы уравнений относительных изменений в матричной форме
|
|
| (13г) |
Полные системы уравнений относительных изменений в алгебраической форме
|
| (13д) |
|
| (13д) |
Первое уравнение относительных изменений перепишем в виде
|
| (13д) |
Из уравнения для финансовых коэффициентов (11д) определим коэффициент инвестиций
![]() .
.
Подставляя коэффициент инвестиций перепишем уравнение относительных изменений в виде
|
| (13д) |
Упорядочивая слагаемые по финансовым коэффициентам получим
|
| (13д) |
Похожие работы
... ). К оптимальным точным можно отнести методы теории оптимальных процессов, некоторые методы математического программирования и методы исследования операций, к оптимизационным приближенным - часть методов математического программирования, исследования операций, экономической кибернетики, эвристические. К не оптимизационным точным принадлежат методы элементарной математики и классические методы ...
... более сложных систем с целью познания происходящих в них процессов - воспроизводства жизни, обучения и так далее. Наиболее известно техническое значение кибернетики - создание на основе кибернетических принципов ЭВМ, роботов, ПЭВМ, породившее тенденцию кибернетизации и информатизации не только научного познания, но и ...
... Кибернетика сегодня КИБЕРНЕТИКА (греч. — искусство управления) - наука об управлении, получении, передаче и преобразовании информации в кибернетических системах. Непосредственной предшественницей кибернетики была теория автоматического управления, рассматривающая относительно простые объекты и управляющие системы, описываемые системами дифференциальных и разностных уравнений. С появлением ...
... цель исследования, указать ограничения , поставить основные вопросы на которые мы хотим получить ответы в результате решения задачи. Здесь следует выделить наиболее существенные черты экономического объекта, важнейшие зависимости, которые мы хотим учесть при построении модели. Формируются некоторые гипотезы развития объекта исследования, изучаются выделенные зависимости и соотношения. Когда ...
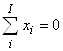
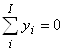
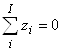
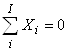
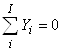
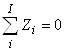
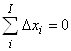
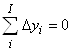
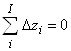
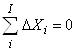
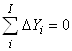
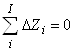
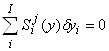
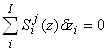
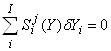


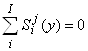

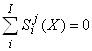
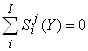

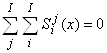
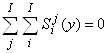
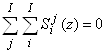

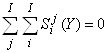

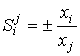 .
.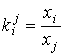 ,
,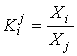 .
. ,
, .
. ,
, .
. ,
,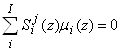 .
. ,
,
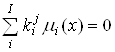 ,
, .
. ,
, .
. ,
, .
.
0 комментариев