Особенности применения дидактических игр при обобщении знаний учащихся

2.4. Особенности применения дидактических игр при обобщении знаний учащихся

На этапе обобщения знаний целесообразно проводить уроки в форме путешествия в сказочную страну или условной экскурсии в лес с элементами игры.

При обобщении темы “Нумерация чисел в пределах 20” можно предложить следующую ситуацию. Класс отправляется на луг ловить бабочек. Начинается игра “Поймай бабочку”:

Дидактическая цель: обобщение знаний о разрядном составе числа.

Содержание игры: на доску вывешивается иллюстрация с изображением луга и макеты бабочек. На каждой бабочке написан разрядный состав чисел до 20. У каждого ребёнка бабочка из картона жёлтого цвета, на обратной стороне которой записаны числа. Один из вызванных к доске учеников ловит бабочку, прикреплённую на ниточке, на которой указан разрядный состав числа, остальные ученики поднимают (ловят) тех бабочек, на которых написаны числа, соответствующие разрядному составу.

Потом все отправляются в магазин, (проголодались на прогулке). Далее проходит игра в “Магазин”:

Дидактическая цель: обобщение знаний учащихся о составе числа.

Содержание игры: вывешивается два плаката: один с рисунками монет, другой с изображением предмета и его ценой (хлеб – цена, батон, булочка, рогалик и т.п.). Дети подходят к плакатам, показывают хлеб, и расплачиваются за покупку набором из существующих монет.

Также при обобщении знаний по теме “Нумерация чисел в пределах 100” можно использовать следующие игры:

“Войди в ворота”

Дидактическая цель: обобщение знаний о составе числа.

Содержание игры: дети берут карточки с числами 0, 1, 2, … , 10. Два ученика образуют ворота (оба поднимают вверх сцепленные руки), в свободных руках они держат карточки с цифрами. В результате образуется несколько пар детей и один лишний. Он входит в ворота, выбирает ученика с такой карточкой, чтобы их числа в сумме составили число 10. Оба ученика проходят назад. Оставшийся без пары ученик также входит в ворота и подбирает пару себе. Все дети сидевшие за столами, следят за правильностью подбора пар.

Учитель школы №147 г.Санкт-Петербурга Е.А.Бочек на уроке обобщения знаний использовала игру-соревнование “Если вместе, если дружно” в 1 классе.[16] Особенность этой игры – эстафетный характер заданий, когда от вклада каждого, от чёткости и взаимодействия зависит общий результат.

Дидактическая цель: развитие логического мышления и воображения, проверка элементарных математических навыков.

Ход игры: учитель объявляет, что урок пройдёт в виде игры под девизом “Если вместе, если дружно”. Класс делится на две команды. Обе команды носят имена великих математиков прошлого: “Пифагоры”, “Архимеды” (желательны эмблемы). Учитель предупреждает, что соревнования будут эстафетными, поэтому будьте готовы проявить взаимопонимание и взаимовыручку.

 

 

 

Эстафета №1 “Очень длинный пример”

 

На доске написаны примеры. Каждый ученик из команды подбегает к доске по очереди, решает один пример и передаёт эстафету следующему. Кто быстрее и правильнее решит весь пример?

Эстафета №2 “Собери робота”

 

Участники команд берут из корзин геометрические фигуры (круги, треугольники, квадраты и т.п.) и крепят их на доске так, чтобы получилась фигура, напоминающая робота. У кого робот получится лучше?

Эстафета №3 “Каждому по примеру”

 

Количество примеров на доске соответствует числу участников команды. Участники команд по очереди подбегают к доске и решают по одному примеру (на выбор). Побеждает команда, которая быстро и без ошибок решит все примеры.

Эстафета №4: “Найди цифру”

 

На доске два плаката, где в беспорядке прикреплены цифры от 1 до 30. Участники команд по очереди снимают цифры по порядку и составляют числовой ряд. Побеждает команда, первая и правильно построившая полный числовой ряд.

 

 

 

 

 

 

Эстафета №5: “Без права на ошибку”

 

Команда выстраивается в шеренгу, у каждого в руках листок и карандаш. Ведущий читает задачу:

1. На одной жужаре к нам приехали 15 мямзиков, а на другой – на 7 мямзиков меньше. Сколько мямзиков приехало к нам на второй жужаре?

2. Когда Слюник видит, что кто-то нашёл пусик, он сразу начинает умирать от зависти. В четверг Мряка в присутствии Слюника нашла сначала 6 пусиков, а потом ещё 12 пусиков. Сколько раз Слюник умирал от зависти?

Каждый участник пишет ответ на листочке и показывает жюри, которое отмечает количество правильных ответов и неправильных. Ответ, не показанный до сигнала ведущего, не засчитывается.

Затем выстраивается другая команда и решает следующие задачи:

3. У Кости было 20 больших хрямзиков и 7 маленьких. Когда он узнал, что это такое, он всё побросал и отскочил подальше. Сколько хрямзиков бросил Костя?

4. Волк съел на своём Дне рождения трёх поросят, семерых козлят и одну Красную шапочку. Сколько сказочных героев съел Волк?

Побеждает команда, давшая большее количество верных ответов.

 

 

 

 

 

 

Эстафета №6: “Математическая сказка”

 

Все участники команды, говоря по одному предложению, продолжают сказку, которую начинает ведущий: первая команда “Однажды в математическом королевстве случилась беда…”, вторая команда “У Пятёрки был День рождения, и она пригласила на него своих друзей…”

После подводятся итоги урока. Какая команда была самая дружная, кому удалось лучше всех справится с трудными математическими заданиями? Награждение. Очень важно, чтобы ученики поняли в процессе игры: если вместе взяться за дело, то даже самые трудные примеры можно решить.

Если такая игра проводится в классе впервые, то учителю надо заранее позаботиться о помощниках (старшеклассниках, родителях), которые при необходимости помогли бы погасить возможные конфликты.

При подведении итогов важно отметить, сколь важны факты оказания помощи, проявления дружбы.

Состав команд в играх-соревнованиях в 1 классе должен меняться в каждой игре, чтобы у участников не появился конкретный постоянный соперник.

Важный педагогический момент игры – помочь учащимся осознать, что учиться вместе легче, чем поодиночке, что у них прекрасные одноклассники, которые всегда помогут.

Также при обобщении знаний детей довольно эффективно проходят игры “Освободи птичку” и “Незадачливый математик”.

 

 

 

“Освободи птичку”

Дидактическая цель: обобщение знания чисел от 21 до 100.

Содержание игры: птички находятся в клетке и учитель предлагает детям выпустить их на волю. Но для этого нужно выполнить задание. Учащиеся берут птичку из клетки и с обратной сторону читают задание (например, посчитай десятками до 60, назови число, в котором 2 дес. и 6 ед, и т.п.). Если ученик правильно ответит на вопрос, то птичка летит (переставляется) на дерево, если нет, то возвращается обратно в клетку.

“Незадачливый математик”

Дидактическая цель: обобщение знаний учащихся о замене числа суммой его разрядных слагаемых.

Средства обучения: кленовые листья, вырезанные из бумаги, с записанными на них числами и знаками, фигура Медвежонка.

Содержание игры: на доске записаны примеры с пропущенными числами и знаками.

43 = ÿ + 3	ÿ = 20 + 9	57 = 50 + ÿ
35 = 30 ÿ 5	1ÿ = 10 + 5	ÿ4 = 40 + ÿ

Немного в стороне крепятся вырезанные из бумаги кленовые листья с записанными на них цифрами и знаками и иллюстрация Медвежонка.

Учитель предлагает следующую ситуацию: “Ребята, Медвежонок решил примеры на кленовых листочках. Подул ветер и листочки разлетелись. Очень расстроился Медвежонок. Как же теперь быть? Надо помочь ему.” Ребята по очереди выходят к доске, ищут листочки с правильными ответами и заполняют ими пропуски. Данные игры помогают понять, насколько хорошо учащиеся усвоили пройденный материал.

Заключение

В процессе работы над темой на основе рассмотренной нами психолого-педагогической и методической литературы по данному вопросу, а также в результате исследования, мы пришли к выводу, что в педагогической работе большое внимание уделяется дидактической игре на уроке и выявлено её существенное значение для получения, усвоения и закрепления новых знаний у учащихся начальных классов.

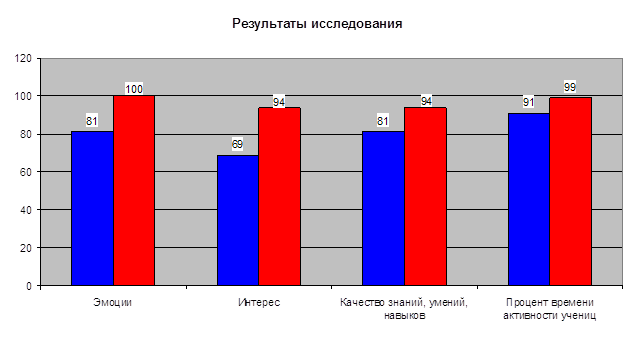
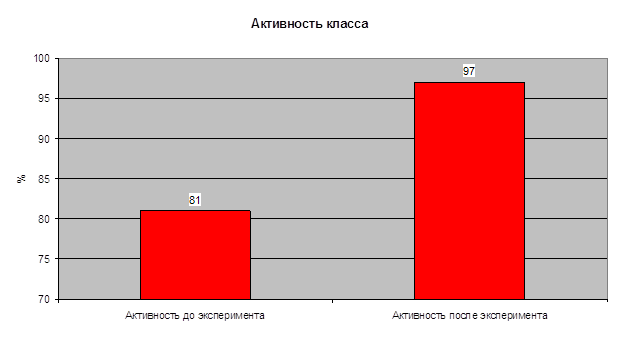
Проведя и проанализировав наши исследования, мы выявили, что дидактическая игра позволяет не только активно включить учащихся в учебную деятельность, но и активизировать познавательную деятельность детей. Игра помогает учителю донести до учащихся трудный материал в доступной форме. Отсюда можно сделать вывод о том, что использование игры необходимо при обучении детей младшего школьного возраста на данном конкретном уроке.

В ходе проделанной нами работы, мы сделали вывод, что дидактическая игра может быть использована как и на этапах повторения и закрепления, так и на этапах изучения нового материала. Она должна в полной мере решать как образовательные задачи урока, так и задачи активизации познавательной деятельности, и быть основной ступенью в развитии познавательных интересов учащихся.

Дидактические игры особенно необходимы в обучении и воспитании детей младшего школьного возраста. Благодаря играм удаётся сконцентрировать внимание и привлечь интерес даже у самых несобранных учеников. Вначале их увлекают только игровые действия, а затем и то, чему учит та или иная игра. Постепенно у детей пробуждается интерес и к самому предмету обучения.

Таким образом, дидактическая игра – это целенаправленная творческая деятельность, в процессе которой обучаемые глубже и ярче постигают явления окружающей действительности и познают мир.

Литература

1.  Аникеева Н.Б. Воспитание игрой. – М., 1987

2.  Амонашвили Ш.А. В школу – с шести лет. – М., 1986

3.  Бочек Е.А. Игра-соревнование “Если вместе, если дружно” //Начальная школа, 1999, №1.

4.  Выготский Л.С. Педагогическая психология. – М., 1991

5.  Жикалкина Т.К. Система игр на уроках математики в 1 и 2 классах. – М., 1996

6.  Карпова Е.В. Дидактические игры в начальный период обучения. – Ярославль, 1997

7.  Коваленко В.Г. Дидактические игры на уроках математики. – М., 1990

8.  Кружецкий В.А. Психология. – М., 1986

9.  Кушнерук Е.Н. Занимательность на уроках математики в начальных классах. – Минск, 1987

10.  Менджерицкая Д.В. Воспитателю о детской игре. – М., 1982

11.  Минскин В.И, От игры к знаниям. – М., 1988

12.  Перова М.Н. Дидактические игры и упражнения по математике. – М., 1996

13.  Попова В.И. Игра помогает учиться. //Начальная школа, 1987, №2.

14.  Перокова О.И., Сазанова Л.И. Раз, два, три – отвечай. – М., 1993

15.  Психолого-педагогические особенности проведения дидактических игр. Под.ред. Акшиной А., Акшиной Т., Жарковой Т. – М., 1990

16.  Сухомлинский В.А. О воспитании. – М., 1985

17.  Чилинрова Л.А., Спиридонова Б.В. Играя, учимся математике. – М., 1993

18.  Щедровицкий Г.П. Методические замечания к педагогическим исследованиям игры. // Психология и педагогика игры дошкольников. Под.ред.Запорожца – М.,1996

19.  Эльконин Д.Б. Психология игры – М., 1978

20.  Новосёлова С.Л. Игра дошкольника. – М., 1989

Приложения

Приложение 1

Анкета №1

 

Проводится с целью выявления отношения учителя к игре

1. Какое место, по Вашему мнению, занимает игра в развитии личности ребёнка в современных условиях?

- главное,

- не самое главное,

- второстепенное,

- никакого места не занимает,

- не задумывалась над этим,

- не знаю.

2. Сколько времени Вы в своей педагогической деятельности отводите дидактическим играм в учебном процессе?

- очень много,

- не очень много,

- только на уроках математики,

 - сегодня это не нужно,

- не задумывалась над этим,

- не знаю.

3. Какие трудности в проведении дидактических игр Вам мешают больше всего?

- отсутствие необходимых условий,

- равнодушие детей,

- не задумывалась над этим,

- не знаю,

- нет.

Приложение 2

Анкета №2

 

Проводится с целью выявления отношения детей к игре на уроке

1. Какие уроки ты больше всего любишь?

- с использованием таблиц, схем, рисунков,

- главное, чтобы было интересно,

- с использованием игры,

- урок он и есть урок, хоть что, всё равно скучно,

- не люблю любые уроки,

- не знаю, мне всё равно.

2. Если бы ты был учителем, чего бы у тебя было больше на уроке?

- таблиц, схем, рисунков,

- разных игр,

- самостоятельных работ,

- работ с учебником,

- индивидуальной работы по карточкам.

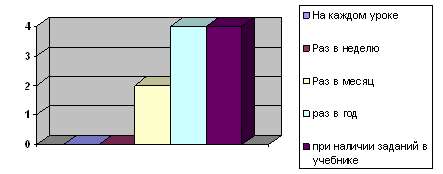
3. Как часто в вашем классе на уроках бывают игры?

- очень часто,

- часто,

- не очень часто,

- изредка,

- никогда.

4. Как ты относишься к игре на уроке?

- очень хочется участвовать,

- нет большого желания поддерживать игру,

- игра на уроке - пустая трата времени.

5. Как ты думаешь, какая польза от игры на уроке?

- очень большая,

- большая,

- не очень большая,

- небольшая,

- никакой пользы,

- не знаю.

Приложение 3

 

Конспекты уроков математики в 1 классе

Тема: “Числа от 21 до 100 (закрепление)”.

Цель: закрепить умение считать десятками, продолжить формирование понятия о поместном значении цифры, закрепить умение считать в пределах 100; развивать умение анализировать, грамотную математическую речь; поддерживать интерес детей к урокам математики.

Оборудование: карточки с числами (у каждого ученика), таблица чисел.

Содержание урока:

1. Оргмомент
2. Устный счёт	- Начнём урок с устного счёта. Первая наша игра “Найди лишнее число”. - Ребята, в каждом ряду из 5 последовательно записанных чисел - одно лишнее. Найдите это число и объясните, почему вы так решили. 5, 10, 15, 16, 20 (16 - лишнее) 8, 11, 13, 15, 17 (8) 10, 17, 16, 15, 14 (10) 12, 15, 18, 21, 43 (43) - Для следующего задания нам понадобятся ваши карточки с числами. Приготовьте их и поднимайте при ответе на вопрос. - увеличить10 на 3, уменьши 10 на 3; - найти сумму чисел 3 и 8; - найти разность чисел 8 и 3; - на сколько 8 меньше, чем 14; - на сколько 14 больше, чем 10. - Сравни числа: 41 и 14, 26 и 62, 43 и 43.
3. Игра	- Сейчас мы поиграем в интересную игру “Хлопки”. Мне понадобятся два помощника – один будет хлопать за десятки, а второй – за единицы в названном мною числе. Итак, будьте внимательны, а вы в классе тоже считайте внимательно. - А сейчас посчитаем в прямом и обратном порядке десятками от 10 до 100 по цепочке. - Молодцы, никто не сбился.
4. Постановка цели урока	- Сегодня мы продолжим изучать тему “Числа от 21 до 100”.  Посмотрите на наборное полотно. - Сколько выставлено квадратов?(23) Сколько десятков и единиц в этом числе? - Сколько выставлено кругов?(32) Сколько десятков и единиц в этом числе? - Давайте, сравним эту пару чисел 32 и 23. Чем они похожи? (одинаковые цифры) Что пишут на первом месте справа? на втором месте? Какой знак между ними поставили? - Ребята, сейчас я буду называть разрядный состав чисел, а вы в свои тетради запишите числа, соответствующие этим разрядам: 2 дес. 8 ед., 9 дес. 9 ед., 5 ед. 3 дес., 9 ед., 1 дес., 5 ед., 1 дес. 8 ед. - Итак, проверяем, какие числа вы записали: 28, 92, 99, 35, 19, 5, 18. - Посмотрите внимательно на числа и скажите, какое из них лишнее? (5) Почему? - Какие числа называются двузначными? однозначными? Подчеркните двумя чёрточками цифры, которые показывают число десятков в числах. Сколько десятков в каждом числе? - Подчеркните одной чертой цифры, которые обозначают число единиц.
5.Разбор задачи	- Чтение задачи с доски. Ребята заготовили для птиц 6кг рябины и 4кг семян арбуза. За зиму они скормили птицам 7 кг корма. Сколько килограммов корма осталось? - О чём говорится в задаче? Какие слова мы возьмём для краткой записи условия? - Что нужно найти? Можем ли мы найти сразу ответ? Что надо узнать сначала? - Как нам узнать, сколько заготовили семян? - Что надо для этого знать? - Во сколько действий будет задача? - Что мы найдём первым действием? вторым? - Записываем решение и ответ.
6. Игра	- А сейчас вы проверите друг друга, насколько хорошо вы умеете считать до 100 и поиграем в игру “Кто быстрей сосчитает?” - Посмотрите на доску. Там висит таблица, где записаны числа в неправильном порядке. Ваша задача – назвать все числа по порядку, так, как они следуют по порядку счёта от 61 до 90 и показать их на таблице.
		90	75	71	63	66
		67	82	86	68	78
		87	61	73	89	81
		74	88	65	77	84
		80	69	78	62	70
		64	83	72	79	85
	Через таблицу могут проходить и два игрока: Один называет числа от 61 до 74, другой – от 75 до 90. - А сейчас нужно назвать числа в обратном порядке от 90 до 61 и тоже показать их на таблице. Работа проходит в таком же порядке. Можно разделить отвечающих на 3 группы: 90-80, 79-69, 68-61).
7. Подведение итогов урока	- Молодцы, все справились с таким трудным заданием. - Итак, скажите, чем мы занимались сегодня на уроке? В какие игры мы играли? Что помогло повторить нам игры? - Урок окончен.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Сложение и вычитание двузначных чисел в пределах 100.

Цели: 1. Закрепить навыки сложения и вычитания двузначных чисел без перехода через десяток в пределах 100. 2. Развивать умение решать задачи изученных видов, навыки логического мышления. 3. Пробуждать интерес к предмету через дидактическую игру, логические задания.

Оборудование: рисунки с изображением Иван – Царевича, Змея Горыныча, Кощея; карточки с числами и буквами, орнамент из цифр для каллиграфической минутки, листки с примерами для групповой работы.

План:

1.  Оргмомент.

2.  Объявление темы урока.

3.  Каллиграфическая минутка.

 

Какая цифра спряталась в орнаменте?

Пропишем её¸. 2 2 2 2.

4.  Устный счёт.

В некотором царстве, в Тридевятом государстве жили-были Иван-Царевич и Василиса Прекрасная. Однажды Василиса исчезла. Иван-Царевич потужил, погоревал и отправился на поиски. Но куда идти, где искать? Кто похитил Василису? Мы узнаем выполнив первое задание.

1) Найдите “лишнее” число; расположите числа в порядке убывания. Теперь перевернём карточки. Что получилось? 35, 73, 33, 40, 13, 23.

73		35		33		23		13
К		О		Щ		Е		Й

Иван-Царевич отправился в путь. Но его уже поджидает Змей Горыныч, посланный Кощеем. Кто сразится со Змеем? Нужно победить все три головы Змея.

2) Индивидуальное задание у доски(3 человека).

38+2 65+5 28+2

46-4 87-3 39-6

46+40 87+10 39+30

82+8 56+6 76+4

100-20 50+30 90-40

75-5 91-90 83-3

59-30 36-2 49-3

59-3 36-20 49-30

Поведет Ивана-Царевича волшебный клубочек, но до него нужно добраться по лабиринту чисел (по возрастанию).

3) “Лабиринт”.

 

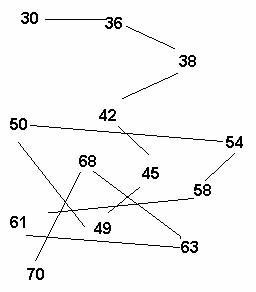
4) Волшебный клубочек привёл Ивана-Царевича на распутье. На придорожном камне надпись: “Верная дорога та, где ответ не самый большой и не самый маленький”. По какой дороге идти Ивану?

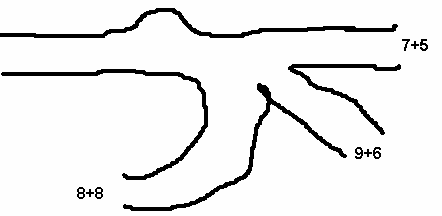
5)  а) А на дороге числа записаны рядами. Найдите закономерность, продолжите ряды чисел:

20, 17, 14, …, …, …, …

2, 4, 7, 11, …, …, …, …

б) Проверка индивидуального задания.

Ребята победили Змея Горыныча. Он охранял сундук, в котором находился меч для Ивана-Царевича. Но сундук крепко заперт тремя замками. А замки не простые - на каждом пример. Что скажете?

Замки откроются, если мы исправим ошибки, сделаем их невидимками. Стирать ничего нельзя, можно дописывать числа и знаки действия.

46=50 28+1=30 64>70

4+46=50 1+28+1=30 64>70-7 и др. числа до 70

46=50-4 28+1=30-1 любое число >6+64>70

Итак, меч в руках Ивана, путь в царство Кощея свободен!