Навигация
Задачи в школьном курсе математики
Лекционное занятие:
Задачи в школьном курсе математики
Содержание
1. Роль задач в обучении математике
2. Основные этапы в решении задачи. Общие умения по решению задач
3. Классификация задач. Роль алгоритмов и эвристик в обучении решению задач
4. Организация обучения решению математических задач
5. Системы упражнений и требования к ним
1. Роль задач в обучении математике
В психологии, дидактике известны попытки дать определение задачи. Например, одно из них: «Задача – объект мыслительной деятельности, содержащий требование некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи (отношения) между известными и неизвестными элементами» (Л.Л.Гурова. Психологический анализ задач. – Воронеж, 1976).
Задачи в обучении математике занимают важное место: это и цель, и средство обучения. Умение решать задачи – показатель обученности и развития учащихся.
При обучении математике задачи имеют образовательное, развивающее, воспитательное значение. Они развивают логическое и алгоритмическое мышление учащихся, вырабатывают практические навыки применения математики, формируют диалектико-материалистическое мировоззрение, являются основным средством развития пространственного воображения, а также эвристического и творческого начал.
При обучении теоретическим знаниям задачи способствуют мотивации введения понятий, выявлению их существенных свойств, усвоению математической символики и терминологии, раскрывают взаимосвязи одного понятия с другими.
В процессе изучения теоремы задачи выполняют следующие функции: способствуют мотивации ее введения; выявляют закономерности, отраженные в теореме; помогают усвоению содержания теоремы; обеспечивают восприятие идеи доказательства, раскрывают приемы доказательства; обучают применению теоремы; раскрывают взаимосвязи изучаемой теоремы с другими теоремами.
Воспитательное воздействие оказывает общий подход к решению задач: система задач, место, методы и формы ее решения, стиль общения учителя и учащихся, учащихся между собой при решении задач. Решение задач позволяет учащимся воспитывать в себе настойчивость, трудолюбие, активность, самостоятельность, формирует познавательный интерес, помогает вырабатывать и отстаивать свою точку зрения, воспитывать достоинство личности.
Развивающие функции задач заключаются в том, что в деятельности решения задач вырабатываются умения применять теоретические знания на практике, выделять общие способы решения, переносить их на новые задачи, развиваются логическое и творческое мышление, внимание, память, воображение.
С изменением роли и места задач в обучении обновляются и видоизменяются и сами задачи. Раньше они формулировались с помощью слов «найти», «построить», «вычислить», «доказать», в современной школе чаще используются слова «обосновать», «выбрать из различных способов решения наиболее рациональный», «исследовать», «спрогнозировать различные способы решения» и т д.
Решение задач является наиболее эффективной формой развития математической деятельности.
2. Основные этапы в решении задачи. Общие умения по решению задачПроцесс решения учебной задачи можно разделить на 4 основные этапы: осмысление условия задачи (анализ условия), поиск и составление плана решения, осуществление плана решения, изучение (исследование) найденного решения.
Осмысление условия задачи (1 этап).1). Умение анализировать требование задачи.
Под анализом требования задачи понимается выяснение возможных путей ответа на вопрос задачи. Одним из важнейших компонентов умения анализировать требование задачи является умение преобразовывать требование задачи в ему равносильное.
Например, докажем, что четырехугольник АВСD – квадрат, если докажем, что он поворотом на 90º отображается на себя.
Формирование этого умения связано с вооружением учащихся как можно большим числом признаков и свойств понятий;
2). Умение анализировать условие задачи.
Под анализом условия задачи можно понимать выявление такой информации, которая непосредственно не задана условием, но присуща ему.
Вся информация может быть разделена на три вида: а) информация, непосредственно заданная в условии; б) информация, полученная непосредственно из условия; в) информация, полученная уже из новой, т.е. выведенной ранее, информации.
Информация первого вида фиксируется чертежом и специальной записью под названием «дано».
Информация второго и третьего видов может быть получена следующими способами: а) получение следствий из непосредственно заданной информации; б) переосмысливания некоторых объектов (фигур, отношений между ними) в плане других понятий (например, АР – высота треугольника АВС. значит, АР![]() ВС; задан правильный треугольник, значит, можно найти радиус вписанной и радиус описанной окружности и т.п.); в) замена термина его определением; г) перечисление характеристических свойств понятий; д) интерпретация символических записей; е) перевод содержания задачи на язык специальной теории и наоборот (например, векторной) .
ВС; задан правильный треугольник, значит, можно найти радиус вписанной и радиус описанной окружности и т.п.); в) замена термина его определением; г) перечисление характеристических свойств понятий; д) интерпретация символических записей; е) перевод содержания задачи на язык специальной теории и наоборот (например, векторной) .
Часто внимание учащихся на информации второго и третьего вида не обращается, поэтому дальше выполнения рисунка и записей «дано» и «требуется доказать» самостоятельное решение не двигается.
Нужно учить школьников получать информацию второго и третьего вида. Полезны упражнения вида: 1) в треугольнике АВС двух сумма углов 90º. Что вы скажете о треугольнике АВС?; 2) АВСD – трапеция. Назовите несколько свойств этой фигуры; 3) Можно ли прямоугольник определить следующим образом: прямоугольником называется параллелограмм, имеющий прямую, содержащую середины его противоположных сторон, своей осью симметрии?; 4)![]() . Какой факт выражает эта запись?
. Какой факт выражает эта запись?
Очень важно на уроках выполнять анализ условия задачи всем классом.
Для того чтобы научиться решать задачи, надо приобрести опыт их решения. Редкие ученики самостоятельно приобретают такой опыт. Долг учителя - помочь учащимся приобрести опыт решения задач, научить их решать задачи. Однако помощь учителя не должна быть чрезмерной. Если учитель много будет помогать ученику, на долю последнего ничего не останется или останется слишком мало работы по приобретению опыта решения задач. Так ученик не научится решать задачи. Если же помощь учителя будет мала, ученик также может не научиться решать задача. Учитель должен помогать ученику путем советов, как решать задачу, или вопросов, отвечая на которые ученик успешнее решит задачу. Иногда учитель разыгрывает решение задачи, сам задавая вопросы и сам же отвечая на них. Ученики подражают ему в этом, постепенно приучаясь решать задачи. Но такой вариант обучения требует большей затраты времени и не всегда приводит к хорошим результатам. Можно сказать, что механическое подражание не метод обучения решению задач. Нужны вопросы и советы учителя ученику, вызывающие развивающие мыслительную деятельность школьников, помогающие развивать творческий подход к решению задач.
Такие вопросы и советы должны обладать общностью для различных задач, иначе ученики не научатся решать многие задачи, а будут учиться решать каждую конкретную задачу в отдельности. В то же время вопросы и советы должны быть естественны и просты, должны иметь своим источником простой здравый смысл. Они должны оказывать ученику действенную, но не назойливую помощь. Но одних вопросов и советов учителя ученику недостаточно для обучения решению задач. Нельзя забывать, что "умение решать задачи есть искусство, приобретаемое практикой" .
Вопросы и советы ученику условно можно подразделить на четыре группы. Это подразделение вопросов, вообще говоря, не является категоричным. Может оказаться, что вопросы, рекомендуемые для первого этапа, окажут помощь и на втором этапе, а рекомендуемые для второго этапа - на третьем и т. п. Дело в том, что этапы решения задачи не могут быть строго изолированы один от другого, между ними существует определенная связь, в их единстве заключается процесс решения задачи.
Вопросы и советы для осмысления условия задачи (1-й этап).
Нельзя приступать к решению задачи, не уяснив четко, в чем заключается задание, т. е. не установив, каковы данные и искомые или посылки и заключения.
Первый совет учителя: не спешить начинать решать задачу. Этот совет не означает, что задачу надо решать как можно медленней. Он означает, что решению задачи должна предшествовать подготовка, заключающаяся в следующем: а) сначала следует ознакомиться с задачей, внимательно прочитав ее содержание. При этом схватывается общая ситуация, описанная в задаче; б) ознакомившись с задачей, необходимо вникнуть в ее содержание. При этом нужно следовать такому совету: выделить в задаче данные и искомые, а в задаче на доказательство -посылки и заключения; в) если задача геометрическая или связана с геометрическими фигурами, полезно сделать чертеж к задаче и обозначить на чертеже данные и искомые (это тоже совет, которому должен следовать ученик); г) в том случае, когда данные (или искомые) в задаче не обозначены, надо ввести подходящие обозначения. При решении текстовых задач алгебры и начал анализа вводят обозначения искомых или других переменных, принятых за искомые; д) уже на первой стадии решения задачи, стадии понимания задания, полезно попытаться ответить на вопрос: "Возможно ли удовлетворить условию?" Не всегда сразу удается ответить на этот вопрос, но иногда это можно сделать.
Отвечая на вопрос: "Возможно ли удовлетворить условию?", полезно выяснить, однозначно ли сформулирована задача, не содержит ли она избыточных или противоречивых данных. Одновременно выясняется, достаточно ли данных для решения задачи.
Составление плана решения задачи (2-й этап). Составление плана решения задачи, пожалуй, является главным шагом на пути ее решения. Правильно составленный план решения задачи почти гарантирует правильное ее решение. Но составление плана может оказаться сложным и длительным процессом. Поэтому крайне необходимо предлагать ученику ненавязчивые вопросы, советы, помогающие ему лучше и быстрее составить план решения задачи, "открыть" идею ее решения:
1). Известна ли решающему какая-либо родственная задача? Аналогичная задача? Если такая или родственная задача известна, то составление плана решения задачи не будет затруднительным. Но далеко не всегда известна задача, родственная решаемой. В этом случае может помочь в составлении плана решения совет.
2). Подумайте, известна ли вам задача, к которой можно свести решаемую. Если такая задача известна решающему, то путь составления плана решения данной задачи очевиден: свести решаемую задачу к решенной ранее. Может оказаться, что родственная задача неизвестна решающему и он не может свести данную задачу к какой-либо известной. План же сразу составить не удается.
3). Стоит воспользоваться советом: "Попытайтесь сформулировать задачу иначе". Иными словами, попытайтесь перефразировать задачу, не меняя ее математического содержания.
При переформулировании задачи пользуются либо определениями данных в ней математических понятий (заменяют термины их определениями), либо их признаками (точнее сказать, достаточными условиями). Надо отметить, что способность учащегося переформулировать текст задачи является показателем понимания математического содержания задачи.
Некоторые авторы относят к переформулировке задачи и перевод ее на язык математики, т. е. язык алгебры, геометрии или анализа. Это, скорее, формализация задачи, "математизация" ее. К такому приему и приходится часто прибегать при решении многих текстовых задач.
4). Составляя план решения задачи, всегда следует задавать себе (или решающему задачу ученику) вопрос: "Все ли данные задачи использованы?" Выявление неучтенных данных задачи облегчает составление плана ее решения.
5). При составлении плана решения задачи иногда бывает полезно следовать совету: "Попытайтесь преобразовать искомые или данные". Часто преобразование искомых или данных способствует более быстрому составлению плана решения. При этом искомые преобразуют так, чтобы они приблизились к данным, а данные - так, чтобы они приблизились к искомым. Так, при каждом случае тождественных преобразований данные преобразуются, постепенно приближаясь к результату (искомому). Аналогично уравнение, систему уравнений, неравенство или систему неравенств преобразуют в равносильные, чтобы найти их корни или множество решений.
6). Нередко случается так, что, следуя указанным выше советам, решающий задачу все же не может составить план ее решения. Тогда может помочь еще один совет: "Попробуйте решить лишь часть задачи", т. е. попробуйте сначала удовлетворить лишь части условий, с тем чтобы далее искать способ удовлетворить оставшимся условиям задачи.
7). Нередко в составлении плана решения задачи помогает ответ на вопрос: "Для какого частного случая возможно достаточно быстро решить эту задачу?" Обнаружив такой частный случай, решающий ставит перед собой новую цель - воспользоваться решением задачи в найденном частном случае для более общего (но, может быть, не самого общего) случая. Так можно поступить, постепенно обобщая задачу до исходной, решаемой задачи. Предполагаемый вариант рассуждений - явное применение полной индукции. Итак, совет: "Рассмотрите частные случаи задачной ситуации, решите задачу для какого-нибудь частного случая, примените индуктивные рассуждения".
Осуществление плана решения задачи (3-й этап).
План указывает лишь общий контур решения задачи. При реализации плана решающий задачу рассматривает все детали, которые вписываются в этот контур. Эти детали надо рассматривать тщательно и терпеливо. Но при этом ученику (решающему задачу) полезно следовать некоторым советам:
1). Проверяйте каждый свой шаг, убеждайтесь, что он совершен правильно. Иными словами, нужно доказывать правильность каждого шага ссылками на соответствующие, известные ранее математические факты, предложения.
2). Обратить внимание учащихся на необходимость выбора такого способа оформления решения, чтобы зафиксировать решение в краткой и ясной форме.
Изучение найденного решения задачи (4-й этап).
Заключительный этап является необходимой и существенной частью решения задачи. Основным содержанием его должно быть осмысление выполненного решения, формулирование и решение (если это окажется возможным) других задач, явно связанных с решенной, и извлечение из всей проделанной работы выводов о том, как находятся и выполняются решения.
Таким образом, после оформления решения необходимо выявление идей (главной мысли), положенных в основу решения. Решение задачи несколькими способами является одним из путей проверки правильности полученного результата; важно сопоставление найденных решений, выделение более рациональных и поучительных. Это путь воспитания гибкости математического мышления и находчивости.
Даже очень хорошие ученики, получив ответ и тщательно изложив ход решения, считают задачу решенной. А ведь получение результата не означает еще, что задача решена правильно. Тем более не означает, что для решения выбран лучший, наиболее удачный, изящный, если можно так выразиться, вариант. По В. М. Брадису, задачу можно считать решенной, если найденное решение: 1) безошибочно, 2) обоснованно, 3) имеет исчерпывающий характер.
Итак, два совета: "Проверьте результат", "Проверьте ход решения". Проверка результата может производиться различными способами. Проверяя правильность хода решения, мы тем самым убеждаемся и в правильности результата. Значит, надо выполнить совет: "Проверьте все узловые пункты решения", еще раз убедитесь в истинности проведенных рассуждений.
Второй способ проверки результата заключается в получении того же результата применением другого метода решения задачи, поэтому полезно всегда задавать решающему вопрос: "Нельзя ли тот же результат получить иначе?" Иными словами, стоит последовать совету: "Решите задачу другим способом". Если при решении задачи другим способом получен тот же результат, что и в первом случае, задачу можно считать решенной правильно. К тому же получение различных вариантов решения одной и той же задачи имеет важное обучающее значение.
Изложенные выше советы для решения задач позволяют решать многие задачи, но, разумеется, не могут служить рецептом для решения любой задачи. Эти советы, многие из которых сформулировал Д. Пойа, правильно ориентируют решающего задачи на поиск решения, сокращают время решения многих задач, повышают вероятность отыскания верного и рационального способа решения задач. Единого же рецепта для решения любых задач попросту не существует.
От общих советов к частным. Начинать надо с общих вопросов, с общих советов, т. е. именно с тех, которые были приведены выше. Может оказаться, что общие вопросы не окажут помощи какому-то ученику. Тогда надо обратиться к дополнительным, более частным вопросам, так чтобы дойти до вопросов, соответствующих уровню развития и математической подготовке ученика. Переходить к частным, конкретным вопросам надо постепенно, чтобы на долю ученика досталась наибольшая часть работы по решению задачи. Задавая более частные, дополнительные вопросы, нужно учитывать следующее: вопросы должны быть такими, чтобы они направляли мысль ученика в нужную сторону, заставляя его активно мыслить над решением задачи. Разумеется, предлагая вопросы ученикам, надо предоставить время на обдумывание ответов на эти вопросы.
Общие умения по решению задачУмение самостоятельно решать задачи - важное умение не только для тех, кто будет в дальнейшей жизни заниматься математикой, но и для всех учащихся. Человеку в повседневной жизни приходится постоянно решать задачи и даже ставить их, правда, они несколько отличаются от школьных задач, иногда своей неопределенностью, иногда неразрешимостью. Умение организовать поиск - черта активной, самостоятельной личности. Умение самостоятельно решать задачи является показателем высокого интеллектуального развития. К сожалению, в школьной практике довольно часто можно наблюдать отсутствие этого умения. Из каких составляющих, из каких отдельных умений складывается общее умение решать задачи?
Это:
• умение проводить анализ условия задачи;
• умение применять изученную теорию (определение, теорему, правило) на практике; это умение предполагает узнавание возможности применения теории и собственно применение, поэтому теорема, определение, правило принимают в сознании вид алгоритма или предписания, по которому совершается действие;
• умение выделять основную идею в решении отдельной задачи, находить общее в решении нескольких задач и переносить эту идею, это общее на новую задачу;
• умения по самооценке своей деятельности, самоконтролю.
Как можно формировать умение анализировать условие задачи? Чтобы научиться анализировать условие задачи, анализ задачи должен стать целью обучения, что требует выполнения специальных заданий не по решению задач, а только по анализу их условия. По меньшей мере, этап анализа условия задачи должен быть специально выделен в процессе решения, и учащиеся должны иметь ориентировочную основу проведения этапа анализа. Анализу условия задачи следует обучать во всех разделах школьного курса математики: в арифметике, алгебре, геометрии. Как уже было отмечено, анализ условия задачи состоит в выделении данных и искомых, в выяснении значения каждого слова, в выяснении структуры задачи: какая и сколько ситуаций, объектов рассматриваются, какие величины входят в рассмотрение, каково соотношение между величинами в данной задаче, какая информация имеется в условии задачи в скрытом виде.
![]() Обучение краткой записи условия задачи - это и есть обучение анализу условия. Краткая запись- это модель текста задачи, материализованная форма проведения действия анализа условия. Этому следует обучать специально. Наиболее распространенной формой записи условия является запись отдельных ситуаций, например, следующим образом:
Обучение краткой записи условия задачи - это и есть обучение анализу условия. Краткая запись- это модель текста задачи, материализованная форма проведения действия анализа условия. Этому следует обучать специально. Наиболее распространенной формой записи условия является запись отдельных ситуаций, например, следующим образом:
I день - 273 стр.
П день - в 7 раз меньше
III день - на 45 стр. больше
а также в виде чертежей, диаграмм, рисунков (см. рис.).
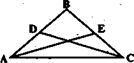
Рис. Краткая запись условия:
Дано: ![]() АВС, АВ = ВС, AD=DВ, BE = EC.
АВС, АВ = ВС, AD=DВ, BE = EC.
Доказать: АЕ=CD - это тоже материализованная форма анализа условия задачи, в которой понятия заменены их определениями.
При решении каждой задачи, способ решения которой неизвестен, используются синтетический и аналитический методы - происходит встречный процесс ot данных к требованию (синтез) и от требований к данным (анализ). На каком-то шаге устанавливается связь этих двух процессов - находится недостающий элемент, отношение - задача решена.
К какому бы разделу математики задача ни относилась, при ее решении происходит получение следствий из условия, какие-то условия заменяются эквивалентными, переформулируются, приобретают более удобный для операций вид, какие-то условия связываются. Установление связей между данными происходит не хаотично, а после выяснения отношений между данными под воздействием промежуточных и окончательных целей. Нахождение новых величин, отношений носит целенаправленный характер. Алгоритмов обучения творчеству нет, однако встречному движению от данных к требованию и от требования к условию можно обучать. Можно специально обучать получению следствий, переформулированию, решению задач с конца, другим эвристикам, демонстрируя их, акцентируя на них внимание, подбирая специальные задания.
Формированию умения анализировать условие задачи способствует выполнение обратных заданий: составить задачу по краткой схеме.
Начинать поиск решения задачи можно лишь тогда, когда ее условие полностью понято. Самоконтролем на этом этапе являются пересказ условия, подсчет данных и требования, проверка схем.
При осуществлении поиска основной идеи задачи продолжается выявление скрытых отношений, структуры задачи: рассматриваются под удобным углом зрения данные и требования, происходит сопоставление решаемой задачи с ранее решенными, конструируется модель задачи в соответствии с выдвигаемой гипотезой, осуществляется мысленный эксперимент, привлекаются различные эвристики.
В чем заключается деятельность по самоконтролю при анализе условия задачи? При анализе условия, как известно, осуществляется следующая деятельность: выделение данных и требований, выяснение смысла терминов; выделение объектов, ситуаций и величин, их характеризующих; моделирование ситуаций с помощью таблиц, чертежа, краткой записи условия задачи.
При этом самоконтроль осуществляется при пересказе текста задачи своими словами для выяснения, не забыто ли какое-либо данное, каждое ли слово в тексте понято. Если условие задачи моделируется с помощью чертежа, таблицы, то необходимо проверить, каждому ли данному нашлось место в этой модели. Для того чтобы проверить, правильно ли понято условие, можно рекомендовать восстановить текст задачи по краткой записи, модели, чертежу.
Вся эта деятельность направлена на то, чтобы выяснить, что задача понята целиком и правильно, структура задачи выделена и удерживается в памяти. Это обеспечивается обучением учащихся проводить анализ условий задачи.
При выдвижении гипотезы относительно возможного решения самоконтроль заключается в том, что решающему необходимо доказать себе, что выбор пути сделан правильно: что с помощью выбранной теоремы, правила, приема, определения можно довести решение задачи до логического конца; что задача подходит под определенный тип, предписание для которого имеется; что выбранная эвристика позволяет наметить ход решения задачи. Если ситуацию нельзя подвести под известный прием, если использованная эвристика заводит в тупик, если использованная теория не позволяет довести решение задачи до конца, необходимо отказаться от намеченного плана и продолжить анализ условия и привлечение новых идей.
Можно ли обучать учащихся самоконтролю на этом этапе?
Деятельности самоконтроля на этапе поиска плана решения задачи можно обучать, раскрывая эту деятельность, показывая, как учитель выходит из затруднительных ситуаций, которые возникают при поиске решения задачи. На этапе реализации полученного решения деятельность решающего состоит в применении выделенных эвристик, приемов, правил, определений, и при этом самоконтроль проявляет себя как пошаговый, пооперационный самоконтроль. Пошаговому контролю ученик обучается в рамках формирования различных приемов учебной работы и умственных действий, при обучении использованию определений, правил, теорем.
На ранее перечисленных этапах решения задачи самоконтроль проявляет себя как естественная неотрывная составляющая поисковой деятельности, которая может и не осознаваться решающим.
Последнему этапу решения задачи - проверке и исследованию полученного решения присвоен особый статус этапа, на котором осуществляется самоконтроль.
В методике преподавания математике выделены различные формы самоконтроля, проводимые после завершения этапа реализации намеченного плана. Приведем примеры таких форм.
1.Проверка с помощью частного случая. Например, если при решении неравенства получен некоторый числовой промежуток, то можно проверить некоторые конкретные значения переменной из этого промежутка.
2. Проверка совпадения размерности ответа с требованием задачи. Например, при нахождении пути значение скорости (км/ч) умножается на значение времени (ч). Умножение наименований должно дать наименование длины (км).
3. Проверка симметричности ответа, если в условии задачи какие-то данные симметричны. Например, если уравнения, входящие в систему, симметричны относительно переменных, то и найденные значения различных переменных должны быть равны.
4. Проверка ответа по здравому смыслу. Например, скорость пешехода не может быть равной 15 км/ч, количество рабочих не может быть дробным и т. д.
5. Проверка с помощью грубой прикидки. При этом данные грубо округляются и выясняется порядок возможного результата.
6. Проверка с помощью обратной задачи или с помощью другого способа решения.
7. Проверка текстовых задач, решенных с помощью составления уравнения, по смыслу. При этом необходимо, чтобы все промежуточные величины, зависящие от х, которые появляются в ходе решения задачи, имели бы смысл при полученном значении переменной.
Приведенные формы проверки, кроме 6, не дают полной гарантии правильно найденного и выполненного решения, но, тем не менее, с ними полезно ознакомить учащихся.
В работах, посвященных самоконтролю, предлагается следующая этапность в формировании самоконтроля: контроль за деятельностью учителя, взаимоконтроль - контроль учащихся за деятельностью товарища, контроль за собственной деятельностью. При этом речь, как правило, идет о контроле над исполнительской деятельностью. Такая последовательность имеет достаточное основание. Деятельность контроля состоит в сопоставлении, в сравнении двух действий: своего и контролируемого, а не просто в выполнении действия. Еще труднее посмотреть под новым углом зрения на свое исполнение действия.
Похожие работы
... в том, что с помощью с сюжетных задач обучаемый может познавать реальную действительность, осознавать те знания и умения, которые необходимы при решении любых задач, а не только сюжетных. 1.3 Методика обучения решению сюжетных задач в курсе математики 5-6 классов Сюжетной задачей называют такую задачу, в которой данные и связь между ними включены в фабулу. Содержание сюжетной задачи чаще ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
... угол 1800-α= по гипотенузе и острому углу: => OB1=OB; A1B1=AB => x = -x1,y = y1=> Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности. Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного ...
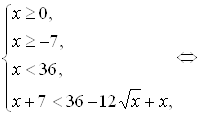
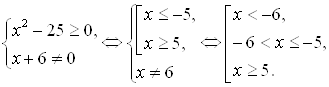
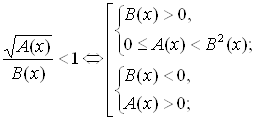
0 комментариев