Навигация
Классификация задач. Роль алгоритмов и эвристик в обучении решению задач
3. Классификация задач. Роль алгоритмов и эвристик в обучении решению задач
В современной методической и психологической литературе принята классификация задач. По характеру требования:
— задачи на доказательство;
— задачи на построение;
— задачи на вычисление.
По функциональному назначению:
— задачи с дидактическими функциями;
— задачи с познавательными функциями;
— задачи с развивающими функциями.
По величине проблемности:
— стандартные;
— обучающие;
— поисковые;
— проблемные.
По методам решения:
— задачи на геометрические преобразования;
— задачи на векторы и др.
По числу объектов в условии задачи и связей между ними:
— простые;
— сложные.
По компонентам учебной деятельности:
— организационно-действенные;
— стимулирующие;
— контрольно-оценочные.
Кроме того, различают задачи: стандартные и нестандартные; теоретические и практические; устные и письменные; одношаговые, двушаговые и др.; устные, полуустные, письменные и т.д.
При организации процесса обучения учащихся решению математических задач учитель сталкивается с вопросами: задачи какой сложности предложить ученикам, знакомы ли школьники с теми действиями, которые нужно применить при решении задач и т.п.
Если взять за основу следующую классификацию задач: на вычисление, на доказательство, на построение, на исследование, то такое деление не может быть инструментом в обучении школьников решению задач, потому что задачи этих видов не отличаются друг от друга уровнем сложности, характером деятельности человека по их решению. Например, в задачах на вычисление и построение приходится много доказывать, а в задачах на построение и доказательство приходится много исследовать и т.д., поэтому такая классификация задач ничего не дает. Кроме того, задачи делят на правильные, с противоречивыми данными, с лишними данными, теоретические и практические, стандартные и нестандартные и т.д.
В задаче выделяют основные компоненты:
1. Условие — начальное состояние;
2. Базис решения — теоретическое обоснование решения;
3. Решение — преобразование условия задачи для нахождения требуемого заключением искомого;
4. Заключение — конечное состояние.
Математическими считаются все задачи, в которых переход от начального состояния (1) к конечному (4) осуществляется математическими средствами, т.е. математическим характером компонентов: обоснование (2) и решение (3).
Если все компоненты задачи (условие, обоснование, решение, заключение) — математические объекты, то задача называется чисто математической, если математическими являются только компоненты решение и базис решения, то задача называется прикладной математической задачей.
На основе рассмотренной модели общего понятия задачи и ее основных компонентов строят дидактически направленную модель типологических особенностей задачи, зависящих от того, на каком этапе обучения эта задача предъявлена учащимся, какими знаниями и опытом обладают школьники в момент ее предъявления, в какой форме сформулирована задача и т.д.
Проблемный характер задачной системы определяется тем, какие из основных компонентов задачи неизвестны.
Стандартной называется задача, в которой четко определено условие, известны способ решения и его обоснование, а также даны упражнения на воспроизведение известного. Задача называется обучающей, если в ней неизвестен или плохо определен один из основных компонентов. Если неизвестны два компонента, задача назевается поисковой, а если три — проблемной.
Если рассматривать задачи как объект мыслительной деятельности учащихся, важно учитывать характер связей между элементами задачи, соотношение между воспроизводящей и творческой деятельностью учеников при решении задач, которое во многом определяется указанными связями.
Классификация задач, учитывающая характер связей между элементами задачи, соотношение между воспроизводящей и творческой деятельностью учеников:
— алгоритмические задачи;
— полуалгоритмические задачи;
— эвристические задачи.
Алгоритмические задачи — задачи, которые решаются с помощью непосредственного применения определения, теоремы, т.е. для решения которых имеется алгоритм. Например, задача на нахождение гипотенузы в прямоугольном треугольнике по известным катетам по формуле Пифагора. Применение алгоритма быстро и легко приводит к желаемому результату.
Полуалгоритмические задачи — задачи, правила решения которых носят обобщенный характер и не могут быть полностью сведены к объединению элементарных актов. Связи между элементами этих задач легко обнаруживаются учениками. Полуалгоритмические задачи в качестве подзадач содержат алгоритмические задачи. Например, известны две стороны треугольника и высота, опущенная на третью сторону. Необходимо найти периметр треугольника.
Решая полуалгоритмические задачи, ученик учится «сворачивать» знания, фиксируя их в сознании крупными блоками. При этом он начинает применять усвоенные алгоритмы в разных ситуациях.
Эвристические задачи — задачи, для решения которых необходимо выявить некоторые скрытые связи между элементами условия и требования или найти способ решения, причем этот способ не является очевидной конкретизацией некоторого обобщенного правила, известного ученику, или сделать и то и другое. Например, известны стороны треугольника. Нужно найти расстояние от середины высоты, проведенной к меньшей стороне, до большей стороны треугольника.
При решении эвристических задач ученик должен использовать эвристические приемы и методы.
Алгоритмические методы решения задач
Значительное количество задач предполагает при своем решений не творческую деятельность, а применение в основном определенного правила, формулы, определения, теоремы.
Например, для решения любого уравнения первой степени необходимо известные слагаемые перенести в правую часть, а слагаемые, содержащие неизвестные, перенести в левую часть, привести подобные члены и обе части уравнения разделить на коэффициент при неизвестном, если он отличен от нуля. Если он равен нулю, то поступают известным образом.
Приведенное правило - предписание алгоритмического типа, или алгоритм решения линейного уравнения. Правила сравнения чисел, действий над числами в различных числовых множествах, решения линейных, квадратных уравнений, неравенств - все это примеры алгоритмов. Под алгоритмом понимается точное общепонятное предписание о выполнении в определенной последовательности операций для решения любой из задач, принадлежащих некоторому классу.
Алгоритм может быть задан в виде таблицы, правила, формулы, определения, описания. Алгоритм может регламентировать действие с различной степенью подробности - свернутости, в зависимости от того, кому он предназначается. Если алгоритм предъявлен в форме последовательности команд, то это готовая программа действия. Приведем пример. Чтобы сложить десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы запятая была записана под запятой; 3) выполнить сложение, не обращая внимания на запятую; 4) поставить в ответе запятую под запятой в данных дробях (Випенкин Н.Я. и др. Математика 5- М., 2000).
Если алгоритм задан в виде формулы, правила, таблицы, определения, то программы нет. Ее предстоит создать решающему задачу. Рассмотрим в качестве примера определение решения системы неравенств с переменной как значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство. Определение подразумевает следующие шаги решения системы неравенств: 1) решить каждое неравенство; 2) найти пересечение полученных множеств.
Алгоритмы можно разделить на алгоритмы распознавания и преобразования. Признаки делимости, рассмотренные ранее алгоритмы подведения под определение и под понятие являются примерами алгоритмов распознавания. Алгоритмы по применению формул являются алгоритмом» преобразования. Однако при применении конкретной формулы, например, квадрата суммы двух чисел, вначале происходит узнавание формулы, доказательство того, что выбор формулы сделан правильно, а затем производится собственно преобразование: актуализация формулы и использование ее по шагам. Описанная деятельность состоит из следующих шагов: 1) найти первый член двучлена; 2) найти второй член двучлена; 3) возвысить первый член двучлена в квадрат; 4) составить произведение первого и второго членов двучлена; 5) удвоить результат предыдущего шага; 6) возвысить второй член двучлена в квадрат; 7) результаты третьего, пятого и шестого шагов сложить.
Значительное число различных правил в школьных учебниках математики в последнее время сообщается учащимся в форме алгоритма с выделенной последовательностью шагов. Использование правила в этом случае представляет собой меньшую трудность для учащихся, чем использование правила при отсутствии выделенных шагов или если какие-то операции - шаги действия в предписании пропущены, только подразумеваются и должны быть восполнены учащимися самостоятельно.
Рассмотрим правило сложения чисел с разными знаками в следующей форме: чтобы сложить два числа с разными знаками, надо: 1) из большего модуля вычесть меньший; 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
Этот алгоритм требует от школьника доработки, т. к. в нем не обозначены шаги: найти модуль каждого числа; сравнить модули и выделить число с большим модулем; определить знак числа, имеющего больший модуль. Эти шаги отдельными учащимися легко выполняются, а для других их выделение представляет существенные трудности.
В отдельных случаях операции, входящие в состав действий, приведены в учебниках в описательной форме или показаны на примерах, и для осуществления действий учащимся требуется выделить операции - отдельные шаги действия самостоятельно, как, например, при составлении пропорций при использовании подобия треугольников.
Проблема составления алгоритмов по изученному материалу связана с рядом важнейших проблем обучения математике: применение теоретических знаний на практике и развитие алгоритмического мышления. Под алгоритмическим мышлением понимается особый аспект культуры мышления, характеризующийся умением составлять и использовать различные алгоритмы.
Составлению, выделению алгоритмов необходимо специально обучать.
Это может происходить с помощью проведения обобщений при решении нескольких аналогичных задач. Необходимо обучать чтению формул словами, необходимо обучать переходу от речевой, формы в аналитическую и обратно, необходимо обучать строить программы действий в тех случаях, когда материал в книге или в рассказе предъявлен в описательной форме. Это и будет означать обучение применению теоретических знаний на практике и развитие алгоритмического мышления. Необходимо также обучать разворачивать, дополнять алгоритмы, предъявленные в готовой форме.
При использовании готовых алгоритмов целесообразно пользоваться компактным методом. Метод состоит в том, что (алгоритм) правило произносится по частям, на которые оно разбито по смыслу, и каждая операция выполняется вслед за произнесением соответствующего текста (пример приведите самостоятельно). Тем самым обеспечивается сознательное усвоение соответствующего правила. Компактный метод противопоставляется раздельному, когда произнесение правила целиком и его применение следуют друг за другом.
Вторая рекомендация по использованию алгоритмов вытекает из положений теории деятельности. Она заключается в требовании проведения всех операций, содержащихся в алгоритме (правиле) во внешнем плане и в развернутой форме, т. е. в написании и проговаривании всех операций без пропусков.
Типовые (полуалгоритмические) задачи и методы их решения
Рассмотрим две задачи, которые можно решить с помощью одной и той же теоретической базы - с помощью векторов.
ЗАДАЧА 1. Доказать, что диагонали ромба перпендикулярны.
Пусть ABCD - ромб. Для доказательства введем два неколлинеарных вектора: ВА и ВС и выразим векторы АС и ВD, расположенные на диагоналях, через введенные:
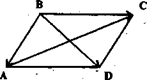
Чтобы доказать перпендикулярность векторов АС и BD, достаточно доказать равенство нулю их скалярного произведения.
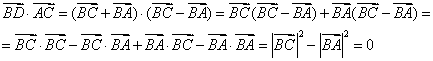
Равенство нулю скалярного произведения двух ненулевых векторов говорит о том, что косинус угла между ними равен 0°, а значит, угол между векторами - прямой, т. е. прямые, на которых располагаются рассматриваемые векторы, перпендикулярны.
ЗАДАЧА 2. Доказать с помощью векторов свойство средней линии трапеции.
Пусть АВСО - трапеция, точки Е и F-середины отрезка АВ и CD соответственно.
Введем векторы и выразим вектор EF из двух многоугольников:
![]() ;
; ![]() .
.
Сложим почленно полученные равенства:
![]() ,
,
![]() .
.
Последнее равенство можно интерпретировать следующим образом: т. к. векторы ВС и AD коллинеарны по определению трапеции, то и вектор EF также коллинеарен им, т. к. является линейной комбинацией этих векторов, а значит, отрезок EF параллелен основаниям трапеции. Т. к. векторы ВС и AD сонаправлены, то длина вектора ![]() равна сумме длин векторов ВС и AD и, следовательно, длина вектора EF равна полусумме длин векторов ВС я AD . А значит, длина отрезка EF соответственно равна полусумме длин отрезков ВС и AD .
равна сумме длин векторов ВС и AD и, следовательно, длина вектора EF равна полусумме длин векторов ВС я AD . А значит, длина отрезка EF соответственно равна полусумме длин отрезков ВС и AD .
Что можно заметить на примере решения приведенных двух задач? При их решении можно выделить одинаковую схему - одинаковые шаги решения, а именно:
введение удобным образом векторов;
переформулирование условия и требования задачи на язык векторов;
решение вновь сформулированной задачи с помощью векторного аппарата (определений, законов действий и т. д.);
интерпретирование результатов, полученных на языке векторов, на обычный геометрический язык.
По выделенной схеме решается как первая, так и вторая задача. По этой же схеме с помощью векторного аппарата можно решить многие геометрические задачи. Перечисленные шаги образуют прием решения задач векторным методом.
Этот прием учитель может представить ученикам в готовом виде. Но большую познавательную ценность имеет работа по самостоятельному выделению учащимися под руководством учителя шагов приведенного приема. Некоторые методисты отрицательно относятся к решению типовых задач как к натаскиванию. Однако учащиеся, знакомые с приемом, умеют решить не одну конкретную задачу, а целый класс задач, к которым они подходят с более высоких позиций обобщения учебного материала. Материал лучше структурируется, повышаются его уровень системности, возможности учащихся при решении задач. Ученик, не владеющий наиболее распространенными типами задач, не сможет решить ни одной нестандартной задачи или будет делать это со значительно большим усилием, чем тот, у кого в запасе владение многими типами задач.
Четыре выделенных шага образуют прием по решению задач данного типа. Этот прием можно отнести к полуалгоритмическим приемам, т. к. знание его не обязательно приведет решающего к получению верного результата, но может существенно облегчить поиск. Алгоритмические предписания являются той базой, владение которой облегчает решение задач.
В настоящее время учителями и методистами разработано много готовых приемов решения задач, но осталось место и для творчества.
Как организовать работу по выделению приема решения задач и его применению? Подготовка к приему может быть организована задолго до явного введения самого приема. Учащиеся решают задачи, а учитель старается акцентировать их внимание на средствах решения, на последовательности одних и тех же шагов. Этот период можно назвать пропедевтическим, подготовительным в формировании приема. Следующий этап - этап явного введения приема (предписания) с помощью учащихся на основе сравнения процессов решения выделенных задач. Далее организуется работа по закреплению шагов предписания и применению всего приема.
Самостоятельно составленное учителем предписание требует предварительной проверки на решении нескольких задач и внесения в него при необходимости корректировки.
В качестве еще одного примера приведем предписание по решению задач с помощью составления уравнений.
1. Определи, сколько и какие объекты, процессы, ситуации рассматриваются в задаче.
2. Укажи величины, которые характеризуют каждый объект, каждый процесс, ситуацию.
3. Установи зависимости, существующие между выделенными величинами.
4. Укажи, какие из выделенных величин известны.
5. Укажи неизвестные величины,
6. Определи зависимости между неизвестными величинами.
7. Выбери одно из неизвестных за x рациональным образом.
8. Вырази остальные неизвестные через х.
9. Выдели условие, оставшееся для составления уравнения.
10. Составь уравнение и реши его.
11. Сделай проверку и запиши ответ.
Рассмотрим применение предписания на конкретном примере.
ЗАДАЧА. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В, отстоящего от А на расстоянии 20 км, выехал мотоциклист. Скорость велосипедиста 12 км/ч, мотоциклиста 16 км/ч. На каком расстоянии от пункта А мотоциклист догонит велосипедиста?
Ответ на первый вопрос предписания предполагает появление двух строк таблицы:
| Участники |
| Велосипедист |
| Мотоциклист |
Ответ на второй вопрос предписания обосновывает появление трех столбцов таблицы:
| Участники | Скорость, км/ч | Время, ч | Расстояние, км |
| Велосипедист | |||
| Мотоциклист |
При ответе на третий вопрос ученики могут в устной форме указать зависимости между выделенными величинами. В отдельных случаях возможна их письменная запись. При ответе на четвертый вопрос в таблицу вносятся два числовых значения скорости - 12 и 16 км/ч. Ответ на пятый вопрос предполагает расстановку знаков вопроса в таблице вместо всех остальных величин. Ответ на шестой вопрос дополняет таблицу двумя отношениями:
| Участники | Скорость, км/ч | Время, ч | Расстояние, км |
| Велосипедист | 12 | ? | ? на 20 меньше |
| Мотоциклист | 16 | ? |
|
Шестым шагом предписания заканчивается анализ условия задачи, заполнив таблицу, учащийся воспринял структуру задачи и выделил ее условия.
Ответы на вопросы 7-9 помогают ученику в построении второй таблицы, которая приводит его к составлению уравнения:
| Участники. | Скорость, км/ч | Время, ч | Расстояние, км |
| Велосипедист | 12 | X |
|
| Мотоциклист | 16 | X |
|
Без пропедевтики приведенного приема, без специального обучения учащихся выделению процессов, величин, их характеризующих, установлению взаимосвязей между ними, составлению и уравниванию выражений введение приема нецелесообразно.
В заключение можно добавить, что подготовка учащихся к введению приведенного предписания, само введение и обучение пользоваться им могут осуществляться учителем на любом подходящем материале.
Попытайтесь самостоятельно построить стратегию обучения учащихся этому приему на разных этапах его формирования: на подготовительном этапе, на этапе введения в явном виде и на этапе закрепления.
Обучение соответствующим приемам - наиболее эффективный путь обучения решению задач различных типов.
Эвристические методы решения задачЗадачи можно разделить на стандартные и нестандартные. Нестандартная задача – это задача, решение которой не является для решающего известной цепью известных действий. Для ее решения учащийся сам должен изобрести (составить, придумать) способ решения.
Как производится поиск решения новой, нестандартной задачи? Универсального ответа на этот вопрос нет. Однако в каждой задаче, как в клубке ниток, можно обнаружить ту ниточку, потянув за которую, можно распутать весь клубок. Такой ниточкой является основная идея решения, один из общих методов решения, которые принято называть эвристиками. Эвристиками называются и отдельные методы решения задач, и учение об общих методах поиска решения задач. Эвристический метод-прием решения задачи не является приемом в полном смысле этого слова - системой определенных операций. Это, как уже сказано, основная идея решения задачи. Знание эвристик не дает гарантии того, что будет решена любая задача. Эвристики лишь помогают квалифицированно делать попытки поиска решения. При решении некоторых задач может быть использовано несколько эвристик. Учителю необходимо знание эвристик для того, чтобы помочь учащимся обнаружить их в собственной (учащихся) деятельности, разобраться в сущности методов и научиться ими пользоваться. Приведем примеры наиболее часто используемых эвристик и соответственно задач, которые решаются с их помощью.
Наиболее часто используемой эвристикой является метод восходящего анализа - решение задачи с конца, от требования - к условию. Эта эвристика осознанно или неосознанно, в большей или в меньшей степени используется при решении любой задачи.
ЗАДАЧА. Доказать, что в прямоугольном треугольнике биссектриса угла делит пополам угол между медианой и высотой, проведенными к гипотенузе (см. рис.).
При использовании метода анализа постоянно отыскивается ответ на вопрос, что достаточно найти, доказать, чтобы ответить на вопрос. Чтобы доказать равенство углов ОВК и КВМ, достаточно доказать равенство углов АВМ и СВО. А так как углы МВА и ВАМ равны, то для доказательства равенства углов СВО и МВА достаточно доказать равенство углов СВО и CAB. А доказать равенство этих углов уже не составит труда.
Достаточно универсальной является и другая эвристика - переформулирование. Суть этого эвристического приема заключается в том, что условия или требования, а возможно, то и другое одновременно, заменяются на новые, эквивалентные имеющимся, но позволяющие упростить поиск решения. В простейших случаях переформулировка - это замена термина его содержанием. Рассмотрим на примере эту эвристику.
ЗАДАЧА. Доказать, что середины оснований трапеции, точка пересечения диагоналей и продолжений боковых сторон лежат на одной прямой.
Оказывается, что поиск решения задачи облегчается, если задачу сформулировать иначе: доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений боковых сторон, делит основания трапеции пополам. Задача при этом остается той же, но новая формулировка подсказывает определенный метод решения.
Иногда при поиске решения трудной задачи помогает аналогия с использованием методов решения уже решенной задачи. Например, предстоит решить следующую задачу.
ЗАДАЧА. Через некоторую точку, расположенную вне окружности, проведена к этой окружности секущая. Доказать, что произведение отрезков АВ и АС (см. рис.) есть величина постоянная для данной окружности и данной точки.
Если к этому моменту оказывается уже решенной задача: «Доказать, что произведение отрезков хорд, проходящих через данную точку внутри данной окружности, есть величина постоянная», то можно перенести метод ее решения на новую задачу. А именно, вначале целесообразно переформулировать требование: проведя через точку А еще одну секущую, докажем, что АС·АВ = AE·AD. Чтобы доказать это равенство, преобразуем его в пропорцию ![]() , которая наталкивает на поиск подобных треугольников с названными сторонами.
, которая наталкивает на поиск подобных треугольников с названными сторонами.
При решении ряда задач может помочь метод суперпозиции - решение задач в частных случаях. Причем рассматриваемые частные случаи должны полностью исчерпывать все возможные случаи. Например, требуется доказать неравенство: ![]() .
.
Найти общее решение данной задачи можно, но довольно трудно, а решить ее в трех случаях, когда а < 0, ![]() и а >1, не представляет труда. Например, если а<0, то выражение слева можно представить как
и а >1, не представляет труда. Например, если а<0, то выражение слева можно представить как ![]() , которое принимает лишь положительные значения. Если
, которое принимает лишь положительные значения. Если ![]() , то его же можно представить как
, то его же можно представить как ![]() , и тогда очевидно, что оно принимает положительные значения в рассматриваемом промежутке. Если а>1, то выражение можно представить как
, и тогда очевидно, что оно принимает положительные значения в рассматриваемом промежутке. Если а>1, то выражение можно представить как ![]() . Рассмотренные три случая полностью исчерпывают все возможные значения параметра а.
. Рассмотренные три случая полностью исчерпывают все возможные значения параметра а.
Метод суперпозиции не следует смешивать еще с одной эвристикой - рассмотрением частных случаев, которые не исчерпывают всех возможных случаев. Тогда вывод, полученный по индукции, требует доказательства.
Иногда для поиска идеи решения задачи полезно рассмотреть какой-нибудь крайний, предельный случай. Эта эвристика так и называется «предельный случай». Рассмотрим задачу: доказать, что сумма расстояний от любой точки внутри правильного тетраэдра до его граней есть величина постоянная.
Чтобы доказать требование, желательно предварительно выяснить, что это за величина. Для этого и используется предельный случай. Возьмем в качестве произвольной точки одну из вершин тетраэдра. Тогда легко обнаружить искомую величину. Сумма расстояний от любой точки внутри тетраэдра до всех его граней равна высоте тетраэдра. С помощью предельного случая производится уточнение требования, его переформулировка, а для поиска пути доказательства могут быть привлечены другие эвристики.
Довольно часто при поиске решения задач может помочь еще одна эвристика - прием обобщения, когда вместо имеющейся задачи решается другая, более общая по отношению к данной.
Например, требуется определить, какое число больше: 19971998 или 19981997.
Преобразование разности этих выражений к успеху не приводит. Но если выражения прологарифмировать: 1998 lg 1997 и 1997 lg 1998, то вместо исходных можно сравнивать выражения ![]() и
и ![]() , тогда оказывается, что сравнивать надо два значения функции
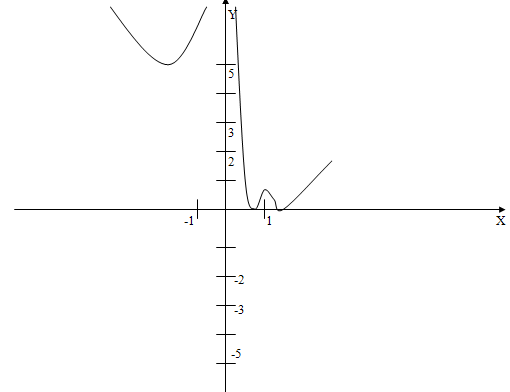
, тогда оказывается, что сравнивать надо два значения функции ![]() , т. е. требуется решить вопрос, какой характер монотонности имеет функция, а это стандартная задача.
, т. е. требуется решить вопрос, какой характер монотонности имеет функция, а это стандартная задача.
Очень важной эвристикой, используемой при решении большого числа задач, является выделение подзадач, решение которых не составляет труда, внутри основной задачи. Тем самым упрощается структура основной задачи.
ЗАДАЧА. Из двух пунктов, расстояние между которыми 100 км, выехали одновременно навстречу друг другу два велосипедиста. Скорость одного из них была 15 км/ч, а другого-10 км/ч. Вместе с первым велосипедистом выбежала собака со скоростью 20 км/ч. Встретив второго велосипедиста, собака повернула обратно и побежала навстречу первому велосипедисту. Встретив первого велосипедиста, она снова повернула. Собака бегала между велосипедистами до тех пор, пока велосипедисты встретились. Сколько километров пробежала собака?
Если решение задачи начинать с рассмотрения движения собаки и второго велосипедиста, то перед решающим встает необходимость рассматривать последовательность встречных движений, что может оказаться очень непростым делом. А если внутри основной задачи выделить в качестве элементарной подзадачи движение велосипедистов навстречу друг другу, в которой требуется определить время до их встречи, то сразу вырисовывается и вторая элементарная подзадача - движение собаки, скорость и время которой известны, а маршрут движения - безразличен.
Прием выделения подзадач внутри основной задачи применяется при решении подавляющего большинства задач. Этот прием используется, в частности, когда решается любая задача на описанные и вписанные в сферу многогранники, когда требуется, например, доказать, что центр сферы, вписанной в правильную пирамиду, лежит на высоте пирамиды; что основание перпендикуляра, опущенного из любой точки высоты пирамиды на боковую грань, попадает на апофему боковой грани. Не зная, как решить задачу, решающий часто проводит рассуждения по схеме: «По данным задачи я могу найти то-то и то-то, а что это мне дает для решения основной задачи?»
При решении ряда задач может оказаться полезным метод непрерывных величин. При этом используется следующее положение: если некоторая величина меняется непрерывно в зависимости от некоторой другой величины и при этом при разных значениях второй величины значения первой окажутся больше и меньше некоторого числа С, то это означает, что существует значение второй величины, при котором значение первой равно С. Рассмотрим задачу.
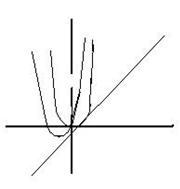
ЗАДАЧА. На плоскости начерчен квадрат и не перекрывающийся с ним треугольник (см. рис.). Существует ли прямая, которая разделила бы одновременно каждую из этих фигур на две равновеликие части.
Заметим, во-первых, что любая прямая, проходящая через центр квадрата, разбивает его на две равновеликие части. При этом справедливо и обратное предложение. Следовательно, задачу можно переформулировать следующим образом: провести через точку О прямую так, чтобы она разбивала треугольник на две равновеликие части. Вначале рассмотрим некоторую прямую l, не пересекающую треугольник.
Затем начнем вращать эту прямую вокруг точки О. Тогда оказывается, что при некотором положении прямой площадь «заметенной» части треугольника меньше ![]() , а в какой-то момент, при достаточном угле поворота прямой, эта прямая заметет площадь, большую
, а в какой-то момент, при достаточном угле поворота прямой, эта прямая заметет площадь, большую ![]() . Так как величина заметенной площади меняется непрерывно (малому изменению значения угла поворота соответствует малое изменение значения заметенной площади), то найдется такое значение угла поворота прямой, при котором величина «заметенной» части станет равной
. Так как величина заметенной площади меняется непрерывно (малому изменению значения угла поворота соответствует малое изменение значения заметенной площади), то найдется такое значение угла поворота прямой, при котором величина «заметенной» части станет равной ![]() .
.
Метод вспомогательных неизвестных - эвристика, используемая как при решении алгебраических задач, так и при решении геометрических задач. Рассматриваемый метод имеет три модификации: когда при замене число переменных или уменьшается, или увеличивается, или остается неизменным. Цепи введения вспомогательных неизвестных при этом различные. Рассмотрим три задачи.
ЗАДАЧА 1 . Доказать, что при любых действительных, отличных от нуля х и у, справедливо неравенство:
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
И вместо исходного неравенства получаем: ![]() или
или ![]() .
.
Неравенство (*) выполняется для всех U, кроме ![]() .
.
Однако ![]() , т.е.
, т.е. ![]() . Значит, исходное неравенство выполняется при всех допустимых значениях х и у.
. Значит, исходное неравенство выполняется при всех допустимых значениях х и у.
ЗАДАЧА 2. В качестве второго примера, когда при замене число переменных сохраняется, рассмотрим решение уравнения: ![]() .
.
Замена ![]() сводит исходное уравнение к достаточно хорошо известной форме:
сводит исходное уравнение к достаточно хорошо известной форме: ![]() .
.
В качестве третьего примера рассмотрим стереометрическую задачу.
ЗАДАЧА 3. Около правильной треугольной пирамиды с плоским углом ![]() при вершине описана сфера. Найти отношение объема пирамиды к объему шара, ограниченного сферой.
при вершине описана сфера. Найти отношение объема пирамиды к объему шара, ограниченного сферой.
В этой задаче требуется найти отношение величин. Объем выражается через значения каких-то линейных элементов, которые в задаче не заданы. Однако задача имеет решение, т. к. данный угол ![]() определяет всю задачную ситуацию с точностью до подобия.
определяет всю задачную ситуацию с точностью до подобия.
Оказывается, что если какой-нибудь линейный элемент, например, сторону основания пирамиды, взять за неизвестное х, то все остальные линейные величины можно выразить через х и![]() . При нахождении искомого отношения задачи вновь введенная переменная х сократится.
. При нахождении искомого отношения задачи вновь введенная переменная х сократится.
Ограничимся рассмотренными примерами эвристик как наиболее часто встречающихся при решении математических задач. Но не только математических. Методы анализа, переформулирования, рассмотрение частных и предельных случаев используются при решении физических, технических и задач других областей знаний.
Надо ли знакомить учащихся с эвристиками специально? Решающие находят, изобретают эвристики и сами. Но для этого нужны значительные усилия и время. Учителю полезно обратить внимание учащихся на метод, с помощью которого удалось осуществить поиск решения трудной задачи. Это можно сделать после решения задачи с помощью вопросов типа: «Как удалось переформулировать требование (условие) задачи?»; «Какие подзадачи удалось выделить, облегчив решение основной?»; «Как при решении задачи была использована аналогия?» Так постепенно вместе с учителем учащиеся осознают многие из используемых ими приемов, что позволит в дальнейшем сознательно привлекать их к решению других задач. При этом поиск решения становится более эффективным. Владение эвристиками расширяет творческие возможности учащихся.
И еще одно замечание относительно эвристик. Как правило, в чистом виде единичные эвристики при решений задач не применяются. Имеет место использование некоторой совокупности эвристик. Ни одна задача не обходится без методов анализа, переформулирования, выделения известных подзадач.
В методике Р.Г. Хазанкина, известного учителя из Белорецка, обучение эвристикам можно усмотреть в его методике решения «ключевых» задач. Ключевыми он называет задачи раздела, при решении которых раскрываются основные математические идеи, используемые для решения большого класса задач. Уроки решения «ключевых» задач проводятся в форме лекции, после чего учащиеся пытаются использовать рассмотренные идеи при решении других задач раздела.
Похожие работы
... в том, что с помощью с сюжетных задач обучаемый может познавать реальную действительность, осознавать те знания и умения, которые необходимы при решении любых задач, а не только сюжетных. 1.3 Методика обучения решению сюжетных задач в курсе математики 5-6 классов Сюжетной задачей называют такую задачу, в которой данные и связь между ними включены в фабулу. Содержание сюжетной задачи чаще ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...
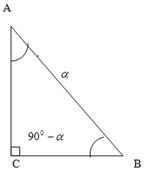
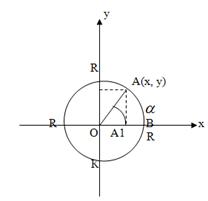
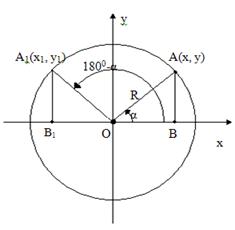
... угол 1800-α= по гипотенузе и острому углу: => OB1=OB; A1B1=AB => x = -x1,y = y1=> Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности. Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного ...
0 комментариев