Расчет и построение дифференциального и интегрального ТЗР

1.7.2 Расчет и построение дифференциального и интегрального ТЗР

Для нормального закона распределения

Так как при составлении статистического ряда (см. таблицу 4) были вычислены не статистические плотности функции распределения , а опытные вероятности попадания наблюдений в -й интервал , то для обеспечения сравнимости распределений вычислим теоретические вероятности этих же событий по зависимости:

, (11)

где  – длина интервала, принятая при построении статистического ряда;

 – квантиль нормального распределения, значение которого вычислено для середины -го интервала ;

 – значение центрированной и нормированной плотности распределения из приложения Г [1] (при этом следует учесть, что );

n - число интервалов, принятое при составлении статистического ряда.

Пример решения для середины 1-го интервала:

Значения теоретических вероятностей запишем в таблицу 6.

Таблица 6 - Значения теоретических вероятностей

Середина интервала, мм	0,025		0,031		0,038		0,044		0,050		0,057		0,063		0,070		0,076		0,082
Плотность функции распределения f(z)	0,11		0,19		0,29		0,37		0,4		0,37		0,29		0,19		0,11		0,05
Теоретическая вероятность		0,044		0,076		0,117		0,149		0,162		0,149		0,117		0,076		0,044		0,02

Вычисление функции распределения  осуществляется по зависимости:

; , (12)

где – квантиль нормального распределения, значение которого вычислено для конца -го интервала ;

 – значение интегральной функции нормального распределения (при этом следует учесть, что ).

Вычислим функцию распределения  на 1-м интервале:

.

Значения функции распределения запишем в таблицу 7.

Таблица 7 – Значения функции распределения

Границы интервала, мм	0,0220 ... 0,0284	0,0284 ... 0,0348	0,0348 ... 0,0412	0,0412 ... 0,0476	0,0476 ... 0,0540	0,0540 ... 0,0604	0,0604 ... 0,0668	0,0668 ... 0,0732	0,0732 ... 0,0796	0,0796 … 0,0860
Функция распределения	0,08	0,16	0,27	0,42	0,58	0,73	0,84	0,92	0,97	0,99

Используя значение функции распределения, можно определить теоретическое число интересующих нас событий (число отказов в i-м интервале) по формуле:

 (13)

Определяем теоретическое число отказов в 1-м интервале: отказов.

Определим значения теоретических чисел для каждого интервала и заполним таблицу 8.

Таблица 8 – Значения теоретических чисел для каждого интервала

Функция распределения	0,08	0,16	0,27	0,42	0,58	0,73	0,84	0,92	0,97	0,99
Теоретическая частота	8	8	11	15	16	15	11	8	5	2

Для закона распределения Вейбулла.

Рассуждая аналогично п. 1.7.2, вычислим не , а теоретические вероятности попадания СВ в -й интервал, например, вероятность отказа объекта в -м интервале по зависимости:

; , (14)

где a, b - параметры закона распределения, причем а параметр масштаба, имеющий размерность случайной величины t;

b - параметр формы (безразмерная величина);

 - смещение зоны рассеивания случайной величины t;

значения функции  приведены в таблице Е.2[1].

Параметр  определяют, используя коэффициент вариации. Из этого же приложения выбирают значения коэффициентов  и :

Параметр  рассчитывают по одному из уравнений:

 или .

 

Пример решения для середины 1-го интервала:

Значения теоретических вероятностей запишем в таблицу 9.

Таблица 9 – Значения теоретических вероятностей

Середина интервала, мм	0,025	0,031	0,038	0,044	0,050	0,057	0,063	0,070	0,076	0,082
Плотность функции распределения f(t)	0,2	0,55	0,78	0,84	0,84	0,74	0,57	0,48	0,32	0,19
Теоретическая вероятность	0,034	0,095	0,135	0,146	0,146	0,128	0,099	0,083	0,055	0,033

Функция распределения Вейбулла имеет вид:

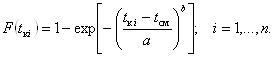 (15)

Данная функция зависит от двух аргументов – от параметра  и обобщенного параметра . Ее значения могут быть вычислены непосредственно по зависимости (15) или определены по таблице (приложение Ж [1]). Входами в эту таблицу являются:

– значение параметра ;

– значение обобщенного параметра ,

где  – значение случайной величины на конце i-го интервала.

Вычислим функцию распределения  на 1-м интервале:

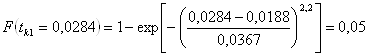
Значения функции распределения запишем в таблицу 10.

Таблица 10 – Значения функции распределения

Границы интервала, мм	0,0220 ... 0,0284	0,0284 ... 0,0348	0,0348 ... 0,0412	0,0412 ... 0,0476	0,0476 ... 0,0540	0,0540 ... 0,0604	0,0604 ... 0,0668	0,0668 ... 0,0732	0,0732 ... 0,0796	0,0796 … 0,0860
Функция распределения	0,050	0,148	0,286	0,443	0,598	0,732	0,835	0,907	0,951	0,977

Используя значение функции распределения, можно вычислить теоретическое число интересующих нас событий, например, число отказов машин в -м интервале по формуле:

 (16)

где N – общее число испытуемых (подконтрольных) объектов.

Определяем теоретическое число отказов в 1-м интервале:

Определим значения теоретических чисел для каждого интервала и заполним таблицу 11.

Таблица 11 – Значения теоретических чисел для каждого интпрвала

Функция распределения	0,050	0,148	0,286	0,443	0,598	0,732	0,835	0,907	0,951	0,977
Теоретическая частота	5	9,86	13,78	15,74	15,45	13,38	10,34	7,16	4,48	2,53

По вычисленным значениям  и  для всех интервалов строят графики  и , которые приведены в приложениях В и Г.

Результаты выравнивания опытных данных теоретическими законами распределения представим в виде таблицы 12.

Таблица 12 – Результаты выравнивания опытных данных теоретическими законами распределения

Границы интервала, мм			0,0220 ... 0,0284	0,0284 ... 0,0348	0,0348 ... 0,0412	0,0412 ... 0,0476	0,0476 ... 0,0540	0,0540 ... 0,0604	0,0604 ... 0,0668	0,0668 ... 0,0732
Середина интервала, мм			0,025	0,031	0,038	0,044	0,050	0,057	0,063	0,070
Опытная частота			5	11	17	14	15,5	7,5	8	12
Дифференциальный закон распределения	Опытная вероятность		0,05	0,11	0,17	0,14	0,155	0,075	0,08	0,12
	Теоретическая вероятность	НЗР	0,044	0,076	0,117	0,149	0,162	0,149	0,117	0,076
		ЗРВ	0,034	0,095	0,135	0,146	0,146	0,128	0,099	0,083
Интегральный закон распределения	Накопленная опытная вероятность		0,05	0,16	0,33	0,47	0,625	0,7	0,78	0,9
	Функция распределения	НЗР	0,08	0,16	0,27	0,42	0,58	0,73	0,84	0,92
		ЗРВ	0,050	0,148	0,286	0,443	0,598	0,732	0,835	0,907
Теоретическая частота		НЗР	8	8	11	15	16	15	11	8
		ЗРВ	5	9,86	13,78	15,74	15,45	13,38	10,34	7,16