Оцінювання випадкових похибок прямого вимірювання

1.2 Оцінювання випадкових похибок прямого вимірювання

Пряме вимірювання – це вимірювання однієї фізичної величини, значення якої знаходять безпосередньо: без перетворення її роду та використання функціональних залежностей.

Прямі багатократні вимірювання поділяються на рівно та нерівно точні. Рівно точними називаються вимірювання, що проводяться засобами вимірювання однакової точності за однією і тією ж методикою при незмінних зовнішніх умовах. При рівно точних вимірюваннях середні квадратичні відхилення результатів всіх рядів вимірювань рівні між собою.

Перед проведенням обробки результатів вимірювань необхідно переконатись в тому, що дані з вибірки, що оброблюються, статистично підконтрольні, групуються навколо одного й того ж центра і мають однакову дисперсію. Стійкість змін часто оцінюють інтуїтивно на основі тривалих спостережень. Однак існують математичні методи розв’язку поставленої задачі – методи перевірки однорідності. Щодо вимірювань, то розглядається однорідність груп спостережень, необхідні ознаки якої полягають в оцінці не зміщеності середніх арифметичних і дисперсій відносно один одного .

Задача обробки результатів багатократних вимірювань полягає в знаходженні оцінки вимірюваної величини і довірчого інтервалу, в якому знаходиться її дійсне значення.

Випадкові похибки рівно точних прямих вимірювань проявляються при багаторазових спостереженнях вимірюваної величини в однакових умовах одним оператором і за допомогою одного й того самого засобу вимірювання.

При статистичній обробці результатів багаторазових спостережень необхідно виконати наступну послідовність дій:

— провести багаторазові вимірювання і отримати масив Х1, Х2,…, Хn вимірювальної інформації;

— поправити результати вимірювання, вилучивши відомі систематичні похибки шляхом внесення поправок у результати спостережень;

— знайти математичне сподівання поправлених результатів спостереження і прийняти його за дійсне значення.

Для нормального закону розподілу, а якщо поступитися ефективністю оцінки, то й для всіх симетричних законів розподілу, за оцінку математичного очікування ряду рівноточних спостережень приймають середнє арифметичне, що визначається за формулою:

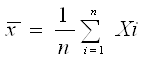;(1.3)

— визначити випадкове відхилення за наступною формулою:

; (1.4)

Дана різниця представляє собою випадкове відхилення (випадкову абсолютну похибку) при і-му спостереженні. Вона може бути позитивною та негативною.

Середнє арифметичне незалежно від закону розподілу має наступні властивості, що використовуються для перевірки правильності обчислення :

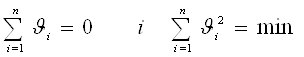;(1.5)

— обчислити середнє квадратичне відхилення результатів вимірювання за формулою Бесселя:

; (1.6)

Для серії n вимірювань однієї й тієї ж величини параметр S характеризує розсіювання результатів багаторазових n вимірювань однієї й тієї ж величини. Оскільки ми обчислюємо середнє арифметичне, необхідне для одержання оцінки S, то природно взяти його за результат вимірювання. Так як в даному випадку середнє арифметичне залежить від числа вимірювань і є випадковою величиною, та воно має деякі дисперсії відносно істинного значення;

— визначити квадратичне відхилення середнього арифметичного значення за формулою:

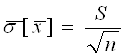 (1.7)

Отже, якщо в якості результату багаторазових вимірювань взяти середнє арифметичне , то випадкова похибка (S) зменшується в  раз порівняно з випадком, коли за результат вимірювання буде прийматися будь-яке одне з n спостережень. Тому багаторазові вимірювання з наступним усередненням результатів і прийняттям цього середнього за результат вимірювання є досить ефективним методом зменшенням випадкової похибки;

— визначити довірчі границі похибки вимірювання, що представляють собою верхню й нижню границі інтервалу, який накриває з заданою ймовірністю похибку вимірювання. Якщо число вимірювань n£30, то довірчий інтервал випадкової похибки при заданих ймовірності Р і середньому квадратичному відхиленню визначається за формулою Стьюдента:

, (1.8)

де kt – коефіцієнт Стьюдента, який залежить від заданої ймовірності Р і числа вимірювань n.

Щодо значення довірчої ймовірності, то в більшості випадків приймають Р=0.95. Якщо ж вимірювання повторити неможливо, то приймають Р=0.99, а в особливо відповідальних випадках, коли вимірювання, що виконуються, пов’язані з створенням нових еталонів або їхні результати можуть суттєво вплинути на здоров’я людини, приймають Р=0.997;

1.3 Оцінювання випадкових похибок опосередкованого вимірювання

Оцінку випадкових похибок опосередкованих вимірювань необхідно здійснювати за такою методикою:

1. Визначити для результатів прямих вимірювань  і  ;

2. Визначити значення невідомої величини

3. Визначити «вагу» кожної часткової похибки опосередкованих вимірювань

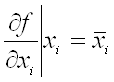. (1.9)

4. Обчислити часткові випадкові похибки опосередкованих вимірювань

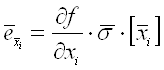. (1.10)

5. Знайти оцінку СКВ результату опосередкованих вимірювань

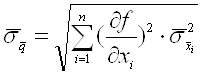,(1.11)

6. Знайти коефіцієнт kt Стьюдента за заданою довірчою ймовірністю Р і кількістю вимірювань n.

7. Знайти граничні значення випадкової складової похибки, яку приймають за похибку опосередкованого вимірювання

(1.12)

8. Записати результат опосередкованого вимірювання:

.(1.13)

Для визначення похибки результату опосередкованого вимірювання необхідно застосувати такі правила:

1. Якщо результат вимірювання представляється сумою або різницею двох і більше виміряних величин:

,(1.14)

і похибки Dх,..., Dw незалежні і випадкові, то абсолютна похибка результату може бути визначена за формулою

.(1.15)

Коли похибки аргументів корельовані, значення D може перевищувати отримане за попередньою формулою, але завжди буде задовольняти умову

.(1.16)

2. Якщо кінцевий результат вимірювання представляється добутком або часткою двох і більше виміряних значень:

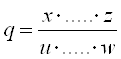 ,(1.17)

і похибки х,..., w незалежні і випадкові, то відносна похибка результату опосередкованого вимірювання визначається

. (1.19)

3. Якщо результат опосередкованого вимірювання є функцією однієї величини:

q = f(х), (1.20)

то похибка результату визначається

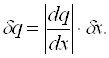(1.21)

4.  В загальному випадку похибка функції декількох величин

,(1.22)

похибки яких незалежні і випадкові, знаходиться

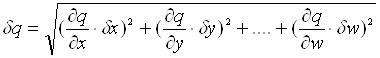,( 1.23)

але сумарна похибка ніколи не перевищить значення.

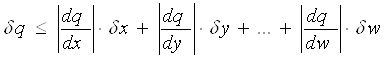.(1.24)

1.4 Оцінювання випадкових похибок сукупних та сумісних вимірювань

При сукупних та сумісних вимірюваннях невідомі величини хi , що підлягають безпосередньому вимірюванню, визначають за результатами вимірювання інших величин, які функціонально пов'язані з ними

φ(х1, х2, ... ,хn) =yj, (1.25)

де і=1, 2,....., n - порядковий номер невідомих величин х; j=1,2,...m - порядковий номер прямих вимірювань величин у.

Якщо результати прямих вимірювань Y містять випадкові похибки, то вони мають місце і в результатах сукупних (сумісних) вимірювань величин хi.

Розглянемо три випадки.

1.  Очевидно, що для m < n систему розв'язати неможливо.

2.  Для m=n розв'язання можливе, але похибки результатів вимірювання величин хi будуть, як і для прямих одноразових вимірювань, значними і числові значення цих похибок залишаються невідомими.

3.  Для m>n систему знову неможливо розв'язати алгебраїчно тому, що ці рівняння несумісні, оскільки праві частини рівнянь замість точних значень Yj містять результати їхніх вимірювань уj= Yj + ΔYj; із випадковими похибками ΔYj,.

Проте у останньому випадку для нормального закону розподілу похибок вимірювання величини уj можна знайти таку сукупність значень xі, яка з найбільшою ймовірністю задовольняла б початкові умови φ(х1, х2, ... ,хn) =yj. Це можна здійснити за допомогою методу найменших квадратів (принципу Лежандра).

Такий спосіб обробки експериментальних даних для сукупних (сумісних) вимірювань доцільно застосовувати для лінійних функцій. В інших випадках обробка результатів значно ускладнюється.

Тому розглянемо випадок, коли функції φj лінійні

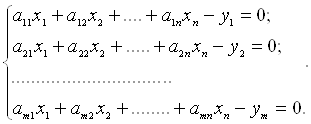 (1.26)

Цю ж систему представимо більш компактно

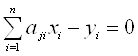, j=1,2,…m.(1.27)

Тут індекси при коефіцієнтах а показані у послідовності «рядок-стовпець».Ці рівняння називаються умовними. Через наявність похибок праві частини рівнянь дорівнюють не нулю, а деяким залишковим похибкам

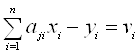, j=1,2,…m. (1.28)

Згідно з принципом Лежандра найбільш імовірними значеннями невідомих величин хі для цього випадку будуть такі, для яких сума квадратів залишкових похибок  мінімальна

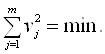(1.29)

Необхідною умовою такого мінімуму повинна бути рівність нулю похідних

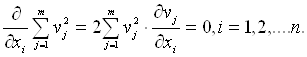(1.30)

Підставивши в формулу значення , отримують систему нормальних рівнянь

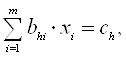
 ,(1.31)

яку в розгорнутому вигляді представляють так

(1.32)

Тут індекси при коефіцієнтах b показані у послідовності «рядок-стовпець» (h-і).

Оскільки кількість нормальних рівнянь завжди дорівнює кількості невідомих, то така система має розв'язок.

Загальний спосіб знаходження системи нормальних рівнянь полягає y знаходженні часткових похибок від кожної  по кожній з невідомих хi , перемноженням цих похідних на відповідні значення  та додаванні їх для кожної невідомої хі

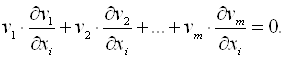(1.33)

Сукупність даних виразів представляє собою систему з n нормальних рівнянь.

Припустимо, що в результаті сукупних (сумісних) вимірювань отримай таку систему

(1.34)

Система нормальних рівнянь матиме вигляд

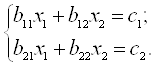(1.35)

Коефіцієнти  визначають із таких виразів

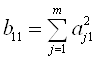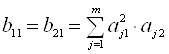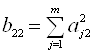; ; .(1.36)

Тоді значення  визначають

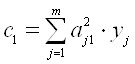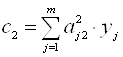; .(1.37)

Якщо кількість невідомих n< 4, то систему нормальних рівнянь доцільно розв'язувати за допомогою визначників. Розглянемо розв'язування систем нормальних рівнянь для n = 2 .

У цьому випадку складають та обчислюють головний визначник цієї системи рівнянь

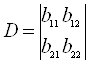.(1.38)

Далі складають та обчислюють часткові визначники  та D2, замінивши коефіцієнти  при відповідних невідомих на вільні члени  в системі рівнянь

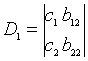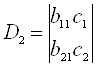; .(1.39)

потім знаходять найбільш імовірні значення невідомих

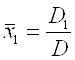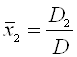; .(1.40)

Середні квадратичні значення результатів сукупних (сумісних) вимірювань. Після підстановки найбільш імовірних значень  до рівняння знаходять значення залишкових похибок  визначають  та суму квадратів залишкових похибок  .

Середнє квадратичне відхилення результатів сукупних (сумісних) вимірювань знаходять за формулою

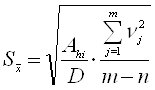,(1.41)

де m - кількість умовних рівнянь;

n - кількість невідомих;

 - ад'юнкти (алгебричні доповнення) елементів  головної діагоналі визначника D (для h=). які отримують викресленням h-го рядка та і-го стовпця, відповідне даному елементу , з наступним до множенням на

(-1)h+1. Для n=2 ад'юнкти: А11=b22; А22=b11.

Задавшись значенням довірчої ймовірності, знаходять відповідне значення коефіцієнта довіри tр. У цьому випадку число ступенів свободи дорівнюють:

.(1.42)

Довірчі границі випадкової похибки сукупних (сумісних) вимірювань становлять

. (1.43)

РОЗДІЛ 2 ОПРАЦЮВАННЯ РЕЗУЛЬТАТІВ ВИМІРЮВАННЯ