Навигация
Построение диаграммы изменения кинетической энергии и диаграммы "энергия-масса"
2.4.6 Построение диаграммы изменения кинетической энергии и диаграммы "энергия-масса"
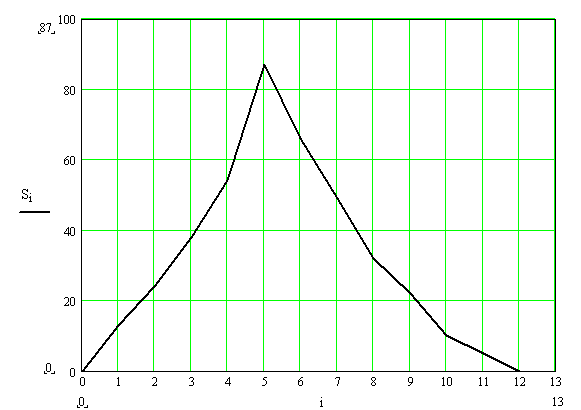
График изменения кинетической энергии ![]() построим путем вычитания ординат графика Ас(j) из соответствующих ординат графика Ад(j). После этого построим диаграмму Виттенбауера (неполная диаграмма"энергия-масса") путем графического исключения параметра j из графиков изменения кинетической энергии механизма и приведенного момента инерции.
построим путем вычитания ординат графика Ас(j) из соответствующих ординат графика Ад(j). После этого построим диаграмму Виттенбауера (неполная диаграмма"энергия-масса") путем графического исключения параметра j из графиков изменения кинетической энергии механизма и приведенного момента инерции.
2.4.7 Определение момента инерции маховика
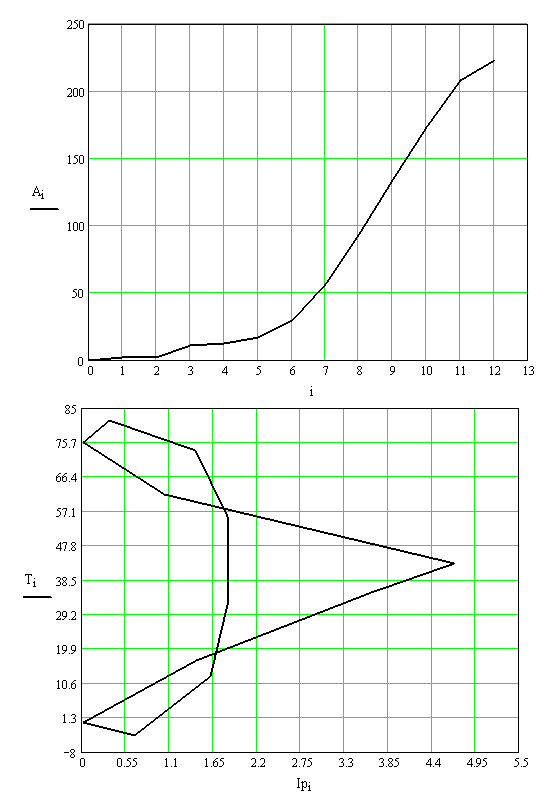
Для определения момента инерции маховика по заданному коэффициенту неравномерности движения следует провести касательные к графику "энергия-масса" под углами Ymax и Yminк оси абсцисс (оси приведенного момента инерции).
Тангенсы этих углов определим по формулам:
![]() , Ymax=88.45°
, Ymax=88.45°
![]() , Ymin=88.28°.
, Ymin=88.28°.
Диаметр маховика с тяжелым ободом: ![]() .
.
Для чугуна ![]() ;
;![]() ;
;![]() , отсюда:
, отсюда:
![]() ;
;
Mасса маховика: 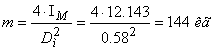 ;
;
Ширина обода: ![]() ;
;
Высота обода: ![]() .
.
2.4.8 Определение параметров маховика
Для построения графика w необходимо найти Iполн и Т по формулам:
![]() ;
;![]() .
.
![]() ;
;
![]() ;
;
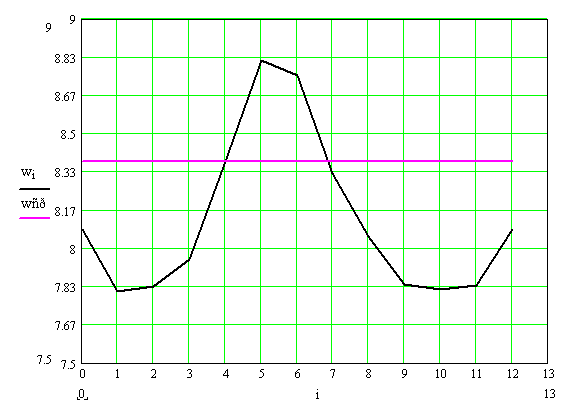
Имеем 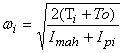 . Определяем угловую скорость для всех положений механизма. По расчетным данным определяем среднюю угловую скорость:
. Определяем угловую скорость для всех положений механизма. По расчетным данным определяем среднюю угловую скорость:
![]()
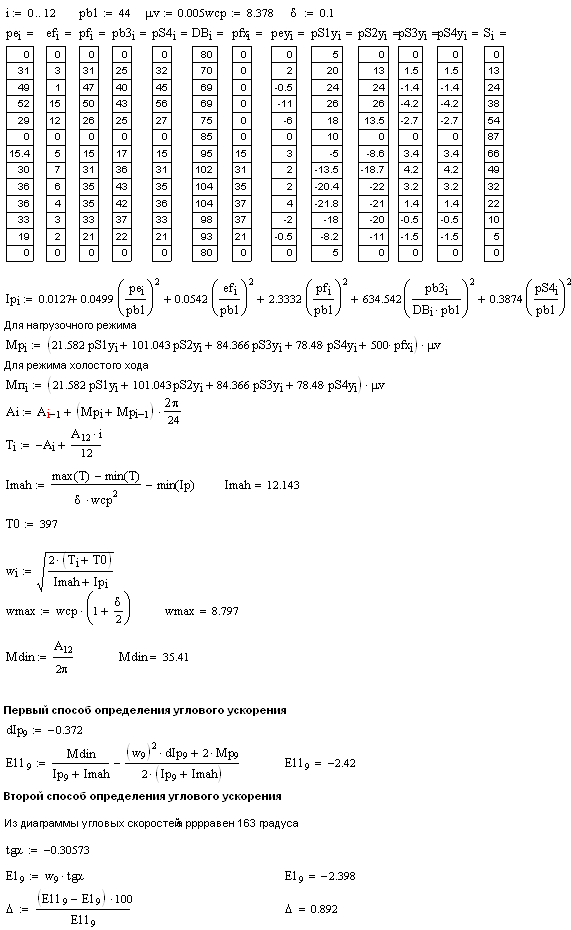
2.4.9 Расчет истинной угловой скорости звена приведения
Все расчёты и графики выполнены с использованием математического пакета MathCAD Professional 2001 и приведены ниже
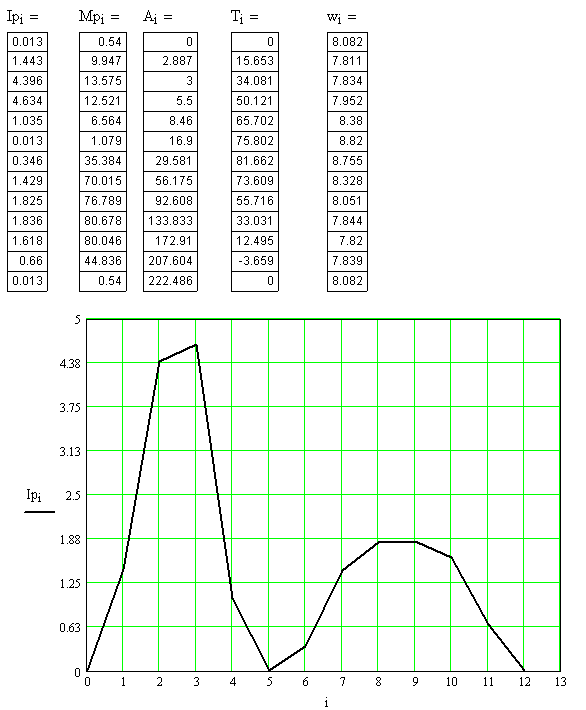

III Динамический анализ рычажного механизма
3.1 Определение линейных и угловых скоростей, ускорений точек и звеньев механизма
Для построения плана механизма в 9-ом положении примем масштабный коэффициент ![]() .
.
Для построения плана скоростей определим скорость точки В
![]()
Определим масштабный коэффициент
![]()
Построение плана ведется в соответствии с векторными уравнениями, рассмотренными в пункте II.
Переходим к построению плана ускорений. Так как кривошип вращается неравномерно, то ускорение точки В кривошипа равно:
![]() , где
, где
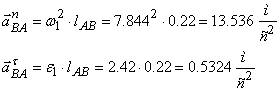
Выбрав масштабный коэффициент ![]() ,вычислим отрезки, изображающие aB1An и aB1At
,вычислим отрезки, изображающие aB1An и aB1At
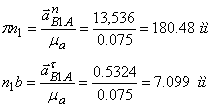
Из полюса p откладываем отрезок pn1||АВ, направленной к центру вращения, отрезок n1b^АВ откладываем в направлении e1.
Ускорение точки В3 найдем, решив графически систему векторных уравнений.
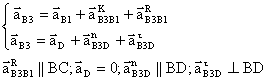 ;
;
Кариолисово ускорение определяем по формуле
![]()
На плане ускорений оно изображается отрезком
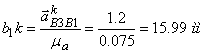
Вектор нормального ускорения ![]() равен:
равен:
![]()
![]()
На плане ускорений ![]() изображается отрезком
изображается отрезком
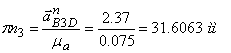 .
.
Ускорение точки С найдем по теореме подобия
![]()
Ускорение точек E и S3 найдем из соотношений
![]()
Для определения ускорения точки F составим два векторных уравнения.

В этих уравнениях aF0=0 и ![]() =0, так как направляющая XX неподвижна.
=0, так как направляющая XX неподвижна.

Действительные ускорения точек и звеньев равны:
![]()
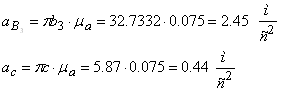
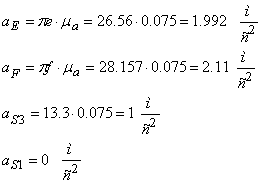
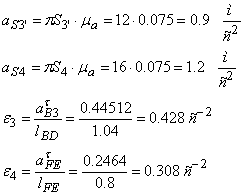
Похожие работы
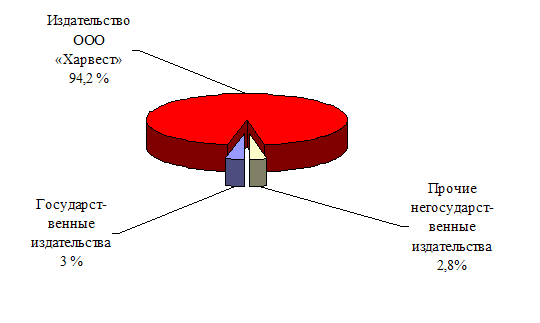
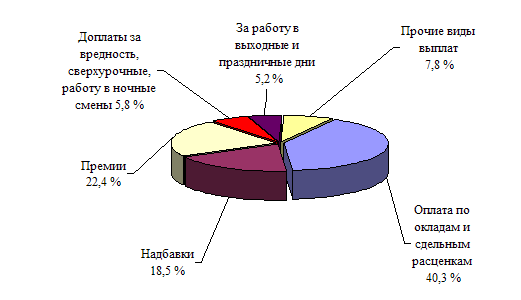
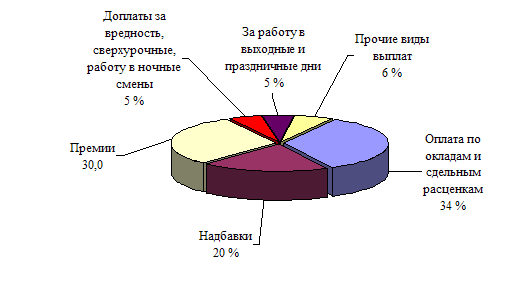
... . Дополнительным плюсом в данном направлении является то обстоятельство, что изменение условий премирования на предприятии позволит повысить уровень оплаты труда работников ОАО «Полиграфкомбинат «Красная Звезда»» без согласования в вышестоящей организации - Министерстве информации Республики Беларусь. Далее рассмотрим структуру фонда оплаты труда на предприятии (рис3.1.). Рис.3.1. Структура ...

0 комментариев