Метод сечений для определения внутренних усилий
Эпюры внутренних усилий при растяжении-сжатии и кручении
Понятие о напряжениях и деформациях
Свойства тензора напряжений. Главные напряжения
Упругость и пластичность. Закон Гука
Механические характеристики конструкционных материалов
Растяжение (сжатие) призматических стержней
Составные балки и перемещения при изгибе
Напряжения и деформации при кручении призматических стержней кругового поперечного сечения
Навигация
Метод сечений для определения внутренних усилий
Сопротивление материалов
85824
знака
1
таблица
44
изображения
2. Метод сечений для определения внутренних усилий
Ключевые слова: Внешние силы. Внутренние усилия (силовые факторы). Следящая система координат. Нормальная сила. Внутренние крутящие и изгибающие моменты. Поперечная сила.
Деформации рассматриваемого тела (элементов конструкции) возникают от прохождения внешней силы. При этом изменяются расстояния между частицами тела, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. При этом внутренние усилия определяются универсальным методом сечений (или метод Разреза).
Известно, что различают силы внешние и силы внутренние. Внешние усилия (нагрузки) - это количественная мера взаимодействия двух различных тел. К ним относятся и реакции в связях. Внутренние усилия - это количественная мера взаимодействия двух частей одного тела, расположенных по разные стороны сечения и вызванные действием внешних усилий. Внутренние усилия возникают непосредственно в деформируемом теле.
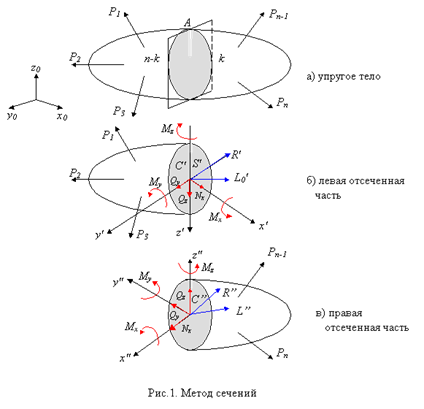
На рис.1 приведена расчетная схема бруса с произвольной комбинацией внешней нагрузки образующую равновесную систему сил:
(1)
При этом, реакции связей определяются из известных уравнений равновесия статики твердого тела:
, 
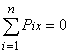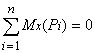(2)
, 
, 
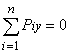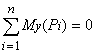
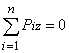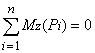
где х0, у0, z0 - базовая система координат осей.
Мысленное разрезание бруса на две части произвольным сечением А (рис.1 a), приводит к условиям равновесия каждой из двух отсеченных частей (рис.1 б,в). Здесь {S'} и {S"}- внутренние усилия, возникающих соответственно в левой и правой отсеченных частях вследствие действия внешних усилий.
При составлении мысленно отсеченных частей, условие равновесия тела обеспечивается соотношением:
Так как исходная система внешних сил (1) эквивалентна нулю, получаем:
{S'} = -{S"} (3)
Это условие соответствует четвертой аксиоме статики о равенстве сил действия и противодействия.
Используя общую методологию теоремы Пуансо о приведении произвольной системы сил к заданному центру и выбрав за полюс приведения центр масс, сечения А', точку С', систему внутренних усилий для левой части {S'} сводим к главному вектору 
и главному моменту 
внутренних усилий. Аналогично делается для правой отсеченной части, где положение центра масс сечения А" определяется, соответственно, точкой С" (Рис.1 б,в).
{S'} ~ {R',L'0}; {S"} ~ {R",L"0} (4)
Здесь в соответствие с четвертой аксиомой статики по-прежнему имеют место следующие соотношения:
R' = -R" (5)
L'0 = -L"0
Таким образом, главный вектор и главный момент системы внутренних усилий, возникающие в левой, условно отсеченной части бруса, равны по величине и противоположны по направлению главному вектору и главному моменту системы внутренних усилий, возникающих в правой условно отсеченной части.
График (эпюра) распределения численных значений главного вектора и главного момента вдоль продольной оси бруса и предопределяют, прежде всего, конкретные вопросы прочности, жесткости и надежности конструкций.
Определим механизм формирования компонент внутренних усилий, которые характеризуют простые виды сопротивлений: растяжение-сжатие, сдвиг, кручение и изгиб.
В центрах масс исследуемых сечений С' или С" зададимся соответственно левой (с', х', у', z') или правой (с", х", у", z") системами координатных осей (рис.1 в), которые в отличие от базовой системы координат x, у, z будем называть "следящими". Термин обусловлен их функциональным назначением. А именно: отслеживание изменения положения сечения А (рис.1 а) при условном смещении его вдоль продольной оси бруса, например при: 0 ≤ х'1 ≤ а, а ≤ x'2 ≤ b и т.д., где 0, а и b - линейные размеры границ исследуемых участков бруса.
Зададимся положительными направлениями проекций главного вектора или 
и главного момента или 
на координатные оси следящей системы (рис.1 б, в):
{N', Q'y, Q'z}, {M'x, M'y, M'z} (6)
{N", Q"y, Q"z}, {M"x, M"y, M"z}
При этом положительные направления проекций главного вектора и главного момента внутренних усилий на оси следящей системы координат соответствуют правилам статики в теоретической механике: для силы - вдоль положительного направления оси, для момента - против часовой стрелки при наблюдении со стороны конца оси. Они классифицируются следующим образом:
Nx - нормальная сила, признак центрального растяжения или сжатия;
Мx - внутренний крутящий момент, возникает при кручении;
Qz, Qу - поперечные или перерезывающие силы - признак сдвиговых деформаций,
Му, Мz - внутренние изгибающие моменты, соответствуют изгибу.
Соединение левой и правой мысленно отсеченных частей бруса приводит к известному (3) принципу равенства по модулю и противоположной направленности всех одноименных компонент внутренних усилий, а условие равновесии бруса определяется в виде:
{P1, P2, P3, ... , N', N", Q'y, Q"y, Q'z, Q"z, M'x, M"x,
M'y, M"y, M'z, M"z, ... , Pn-1, Pn} ~ 0 (7)
С учетом эквивалентности нулю исходной системы сил (1) имеет место:
{N', N", Q'y, Q"y, Q'z, Q"z, М'x, M"x, M'y, M"y, М'z, M"z}~0 (8)
Как естественное следствие из соотношений 3,4,5 полученное условие является необходимым для того, чтобы одноименные компоненты внутренних усилий попарно образовали подсистемы сил эквивалентные нулю:
{N', N"} ~ 0 > N' = -N"
{Q'y, Q"y} ~ 0 > Q'y = -Q"y
{Q'z, Q"z} ~ 0 > Q'z = -Q"z
{М'x, M"x} ~ 0 > М'x = -M"x
{M'y, M"y} ~ 0 > M'y = -M"y
{М'z, M"z} ~ 0 > М'z = -M"z (9)
Общее число внутренних усилий (шесть) в статически определимых задачах совпадает с количеством уравнений равновесия для пространственной системы сил и связано с числом возможных взаимных перемещений одной условно отсеченной части тела по отношению к другой. Эти перемещения могут наблюдаться при разрушении тела по этому сечению.
Искомые усилия определяются из соответствующих уравнений для любой из отсеченных частей в следящей системе координатных осей. Так, для любой отсеченной части соответствующие уравнения равновесия приобретают вид;
ix = N + P1x + P2x + ... + Pkx = 0 N
iy = Qy + P1y + P2y + … + Pky = 0 Qy
iz = Q + P1z + P2z + ... + Pkz = 0 Qz
x(Pi) = Mx + Mx(Pi) + ... + Mx(Pk) = 0 Mx
y(Pi) = My + My(Pi) + ... + My(Pk) = 0 My
z(Pi) = Mz + Mz(Pi) + ... + Mz(Pk) = 0 Mz (10)
Здесь для простоты обозначений системы координат с' х' у' z' и с" х" у" т" заменены единой оxуz.
Уважаемые коллеги! Таким образом, механизм предложенного автором лекций метода построения эпюр внутренних усилий, освобождающий Вас от механического запоминания "правил знаков" при построении эпюр внутренних усилий, заключается в следующем:
Определите реакции в связях по величине и направлению в базовой системе координат.
Определите количество участков бруса для использования метода сечений.
Мысленно рассеките брус в пределах исследуемого участка и изобразите на Ваше усмотрение левую или правую условно отсеченную часть.
Укажите пределы изменения положения сечения вдоль продольной оси в базовой системе координат на этом участке.
Введите в искомом сечении соответственно левую или правую следящую систему координатных осей.
Задайтесь положительными направлениями внутренних усилий в следящей системе координат.
Составьте уравнения равновесия для рассматриваемой условно отсеченной части бруса в следящей системе координат.
Определите из уравнений равновесия искомые внутренние усилия.
Вычислите искомые внутренние усилия на границах участков и при необходимости, - их экстремальные значения.
Выбрав масштаб усилий, выполните построение эпюры в соответствие с полученными их модульными значениями и знаками.
Указанная последовательность действий (кроме п.1) составляет суть метода сечений (разреза), единственного метода для определения внутренних усилий.
Не забываем, что при распределенной нагрузке в соответствие с теоремой Вариньона векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.
Эпюры внутренних усилий позволяет визуально найти положение опасного сечения, где действуют наибольшие по модулю внутренние усилия. В этом сечении при прочих равных условиях наиболее вероятно разрушение конструкции при предельных нагрузках.
Похожие работы
... мощности · Ваттметр · Варметр · Фазометр 2. Основные понятия: сопротивление материалов Сопротивление материалов, наука о прочности и деформируемости элементов (деталей) сооружений и машин. Основные объекты изучения Сопротивление материалов – стержни и пластины, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и ...
... шрифт Times 16пт; «Курский государственный технический университет» - шрифт №5; в компьютерном варианте шрифт Times 14пт; «Кафедра сопротивления материалов и строительной механики» - шрифт №5; в компьютерном варианте шрифт Times 14пт; названию расчетно-графической работы – шрифт №10; в компьютерном варианте Times 18пт; «расчетно-графическая работа №…» - шрифт №7; в компьютерном варианте Times ...
... сечение 1 мм2 Сопротивление проводника зависит не только от материала, из которого он изготовлен, оно зависит и от его размеров длины и поперечного сечения. где - удельное сопротивление l - длина S – площадь поперечного сечения Схема: Оборудование: приборный щит № 1 амперметр 0 – 1А Вольтметр 0 – 150 В Медный провод Æ ...
... . Электропроводность диэлектриков очень мала, так как переход заметного числа электронов в зону проводимости - случайное явление, обусловленное, например, дефектами структуры. Электрическое сопротивление - свойство материалов как проводников противодействовать электрическому току. Вес вещества, помещенные во внешнее магнитное поле, намагничиваются. Намагничивание связано с наличием магнитных ...
0 комментариев