Метод сечений для определения внутренних усилий
Эпюры внутренних усилий при растяжении-сжатии и кручении
Понятие о напряжениях и деформациях
Свойства тензора напряжений. Главные напряжения
Упругость и пластичность. Закон Гука
Механические характеристики конструкционных материалов
Растяжение (сжатие) призматических стержней
Составные балки и перемещения при изгибе
Напряжения и деформации при кручении призматических стержней кругового поперечного сечения
Навигация
Эпюры внутренних усилий при растяжении-сжатии и кручении
Сопротивление материалов
85824
знака
1
таблица
44
изображения
3. Эпюры внутренних усилий при растяжении-сжатии и кручении
Ключевые слова: Нормальное сечение. Нормальная сила. Внутренний крутящий момент.
Эпюры внутренних усилий при растяжении-сжатии
Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только нормальная сила.
Рассмотрим расчетную схему бруса постоянного поперечного сечения с заданной внешней сосредоточенной нагрузкой Р и распределенной q, (рис.1).
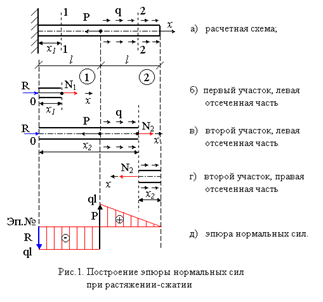
Пусть 
. Прежде всего определим опорную реакцию R, задавшись ее направлением вдоль оси х.
Брус имеет 2 участка 
и 
.
В пределах первого участка мысленно рассечем брус на 2 части нормальным сечением и рассмотрим равновесие, допустим левой части, введя следующую координату х1, рис.1 б:
Следовательно, в пределах первого участка брус претерпевает сжатие постоянной нормальной силой.
Аналогично поступим со вторым участком. Мысленно рассечем его сечением 2-2, и рассмотрим равновесие левой части (рис.1 в).Установим предварительно границы изменения х2:
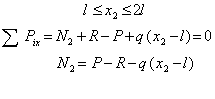
Подставляя граничные значения параметра х2, получим:
Таким образом, в пределах второго участка брус растянут и нормальная сила изменяется по линейному закону.
Аналогичный результат получается и при рассмотрении правой отсеченной части (рис.1 г):
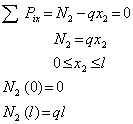
На основе полученных данных строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (рис.1 д). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил R и Р.
Эпюры внутренних усилий при кручении
Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.
Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.
Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
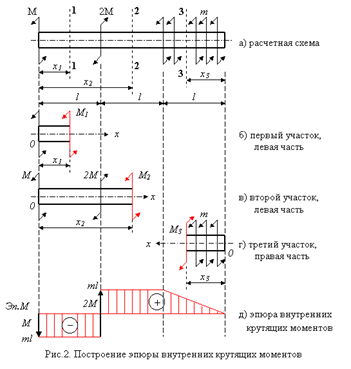
В исходных сечениях № 1,2 и 3 задаются положительными значениями внутренних крутящих моментов М1, М2, М3. Пусть М=ml.
Для первого участка (рис.2 б):
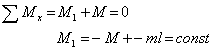
Для второго участка (рис.2 в):
Для третьего участка (рис.2 г):
Границы измерения параметра х3 в следующей системе координат:
Тогда:
Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис.2 д).
4. Эпюры внутренних усилий при прямом изгибе
Ключевые слова: поперечная сила. Внутренний изгибающий момент.
Прямым изгибом называется такой вид простого сопротивления, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствие с конфигурацией поперечного сечения балки.
Как известно, при прямом изгибе в поперечном сечении возникают два вида внутренних усилий: поперечная сила и внутренний изгибающий момент.
Рассмотрим пример расчетной схемы консольной балки с сосредоточенной силой Р, рис. 1, а, но…
Предварительно рекомендую Вам вспомнить из раздела "Статика" теоретической механики методы расчета реакций в связях на примерах тестов, приведенных в ПРИЛОЖЕНИИ по разделом Т-2.
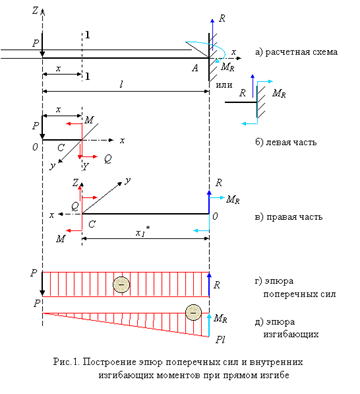
Прежде всего вычислим реакции в связи на базе уравнений равновесия:
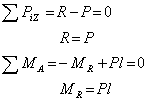
После мысленного рассечения балки нормальным сечением 1-1 рассмотрим равновесие левой отсеченной части (рис.1, б), получим:
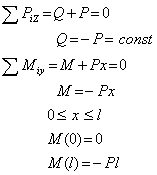
Таким образом, на первом участке поперечная сила отрицательная и постоянная, а внутренний изгибающий момент изменяется по линейному закону.
Для правой отсеченной части при рассмотрении ее равновесия результат аналогичен рис.1, в. А именно:
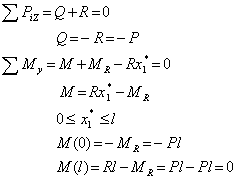
На основании полученных значений строятся эпюры поперечных сил (рис.1, г) и внутренних изгибающих моментов (рис.1, д).
Как следует из построенных эпюр 
, а 
в сечении жесткой связи. Именно это сечение и является наиболее опасным в данной расчетной схеме.
Продифференцируем выражение внутреннего изгибающего момента по координате х:
Как видим, после дифференцирования получено выражение для поперечной силы. Случайность это или закономерность? - Закономерность.
Дифференциальные зависимости между внутренними усилиями при изгибе
Рассмотрим расчетную схему балки с произвольной распределенной нагрузкой 
(рис.2).
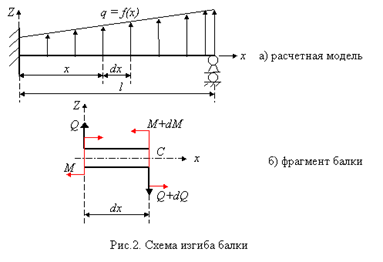
Составим уравнение равновесия:
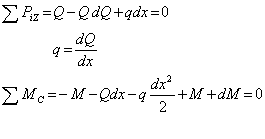
Таким образом, действительно: первая производная от внутреннего изгибающего момента по линейной координате равна поперечной силе в сечении.
Это известное свойство функции и ее первой производной успешно используется при проверке правильности построения эпюр. Так, для расчетной схемы консольной балки (рис.1) эта связь дает следующие проверочные результаты: 
и М убывает от 0 до -Pl. 
и М х.
Таким образом, для квалифицированной проверки Вам рекомендуется вспомнить из высшей математики раздел, связанный с вычислением производных функции. Считаю целесообразно решить тесты, приведенные в ПРИЛОЖЕНИИ под разделом Т-3.
Рассмотрим ВТОРОЙ ХАРАКТЕРНЫЙ ПРИМЕР ИЗГИБА двухопорной балки (рис.3).
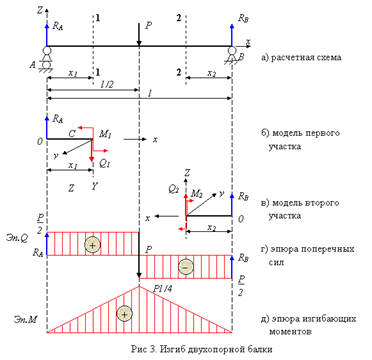
Очевидно, что опорные реакции RA = RB
:
для первого участка (рис.3, б)
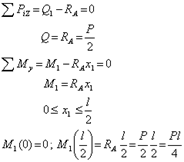
для второго участка (рис.3, в)
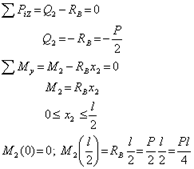
Эпюры внутренних усилий представлены соответственно на рис.3, г и 3, д.
На основе дифференциальной связи Q и М, получим:
для первого участка:
Q > 0 и М возрастает от нуля до 
.
Q = const и M x
для второго участка:
Q < 0 и М убывает с до нуля.
Q = const и M также пропорционален х, т.е. изменяется по линейному закону.
Опасным в данном примере является сечение балки в центре пролета:
Третий характерный пример связан с использованием распределенной по длине балки нагрузки (рис.4). Следуя методике, принятой ранее, очевидно равенство опорных реакций:
,
а для искомого сечения (рис.4, б) выражения для внутренних усилий приобретают вид:
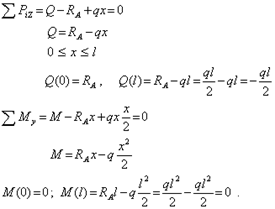
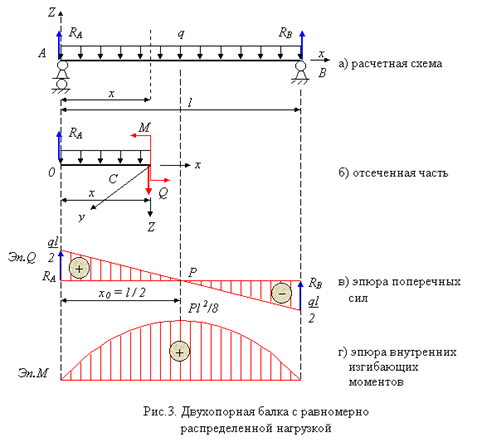
На обеих опорах изгибающий момент отсутствует. Тем не менее опасным сечением балки будет центр пролета при 
. Действительно, исходя из свойства функции и производной при 
, внутренний изгибающий момент достигает экстремума. Для нахождения исходной координаты х0 (рис.3 в) в общем случае приравняем выражение поперечной силы к нулю. В итоге получим
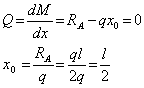
После подстановки в выражение изгибающего момента получим:
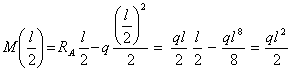
Таким образом,
.
Необходимо отметить, что техника построения эпюр при изгибе наиболее трудно усваивается слушателями. Вам представляется возможность научиться "быстрому" построению эпюр на тесторе-тренажере, приведенном в ПРИЛОЖЕНИИ под грифом Т-4.
Похожие работы
... мощности · Ваттметр · Варметр · Фазометр 2. Основные понятия: сопротивление материалов Сопротивление материалов, наука о прочности и деформируемости элементов (деталей) сооружений и машин. Основные объекты изучения Сопротивление материалов – стержни и пластины, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и ...
... шрифт Times 16пт; «Курский государственный технический университет» - шрифт №5; в компьютерном варианте шрифт Times 14пт; «Кафедра сопротивления материалов и строительной механики» - шрифт №5; в компьютерном варианте шрифт Times 14пт; названию расчетно-графической работы – шрифт №10; в компьютерном варианте Times 18пт; «расчетно-графическая работа №…» - шрифт №7; в компьютерном варианте Times ...
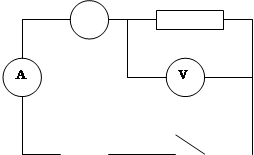
... сечение 1 мм2 Сопротивление проводника зависит не только от материала, из которого он изготовлен, оно зависит и от его размеров длины и поперечного сечения. где - удельное сопротивление l - длина S – площадь поперечного сечения Схема: Оборудование: приборный щит № 1 амперметр 0 – 1А Вольтметр 0 – 150 В Медный провод Æ ...
... . Электропроводность диэлектриков очень мала, так как переход заметного числа электронов в зону проводимости - случайное явление, обусловленное, например, дефектами структуры. Электрическое сопротивление - свойство материалов как проводников противодействовать электрическому току. Вес вещества, помещенные во внешнее магнитное поле, намагничиваются. Намагничивание связано с наличием магнитных ...
0 комментариев