Теория механизмов и машин

1  Структурный и кинематический анализ главного механизма

Выходные данные согласно заданию к курсовому проекту.

1.  Схема двухпоршневого V - образного насоса (рис. 1.1)

2.  Угловая скорость кривошипа , с^-1 16

3.  Погонная единица массы , кг/м 19

4.  Коэффициент () 6,2

5.  Коэффициент (), Н/м 5000

6.  Угол  100

7.  Длина кривошипа , мм 140

8.  Длина шатуна , мм 560

9.  Неравномерность хода  1/5

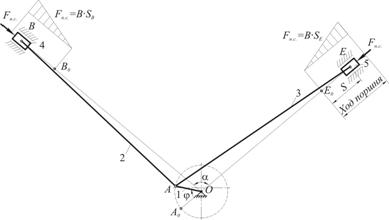
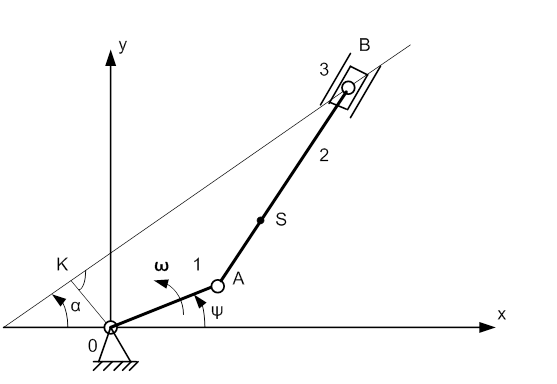
Рис. 1.1. Кинематическая схема механизма

1.1  Структурный анализ механизма

Механизм двухпоршневого горизонтального насоса состоит из 6 звеньев:

1 – кривошип ОА;

2, 3 – шатуны АB и AE;

4, 5 – ползуны (поршни) B и E;

6 – стойка.

Звенья механизма образуют 7 кинематических пар, из которых 5 вращательных и 2 поступательные.

Согласно формуле Чебышева степень свободы определиться как

где  - количество звеньев, ;

  - количество кинематических пар  класса, ;

  - количество пар  класса, .

Таким образом, механизм имеет одну степень свободы.

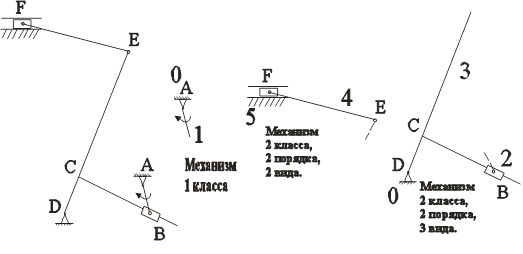
На рис. 1 изображена структурная схема механизма с разбиением на группы Асура и начальный механизм.

Структурная схема наглядно показывает, что механизм состоит из начального механизма 1 класса (стойка 6 и кривошип 1) и двух групп Асура (шатун 2 и ползун 4, шатун 3 и ползун 5).

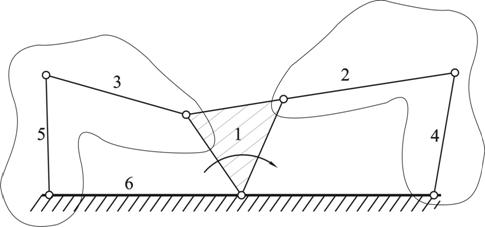
Рис. 1.2 Структурная схема механизма

Структурная формула механизма:

Механизм относится к механизмам II класса по классификации И. И. Артоболевского.

1.2  Построение плана положений механизма

На листе формата А1 изображаем в масштабе план положений механизма. План строим в такой последовательности. Выбираем масштаб построения:

Выбираем произвольную точку О и из нее описываем окружность радиуса ОА. Начальное положение точки А (А_О) выбираем согласно исходной схемы на продолжении направляющей ОE, при пересечении ее с вычерченной окружностью. От точки А_О в направлении вращения кривошипа ОА разбиваем окружность на 12 равных частей, через каждые 30 градусов, проставляя при этом последовательно точки А₁, А₂ и т. д. Соединив полученные точки с центром окружности О, получим 12 положений кривошипа ОА. Точка E принадлежит шатуну АE и ползуну E и движется поступательно по направляющей ОE, поэтому для построения плана положений звена АE из каждой точки А раствором циркуля, равным длине шатуна АE в принятом масштабе, делаем засечки на направляющей, получая точки E₁, E₂ и т. д. План положений для звена AB строим аналогично.

1.3  Построение планов скоростей

Паны скоростей строятся по векторным уравнениям, которые составляются отдельно для каждой группы Асура в порядке присоединения их к ведущему звену.

Для ведущего звена ОА определяем величину скорости точки А:

Вектор  перпендикулярен радиусу, т. е. отрезку ОА, и направлен в сторону, определяемую направлением . Задаемся масштабом плана скоростей

,

и вычисляем отрезок , изображающий в выбранном масштабе вектор

Из произвольной точки Р, называемой полюсом плана скоростей, откладываем в указанном направлении отрезок  длиной 44,8 мм.

Составляем векторное уравнение, по которому определим скорость точки B, принадлежащей шатуну АB и ползуну B.

Скорость точки А известна, скорость относительного вращения точки B вокруг точки А перпендикулярна радиусу вращения отрезку АB и определяется по формуле

.

Скорость точки B направлена вдоль направляющей АB. Таким образом, получаем векторное уравнение, в котором два вектора известны по направлению, но неизвестны по величине, а третий вектор известен по направлению и по величине. Решая это векторное уравнение графическим способом, получим план скоростей для группы Асура, состоящей из звеньев 2 и 4. В соответствии с векторным уравнением через конец вектора  (точку а) проводи направление вектора , перпендикулярное BА, а через полюс  - направление вектора , параллельное АB. На пересечении этих направлений поставим точку B, а отрезки  и в масштабе будут представлять скорости  и . Для определения их величины достаточно измерить соответствующие отрезки и умножить их на масштабный коэффициент :

Пользуясь построенным планом скоростей, можно определить угловую скорость  по формуле:

Для определения направления  переносим вектор  в точку B механизма и рассматриваем движение этой точки относительно точки А по направлению скорости .

Аналогично строим план скоростей для группы Ассура (звенья 3 и 5) по уравнению:

и определяем угловую скорость шатуна AE:

Для определения направления  переносим вектор  в точку E и рассматриваем движение этой точки относительно точки A.

Изложенным выше способом строим планы скоростей для остальных 11 положений.

Результаты построения заносим в таблицу 1.1.

Таблица 1.1

Полож.	0	1	2	3	4	5	6	7	8	9	10	11
, град	0	30	60	90	120	150	180	210	240	270	300	330
[PA], мм	44,80	44,80	44,80	44,80	44,80	44,80	44,80	44,80	44,80	44,80	44,80	44,80
[AВ], мм	8,03	29,34	42,25	44,16	34,77	15,76	8,03	29,34	42,25	44,16	34,77	15,76
[РВ], мм	46,10	39,94	18,94	9,70	34,38	45,80	42,14	28,70	11,71	5,86	23,21	38,40
[AЕ], мм	44,80	39,10	22,94	0,00	22,94	39,10	44,80	39,10	22,34	0,00	22,94	39,10
[РЕ], мм	0,00	17,51	33,83	44,80	43,77	27,29	0,00	27,29	43,77	44,80	33,83	17,51
VAВ, м/с	0,40	1,47	2,11	2,21	1,74	0,79	0,40	1,47	2,11	2,21	1,74	0,79
VВ, м/с	2,30	2,00	0,95	0,48	1,72	2,29	2,11	1,43	0,59	0,29	1,16	1,92
VAЕ, м/с	2,24	1,96	1,15	0,00	1,15	1,96	2,24	1,96	1,12	0,00	1,15	1,96
VЕ, м/с	0,00	0,88	1,69	2,24	2,19	1,36	0,00	1,36	2,19	2,24	1,69	0,88
ВА, с-1	0,72	2,62	3,77	3,94	3,10	1,41	0,72	2,62	3,77	3,94	3,10	1,41
ЕА, с-2	4,00	3,49	2,05	0,00	2,05	3,49	4,00	3,49	2,00	0,00	2,05	3,49

1.4  Построение планов ускорений

Определяем ускорение точки А. Так как кривошип по условию движется равномерно (угловое ускорение равно нулю), то ускорение точки А состоит только из нормальной составляющей, которая равна:

Вектор  направлен по радиусу к центру – от точки А к точке О. Задаемся масштабом плана ускорений  и вычисляем длину отрезка , изображающего в масштабе вектор

Из произвольной точки , называемой полюсом плана ускорений, в направлении вектора  откладываем отрезок .

Переходим к группе Ассура (звенья 2, 4).

Векторное ускорение для точки С группы имеет вид

Ускорение  слагается из нормальной и касательной составляющих

Ускорение  по величине равно

Вычисляем его величину и откладываем в масштабе от точки а плана ускорений в направлении от точки B к точке А механизма отрезок , равный по величине:

Ускорение  определяется по формуле:

Вектор  направлен вдоль направляющей ОB. Таким образом, получаем в векторном уравнении два неизвестных по величине, но известных по направлению вектора. Для их определения продолжим построение плана ускорений. Из точки  плана проведем направление вектора  перпендикулярно BА, а из точки  - параллельно направлению  (параллельно направляющей ОB). На пересечении этих направлений поставим точку b. Получаем отрезки  и , которые в масштабе изображают соответственно ускорение  и , т. е.

 и

Зная , определяем величину углового ускорения :

Направление углового ускорения определится после переноса вектора  в точку B механизма.

Для группы Ассура (звенья 3, 5) построение выполняется аналогично по векторному уравнению:

Строим план ускорений для положения 2.

Строим план ускорений для положения 7.

Результаты построения заносим в таблицу 1.2

Таблица 1.2

Пол.
	м×с-2	м×с-2	м×с-2	с-2	м×с-2	м×с-2	м×с-2	м×с-2	с-2	м×с-2
2	25,41	10,12	27,31	18,08	58,14	2,35	31,27	31,36	55,84	22,4
7	12,25	25,58	28,31	45,68	15,41	6,83	17,48	18,77	31,22	35,63

1.5  Кинематические диаграммы

Диаграммы строятся для 12 положений механизма, которые были изображены на плане положений. Полный оборот кривошипа ОА соответствует одному кинематическому циклу

Рассмотрим построение диаграммы перемещения ползуна В . Проводим координатные оси  и . На оси  откладываем 12 равновеликих отрезков 0-1, 1-2 и т. д., соответствующих углу поворота кривошипа на 1/12 часть оборота (30⁰). Через точки 1, 2, 3 и т. д. проводим ординаты и откладываем на них отрезки, равные координатам токи с -  в соответствующих положениях, отсчитываемых от крайнего нижнего положения точки В. Соединяя полученные точки плавной кривой линией, изображаем диаграмму .

При равномерном вращении кривошипа угол его поворота  пропорционален времени. Поэтому полученная диаграмма  является одновременно диаграммой зависимости перемещения ползуна от времени . Разница будет лишь в масштабах абсцисс.

Масштаб перемещения . Масштаб углов  равен

где  - отрезок (мм) по оси , изображающий полный оборот кривошипа ОА (2p).

Масштаб оси времени  диаграммы равен

,

где Т – период одного оборота кривошипа, который определяется по формуле:

Таким образом, для получения масштаба времени  достаточно разделить масштаб угла поворота  на величину угловой скорости кривошипа .

Построение кривых  и  выполняется способом графического дифференцирования (методом хорд). При этом масштабные коэффициенты диаграмм определяются по формулам:

;

где Н и Н₁ – полюсные расстояния диаграмм соответственно, мм.

Далее стоит построить диаграмму угловых перемещений шатунов АС и BD. Угловое перемещение измеряют в градусах, отсчитывая его от направляющих ОЕ и ОВ.

Поворот против часовой стрелки, относительно оси направляющих ползунов принимаем за положительный. Масштабный коэффициент  определится по формуле:

 или

Выполнив графическое дифференцирование диаграммы углового перемещения, получим диаграмму угловой скорости. Масштабный коэффициент для данной диаграммы

1.6  Сравнение результатов кинематического исследования, выполненного графическим и графоаналитическим методами

Результаты кинематического исследования сводим в таблицу 3.

Таблица 1.3

Положение	0	1	2	3	4	5	6	7	8	9	10	11
, град	0	30	60	90	120	150	180	210	240	270	300	330
VВ, м/с план	2,30	2,00	0,95	0,48	1,72	2,29	2,11	1,43	0,59	0,29	1,16	1,92
VВ, м/с диагр	2,29	2,03	0,93	0,51	1,68	2,29	2,11	1,44	0,58	0,30	1,16	1,92
, %	0,70	-1,65	1,36	-4,91	2,14	-0,04	0,05	-0,48	0,66	-2,72	0,44	0,02
VЕ, м/с план	0,00	0,88	1,69	2,24	2,19	1,36	0,00	1,36	2,19	2,24	1,69	0,88
VЕ, м/с диагр	0,00	0,86	1,70	2,23	2,23	1,32	0,00	1,31	2,23	2,23	1,70	0,86
, %	0	1,37	-0,35	0,42	-1,93	3,41	0	3,86	-1,85	0,42	-0,35	1,37
ВА, с-1 план	0,72	2,62	3,77	3,94	3,10	1,41	0,72	2,62	3,77	3,94	3,10	1,41
ВА, с-1 диагр	0,68	2,59	3,73	3,88	3,08	1,38	0,71	2,59	3,73	3,99	3,08	1,40
, %	5,11	0,98	1,10	1,49	0,73	1,67	1,49	1,06	1,08	-1,22	0,79	0,53
ЕА, с-1 план	4,00	3,49	2,05	0,00	2,05	3,49	4,00	3,49	2,00	0,00	2,05	3,49
ЕА, с-1 диагр	3,96	3,46	2,03	0,00	2,02	3,44	3,95	3,46	0,23	0,00	2,03	3,55
, %	1,10	0,82	1,05	0,00	1,54	1,36	1,33	0,82	88,42	0,00	0,86	-1,53
aB план , м/с2	-	-	58,14	-	-	-	-	15,41	-	-	-	-
aB диагр , м/с2	2,76	26,54	48,37	42,69	33,94	2,48	14,60	21,03	25,53	26,39	26,77	18,99
, %	-	-	-16,79	-	-	-	-	36,49	-	-	-	-
aE план , м/с2	-	-	22,40	-	-	-	-	35,63	-	-	-	-
aE диагр , м/с2	28,18	26,65	21,68	8,18	10,54	33,94	48,65	33,94	10,54	8,18	21,68	26,65
, %	-	-	-3,18	-	-	-	-	-4,72	-	-	-	-

Расхождение результатов не превышает 5%

Превышение 5% в расхождении значений ускорений точки В объясняется погрешностью при выполнении графического дифференцирования.

2  Кинематический анализ кулачкового механизма 2.1  Построение плана положений

Задан кулачковый механизм (рис. 2.1) с размерами:

1.  Радиус  24

2.  Радиус  36

3.  Радиус  24

4.  Расстояние  12

5.  Длина  80

6.  Расстояние  100

7.  Угловая скорость  10

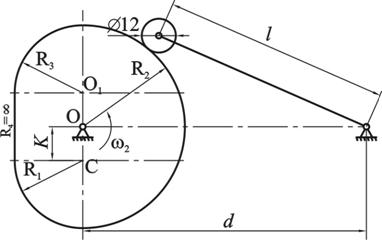
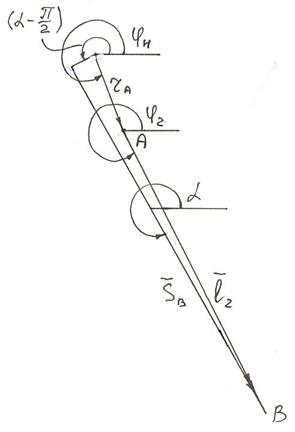
Рис. 2.1 Кинематическая схема кулачкового механизма

В соответствии с исходными данными строим в масштабе кулачек, масштабный коэффициент при этом выбираем .

Задача анализа кулачкового механизма сводится к определению положений толкателя в зависимости от положения кулачка и установлению скоростей и ускорений толкателя. Для кулачкового механизма с вращательным движением толкателя, снабженным роликом, задача об определении положения и перемещения толкателя решается следующим образом.

Центр вращения ролика всегда находится от действительного профиля кулачка на расстоянии, равном радиусу ролика . Геометрическое место точек, через которые будет проходить центр вращения ролика, образует собой центровой профиль кулачка. Для определения положения толкателя применяем метод обращения, т.е. кулачек оставляем неподвижным, а толкатель вместе со стойкой поворачиваем на заданный угол  относительно оси вращения кулачка в направлении, противоположном его вращению. Радиусом  из центра вращения кулачка проводим окружность – геометрическое место точек положений центра вращения толкателя. Для определения положения центра вращения толкателя для нулевого положения, на центровом профиле берем точку наиболее приближенную к оси кулачка и радиусом  проводим еще одну окружность. на пересечении получаем центр вращения толкателя для нулевого положения (точка 0). Окружность радиусом  от точки 0 делим на равные части по 15 градусов, получая точки 1, 3, 4, 5, 6, 7….. Проводим из этих точек окружности радиусом . Они будут пересекать центровой профиль кулачка в точках, в которых будет находиться центр ролика толкателя для соответствующих положений. Измеряем углы между отрезками длиной  и  получаем углы ,  и т. д.

Дополнительно берем точки 2, 8, 9, 14, соответствующие моменту перехода ролика от одного участка кулачка к другому (Под участком понимаем часть профиля кулачка с одинаковым законом изменения профиля). Угловое перемещение толкателя буде определять как разность углов произвольного  и начального  положения:

Линейное перемещение ролика будет пропорционально угловому перемещению:

2.2  Построение диаграммы перемещений толкателя

Диаграмма перемещений толкателя строится следующим образом.

Строим систему координат. По оси ординат откладываем перемещения толкателя. По оси абсцисс будем откладывать угловое перемещение кулачка, масштабный коэффициент равен .

Масштабный коэффициент перемещения толкателя

2.3  Построение диаграмм скорости и ускорения толкателя.

Диаграмма скорости толкателя строится путем графического дифференцирования диаграммы перемещения методом хорд. Масштабный коэффициент диаграммы скорости толкателя:

где  - отрезок, соответствующий полному обороту кулачка

 - полюсное расстояние диаграммы скорости.

Диаграмма ускорения строится методом графического дифференцирования диаграммы скорости. Масштабный коэффициент диаграммы ускорения равен

Для получения величины скорости необходимо ординату диаграммы скорости умножить на масштабный коэффициент. Для получения величины ускорения толкателя необходимо ординату диаграммы ускорения умножить на масштабный коэффициент.

2.4  Построение диаграммы изменения угла давления.

Угол давления – это угол между вектором скорости толкателя и нормалью к точке касания толкателя и кулачка. Для каждого положения кулачка измеряем угол давления и строим зависимость угла давления от угла поворота кулачка. Масштабный коэффициент

3  Кинематический анализ сложного зубчатого механизма 3.1  Выходные данные

Задана схема сложного зубчатого механизма, показанная на рисунке 3.1, для которой в таблице 3.1 представлены выходные данные: число зубьев, модуль зацепления, угловая скорость колеса 1 и радиусы колес, вычисленные по формуле:

,

где  - количество зубьев колес (табл. 3.1);

  - модуль зуба колеса (табл. 3.1).

Рис. 3.1

Определим незаданные размеры колес и водил

Таблица 3.1

№ колеса	Число зубьев,	Модуль зуба , мм	Угловая скорость колеса 1 , 1/с	Радиус колеса,  мм
1	17	3	3	25,5
2	34			51
2’	16			24
3	35			52,5
4				76,5
4’	25			37,5
5	30			45
5’	20			30
6	35			52,5
7				82,5
7’	30			45
8	36			54

Изображаем схему механизма в масштабе

3.2  Кинематический анализ сложного зубчатого механизма, выполненный аналитическим способом

Схема зубчатого редуктора состоит из нескольких ступеней – двух планетарных редукторов Давида и пары с неподвижными осями. Передаточное отношение первого планетарного механизма Давида определяем от колеса 1 до водила 4.

где  - передаточное отношение от 1 колеса к колесу 3 при неподвижном водиле 4.

Передаточное отношение второго планетарного механизма Давида определяем от колеса 4’ до водила 7.

Передаточное отношение зубчатой пары 7’ – 8

Передаточное отношение редуктора

3.3  Кинематический анализ сложного зубчатого механизма, выполненный графическим способом

Проводим снизу от схемы редуктора горизонтальную прямую. Вдоль оси  проводим вертикальную линию до пересечения с горизонтальной прямой. На пересечении получаем точку .

Проводим из точки А колеса 1 вертикальную линию до пересечения с горизонтальной прямой. От точки пересечения перпендикулярно откладываем в масштабе  вектор скорости точки А ():

Соединяем конец вектора  с точкой , получаем картину распределения скоростей колеса 1. Для построения картины распределения скоростей для колес 2 и 2’ соединяем конец вектора  с точкой . Для нахождения скорости точки , на уровне точки восстанавливаем перпендикуляр к горизонтальной прямой до пересечения с прямой . Величина перпендикуляра в масштабе дает нам модуль скорости.

Аналогично определяем законы распределения скоростей для остальных колес.

Для построения плана угловых скоростей проведем две линии: горизонталь и вертикаль. На вертикальной линии отложим масштабе значение угловой скорости первого колеса  (точка 1). Из точки 1 проводим прямую, параллельную линии  (линии, выражающей закон распределения скоростей для первого колеса). На пересечении этой линии с горизонтальной прямой получим полюс построения Н. Проводим из полюса прямые параллельные линиям, выражающим законы распределения скоростей для всех колес, и получаем в пересечении с горизонтальной прямой точки 2, 3 и т. д. Отрезки [01], [02] и т. д. будут в масштабе давать угловые скорости колес.

Масштабный коэффициент

Определяем угловые скорости колес. Данные расчета приведены в таблице 3.2

Передаточное отношение редуктора определим из плана угловых скоростей

Таблица 3.2

Колесо	Отрезок, мм	Угловая скорость, с-1
1	150	3
2	141,66	2,8332
4	44,44	0,8888
5	111,11	2,2222
7	40,4	0,808
8	33,67	0,6734

3.4  Сравнение результатов кинематического анализа

Сравниваем передаточные отношения, найденные аналитическим и графическим способами.

3.5  Синтез эвольвентного зацепления

Нарезание эвольвентных профилей зубьев методом обкатки наиболее распространенный способ изготовления зубчатых колес

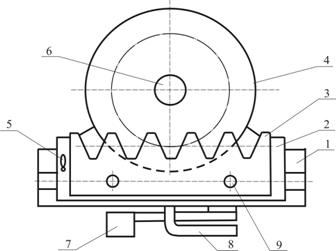
Рис. 3.2

Общий вид приспособления ТММ – 42 для вычерчивания профиля зубьев методом обкатки показан на рисунке 3.2. Основание 1 имеет паз для перемещения подвижной планки 2, на которой винтами 9 фиксируется рейка 3 и ось, вокруг которой поворачивается соединенные между собой два диска 4. Нижний диск имеет диаметр делительной окружности нарезаемого колеса. Концы стального троса, охватывающего диск, закреплены на подвижной планке. Натяжение троса обеспечивается с помощью рычага 5. На верхнем диске прижимной шайбой 6 закрепляется бумажный диск, имитирующий заготовку. Прерывистое перемещение рейки относительно заготовки обеспечивается храповым механизмом путем нажимом на клавишу 7. при каждом нажатии рейка перемещается влево на один шаг. Поворачивая рычаг 8 против часовой стрелки можно освободить подвижную планку от храпового механизма и перемещать ее вручную вправо или влево. Другое движение планки - радиальное. Это перемещение отсчитывается по шкале на планке и фиксируется винтами 9.

Сначала подготавливаем бумажный диск заготовку и устанавливаем его в устройстве, фиксируя прижимной гайкой.

Устанавливаем риски рейки напротив нулевого значения шкалы. Поворачивая рычаг 8, освобождаем планку от храпового механизма, переводим ее в крайнее правое положение и закрепляем. Рычагом 5 ослабляем натяжение троса и поворачиваем диск таким образом, что бы левый крайний зуб рейки совпадал с началом первого сектора заготовки и закрепляем трос.

Обрисовываем карандашом профиль зубьев рейки. Нажимая клавишу 7, переводим рейку влево на один шаг и снова обрисовываем профиль зубьев. Продолжаем так делать, пока рейка не дойдет до конца влево.

Для второго сектора смещаем рейку на 10 мм вниз ().

Для третьего сектора смещаем рейку на 10 мм вверх ().

Для исключения подрезания зуба находим относительный () и абсолютный  сдвиг рейки. Количество зубьев .

Для четвертого сектора устанавливаем смещение планки на  и прорисовываем профиль зубьев.

Снимаем заготовку и в каждом секторе наносим по 4 окружности:

 - радиус делительной окружности

 - радиус основной окружности;

 - радиус окружности выступов;

 - радиус окружности впадин.

Определяем шаг по делительной окружности

4  Кинетостатический (силовой) анализ главного механизма 4.1  Выходные данные

Выходные данные согласно заданию к курсовому проекту.