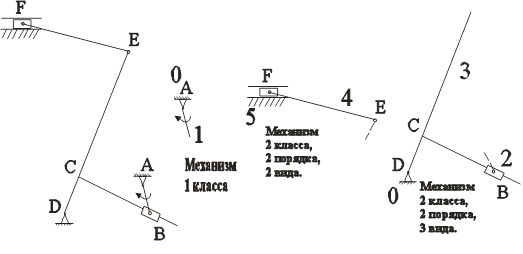
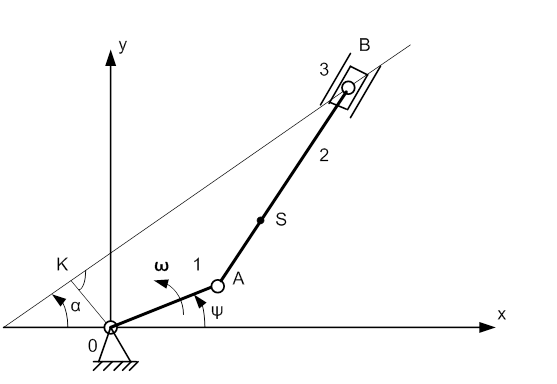
Схема двухпоршневого V - образного насоса (рис. 1.1)

1.  Схема двухпоршневого V - образного насоса (рис. 1.1)

2.  Угловая скорость кривошипа , с^-1 16

3.  Погонная единица массы , кг/м 19

4.  Коэффициент () 6,2

5.  Коэффициент (), кН/м 5

6.  Длина кривошипа , мм 140

7.  Длина шатуна , мм 560

8.  Неравномерность хода  1/5

Задачей силового исследования является определение реакций в кинематических парах механизма, находящегося под действием внешних сил. Закон движения при этом считается заданным. Для того, что бы ведущее звено двигалось по заданному закону, необходимо к нему приложить так называемую уравновешивающую силу (или уравновешивающий момент), которая уравновешивает все силы и силы инерции. Определение уравновешивающей силы или уравновешивающего момента наряду с определением реакций в кинематических парах так же является задачей силового исследования механизма.

Силовой расчет выполняется в порядке, обратном кинематическому исследованию, т. е. сначала ведется расчет группы Ассура, наиболее удаленной от начального механизма, затем предыдущей и т. д., и, наконец, начального механизма.

4.2  Определение действующих сил и сил инерции

Определяем массу звеньев.

Масса кривошипа АВ (с):

.

Масса шатунов АС и ВD ( и )

.

Масса ползунов С и D ( и ):

.

Вес звеньев:

.

Центрами масс для линейных звеньев считаем середины межшарнирных расстояний, а для ползунов – точки С и D.

Сила полезного сопротивления возникает при сопротивлении ползунов нагнетанию. Противоположное направление движение ползунов является холостым ходом. Для положения 2 механизма силs полезного сопротивления будут равны

где  - коэффициент;

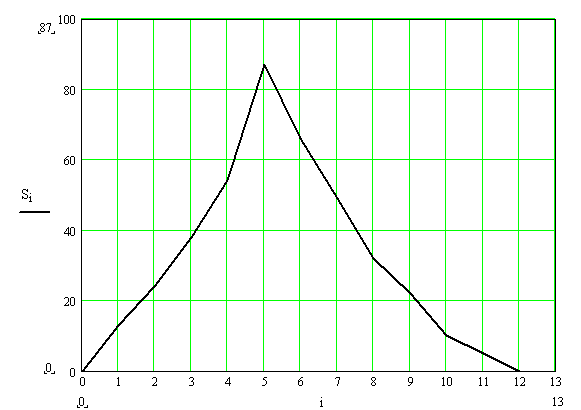
,  - перемещение ползунов для положения 2. Из диаграммы перемещений

,

Силы инерции в общем случае рассчитываются по формуле

где  - ускорение центра тяжести звена. Из плана ускорений

; ; ; ;

Момент инерции не равен нулю будет для шатунов 2 и 3.

где  - осевой момент инерции шатуна, относительно оси, проходящей через центр тяжести.

 - угловое ускорение шатуна.

Направление сил инерции противоположно направлению ускорений.

4.3  Силовой расчет группы Ассура без учета сил трения 4.3.1  Звенья 2-4.

Изображаем отдельно группу Ассура, нагруженную действующими силами и силами инерции. Отсоединив звено 2 от стойки 6 и кривошипа 1, прикладываем в точках А и B силы  и  - силы реакций в кинематических парах 1-2 и 4-6.

Кинематическая пара 1-2 – вращательная, поэтому раскладываем ее на две составляющие

Реакция в поступательной паре 4-6 неизвестна по величине, но известна по направлению; направлена перпендикулярно движению.

Определяем величину касательной составляющей, для чего составляем для звена 2 уравнение моментов относительно точки С.

Откуда

где ; ; .

Векторная сумма всех сил, действующих на группу Ассура, включая и силы инерции, равна нулю, т. е.

В этом уравнении два вектора  и  известны только по направлению, остальные известны полностью, следовательно, уравнение решается.

В соответствии с последним векторным уравнением строим так называемый план сил. Для этого выбираем масштаб построения . Из произвольной точки в выбранном масштабе откладываем все известные векторы в той последовательности, которая указана в уравнении равновесия. Через начало первого вектора проводим направление нормальной составляющей , а через конец последнего – направление реакции . Пересечение этих направлений определяет величины отрезков, изображающих в масштабе векторы неизвестных реакций. Складывая на плане сил нормальную и тангенциальную составляющие, получаем полную реакцию

Для определения реакции в кинематической паре 2-4 составляем уравнение равновесия звена 2, записанное в виде векторной суммы всех сил:

Используем уже построенный план сил, на котором соединяем начало вектора  с концом вектора . Направлена искомая реакция из конца последнего вектора в начало первого.

Умножая полученные отрезки на масштабный коэффициент, получаем:

4.3.2  Звенья 3-5

Изображаем отдельно группу Ассура, нагруженную действующими силами и силами инерции. Отсоединив звено 3 от стойки 6 и кривошипа 1, прикладываем в точках А и Е силы  и  - силы реакций в кинематических парах 1-3 и 6-5.

Кинематическая пара 1-3 – вращательная, поэтому раскладываем ее на две составляющие

Реакция в поступательной паре 5-6 неизвестна по величине, но известна по направлению; направлена перпендикулярно движению.

Определяем величину касательной составляющей, для чего составляем для звена 3 уравнение моментов относительно точки Е.

Откуда

Векторная сумма всех сил, действующих на группу Ассура, включая и силы инерции, равна нулю, т. е.

В этом уравнении два вектора  и  известны только по направлению, остальные известны полностью, следовательно, уравнение решается.

В соответствии с последним векторным уравнением строим так называемый план сил. Для этого выбираем масштаб построения . Из произвольной точки в выбранном масштабе откладываем все известные векторы в той последовательности, которая указана в уравнении равновесия. Через начало первого вектора проводим направление нормальной составляющей , а через конец последнего – направление реакции . Пересечение этих направлений определяет величины отрезков, изображающих в масштабе векторы неизвестных реакций. Складывая на плане сил нормальную и тангенциальную составляющие, получаем полную реакцию

Для определения реакции в кинематической паре 3-5 составляем уравнение равновесия звена 3, записанное в виде векторной суммы всех сил:

Используем уже построенный план сил, на котором соединяем начало вектора  с концом вектора . Направлена искомая реакция из конца последнего вектора в начало первого.

4.4  Силовой расчет начального механизма

На ведущее звено действуют вес кривошипа , реакции  и , сила инерции . В точке О действует реакция со стороны стойки, которую и надо определить.

Ведущее звено под действием заданных сил не будет находиться в равновесии, поэтому необходимо приложить уравновешивающую силу , обеспечивающую движение по заданному закону.

Составим уравнение моментов относительно точки О и определяем величину уравновешивающей силы:

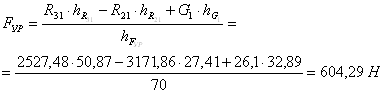
Для определения реакции в кинематической паре кривошип-стойка составляем уравнение равновесия

4.5  Определение уравновешивающего момента с помощью рычага Н.Е. Жуковского.

Уравновешивающий момент может быть определен при помощи теоремы Н. Е. Жуковского о «жестком рычаге», согласно которой сумма моментов всех сил, действующих на механизм, включая силы инерции, перенесенных параллельно самим себе в одноименные точки повернутого на 90⁰ плана скоростей, относительно полюса, равна нулю.

Таким образом, план скоростей представляется как жесткий рычаг, шарнирно закрепленный в полюсе и находящийся под действием сил в равновесии.

По теореме Жуковского легко определить уравновешивающий момент.

Решение проводим в такой последовательности:

1.  Строим в масштабе повернутый на 90⁰ план скоростейб механизма.

2.  По теореме подобия находятся на плане скоростей все точки, в которых приложены все действующие силы. Моменты сил при этом раскладываются на пары сил таким образом, что бы звено, к которому они приложены, представляло собой плечо этой пары.

4.6  Сравнение уравновешивающих моментов, найденных двумя методами

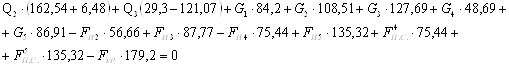
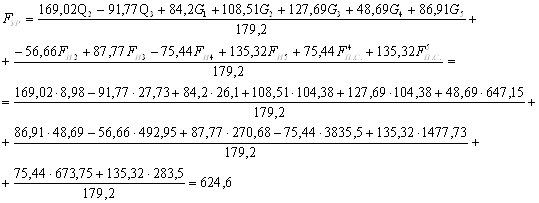
Уравновешивающий момент, определенный по методу Ассура

Уравновешивающий момент, определенный по методу Жуковского

Ошибка составляет

Ошибка не превышает 5%. Расчет сделан правильно.

4.7  Определение сил трения

Определение сил трения

где  - коэффициент трения в поступательной паре, зависит от пары работающих материалов, состояния поверхности, условий смазки и т.д. Для пары материалов «Сталь-сталь» принимаем коэффициент трения

 - реакция в поступательной паре, предварительно определенная без учета сил трения.

Сила трения направлена в сторону, противоположную относительному движению звена.

Возникающий во вращательной паре момент трения рассчитывается по формуле

где  - радиус цапфы подшипника;

 - коэффициент трения для приработавшихся цапф

4.8  Силовой расчет групп Ассура с учетом сил трения 4.8.1  Звенья 2-4

Определяем величину касательной составляющей, для чего составляем для звена 2 уравнение моментов относительно точки С.

Откуда

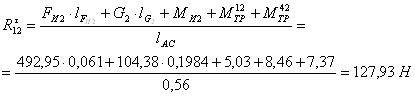
Векторная сумма всех сил, действующих на группу Ассура, включая и силы инерции, равна нулю, т. е.

В этом уравнении два вектора  и  известны только по направлению, остальные известны полностью, следовательно, уравнение решается.

В соответствии с последним векторным уравнением строим так называемый план сил. Для этого выбираем масштаб построения . Из произвольной точки в выбранном масштабе откладываем все известные векторы в той последовательности, которая указана в уравнении равновесия. Через начало первого вектора проводим направление нормальной составляющей , а через конец последнего – направление реакции . Пересечение этих направлений определяет величины отрезков, изображающих в масштабе векторы неизвестных реакций. Складывая на плане сил нормальную и тангенциальную составляющие, получаем полную реакцию

Для определения реакции в кинематической паре 2-4 составляем уравнение равновесия звена 2, записанное в виде векторной суммы всех сил:

Используем уже построенный план сил, на котором соединяем начало вектора  с концом вектора . Направлена искомая реакция из конца последнего вектора в начало первого.

Умножая полученные отрезки на масштабный коэффициент, получаем:

4.8.2  Звенья 3-5

Определяем величину касательной составляющей, для чего составляем для звена 3 уравнение моментов относительно точки С.

Откуда

Векторная сумма всех сил, действующих на группу Ассура, включая и силы инерции, равна нулю, т. е.

В этом уравнении два вектора  и  известны только по направлению, остальные известны полностью, следовательно, уравнение решается.

В соответствии с последним векторным уравнением строим так называемый план сил. Для этого выбираем масштаб построения . Из произвольной точки в выбранном масштабе откладываем все известные векторы в той последовательности, которая указана в уравнении равновесия. Через начало первого вектора проводим направление нормальной составляющей , а через конец последнего – направление реакции . Пересечение этих направлений определяет величины отрезков, изображающих в масштабе векторы неизвестных реакций. Складывая на плане сил нормальную и тангенциальную составляющие, получаем полную реакцию

Для определения реакции в кинематической паре 3-5 составляем уравнение равновесия звена 3, записанное в виде векторной суммы всех сил:

Используем уже построенный план сил, на котором соединяем начало вектора  с концом вектора . Направлена искомая реакция из конца последнего вектора в начало первого.

4.9  Силовой расчет начального механизма

Составим уравнение моментов относительно точки О и определяем величину уравновешивающего момента:

Для определения реакции в кинематической паре кривошип-стойка составляем уравнение равновесия

5  Динамический анализ механизма. Подбор маховика 5.1  Определение приведенных моментов движущих сил и полезного сопротивления

Приведенный момент сил полезного сопротивления для 12 положений механизма находим по формуле

Где  - сила полезного сопротивления для конкретного положения механизма, определяемая зависимостью изменения сил полезного сопротивления от перемещений и  поршней, которая задается в задании на курсовое проектирование;

;

 ,  - скорости поршней, к которым приложена сила полезного сопротивления. Данные скорости определены во время выполнения кинематического анализа механизма;

  - угловая скорость кривошипа. Данная скорость задана заданием курсового проектирования

Результаты расчетов заносим в таблицу 5.1.

Таблица 5.1

Полож.	0	1	2	3	4	5	6	7	8	9	10	11
F4п.с. Н	735,37	1098,12	1347,53	0,00	0,00	0,00	0,00	0,00	0,00	8,00	127,38	382,23
F5п.с. Н	0,00	71,82	283,59	611,09	983,59	1284,26	1400,00	0,00	0,00	0,00	0,00	0,00
V4, м/с	2,30	2,00	0,95	0,48	1,72	2,29	2,11	1,43	0,59	0,29	1,16	1,92
V5, м/с	0,00	0,88	1,69	2,24	2,19	1,36	0,00	1,36	2,19	2,24	1,69	0,88
1, с-1	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00
Mci, Нм	105,93	140,98	109,72	85,55	134,52	109,52	0,00	0,00	0,00	0,15	9,24	45,86

Строим график зависимости приведенного момента сил полезного сопротивления от угла поворота кривошипа, принимая масштабные коэффициенты:

5.2  Определение работы сил полезного сопротивления и движущих сил

Наиболее простой способ определения работы сил полезного сопротивления и движущих сил – это метод графического интегрирования графика зависимости момента сил полезного сопротивления от угла поворота кривошипа. Для этого слева от начала координат откладываем произвольный отрезок длиной , который назавем полюсным расстоянием. Определяем величину моментов  на серединах отрезков ,  и т. д., расположенных на оси . Эти значения проецируем на ось моментов и последовательно соединяем с концом отрезка . Получаем наклонные отрезки, угол наклона которых соответствует наклону хорд на графике работ , который строим под первым графиком. Масштабный коэффициент  зависит от величины полюсного расстояния и определяется по формуле

Момент движущих сил будем считать постоянным, поэтому график зависимости  будет иметь вид наклонной линии, которая начинается в начале координат и заканчивается в последней точке графика , так как работа движущих сил и сил полезного сопротивления в начале и в конце рабочего цикла одинакова.

На графике  покажем график изменения приведенного момента движущих сил . Для этого через конец полюсного расстояния проведем прямую, параллельную графику , до пересечения с осью моментов. На оси получим отрезок, в масштабе равный величине постоянного момента движущих сил .

5.3  Графическое определение изменений кинетической энергии

Изменения кинетической энергии  удобно находить графическим методом.

В новой системе координат  для каждого положения механизма откладываем разницу между работой движущих сил и сил полезного сопротивления.

5.4  Определение приведенного момента инерции механизма для рабочего цикла

Приведенным моментом инерции называется такой условный момент инерции, приложенный к звену приведения, который имеет кинетическую энергию такую же, как и кинетическая энергия всех звеньев.

Звеном приведения является кривошип, кинетическая энергия которого определиться как

Кинетические энергии других звеньев находят в зависимости от вида движения, который они выполняют.

Для вращательного движения

Для поступательного движения

Для двухпоршневого горизонтального насоса можно записать следующее уравнение определения приведенного момента инерции

 

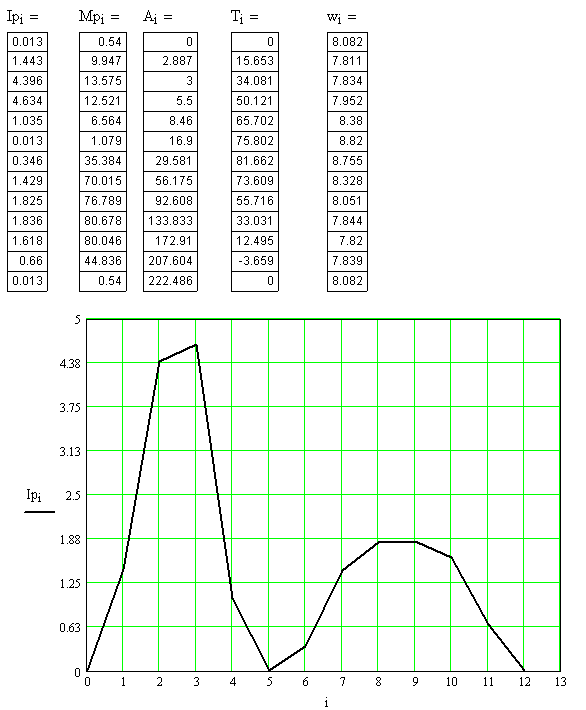
По полученным данным строим график  в масштабе

Исходные данные и результаты расчетов приведены в таблице 5.2

Таблица 5.2

Полож.	0	1	2	3	4	5	6	7	8	9	10	11
m1	2,66	2,66	2,66	2,66	2,66	2,66	2,66	2,66	2,66	2,66	2,66	2,66
m2=m3	10,64	10,64	10,64	10,64	10,64	10,64	10,64	10,64	10,64	10,64	10,64	10,64
m4=m5	65,97	65,97	65,97	65,97	65,97	65,97	65,97	65,97	65,97	65,97	65,97	65,97
l1	0,14	0,14	0,14	0,14	0,14	0,14	0,14	0,14	0,14	0,14	0,14	0,14
l2	0,56	0,56	0,56	0,56	0,56	0,56	0,56	0,56	0,56	0,56	0,56	0,56
1	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00	16,00
2	0,72	2,62	3,77	3,94	3,10	1,41	0,72	2,62	3,77	3,94	3,10	1,41
3	4,00	3,49	2,05	0,00	2,05	3,49	4,00	3,49	2,00	0,00	2,05	3,49
V2	2,26	1,99	1,36	1,19	1,80	2,23	2,17	1,73	1,25	1,15	1,56	2,05
V3	1,12	1,39	1,90	2,24	2,14	1,58	1,12	1,58	2,14	2,24	1,90	1,39
V4	2,30	2,00	0,95	0,48	1,72	2,29	2,11	1,43	0,59	0,29	1,16	1,92
V5	0,00	0,88	1,69	2,24	2,19	1,36	0,00	1,36	2,19	2,24	1,69	0,88
12	256	256	256	256	256	256	256	256	256	256	256	256
22	0,51	6,86	14,23	15,55	9,64	1,98	0,51	6,86	14,23	15,55	9,64	1,98
32	16,00	12,19	4,20	0,00	4,20	12,19	16,00	12,19	3,98	0,00	4,20	12,19
V22	5,12	3,96	1,84	1,41	3,23	4,98	4,69	3,00	1,56	1,33	2,43	4,20
V32	1,25	1,94	3,61	5,02	4,57	2,48	1,25	2,48	4,57	5,02	3,61	1,94
V42	5,31	3,99	0,90	0,24	2,96	5,24	4,44	2,06	0,34	0,09	1,35	3,69
V52	0,00	0,77	2,86	5,02	4,79	1,86	0,00	1,86	4,79	5,02	2,86	0,77
IП	1,67	1,51	1,23	1,65	2,35	2,17	1,43	1,28	1,61	1,61	1,37	1,43

5.5  Методика построения диаграммы энергомасс (кривой Виттенбауэра) и нахождения по ней момента инерции маховика

Диаграмму энергомасс (зависимость ) строят по точкам, используя уже построенные диаграммы изменений кинетической энергии механизма и приведенного момента инерции. Значения этих параметров можно брать из графиков без изменений.

К кривой Виттенбауэра проводят две касательные сверху и снизу. Углы наклона этих линий определяют по формулам:

где  - квадрат средней скорости кривошипа;

 - заданный коэффициент неравномерности хода.

Касательно к диаграмме под углом  к горизонтали проводим сверху, а под углом  - снизу.

Данные касательные пересекут ось  в точках А и В. Измеряем величину отрезка  и находим момент инерции маховика.

5.6  Определение конструктивных размеров маховика

Маховик выполняется, как колесо с массивным ободом. Пренебрегая массой спиц и ступицы, имеем:

,

где  - масса обода, кг;

 - средний диаметр обода, м.

Расчет будем проводить методом последовательных приближений. В первом приближении конструктивно задаемся средним диаметром  в пять раз большим длины кривошипа

,

тогда

Массу маховика выражаем через его размеры

,

где  - удельный вес материала маховика (чугун).

Обычно принимают величину  (рис. 5.1), тогда

Откуда находим

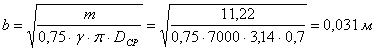
Полученный размер должен ориентировочно равен

Условие не выполняется, поэтому изменяем  до 0,35 м

Рис. 5.1

Условие выполняется. Находим остальные размеры.

5.7  Определение угловой скорости кривошипа за цикл

Определяем угловую скорость кривошипа в зависимости от угла поворота:

где , - значение приведенного момента инерции и изменения кинетической энергии в точке, где касательная, проведенная под углом , касается кривой Виттенбауэра;

,  - текущие значения приведенного момента инерции и изменения кинетической энергии, которые снимаются с диаграммы Виттенбауэра;

- определяется по формуле:

=

Результаты расчетов сведены в таблицу

Таблица 5.3

Полож.	0	1	2	3	4	5	6	7	8	9	10	11
I	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
T	1,14	1,14	1,14	1,14	1,14	1,14	1,14	1,14	1,14	1,14	1,14	1,14
[IП]	33,39	30,17	24,65	33,10	47,05	43,48	28,53	25,53	32,29	32,27	27,35	28,70
IП	1,67	1,51	1,23	1,65	2,35	2,17	1,43	1,28	1,61	1,61	1,37	1,43
T]	0,00	-9,26	-18,79	-24,17	-31,41	-40,44	-39,39	-30,13	-20,86	-11,59	-3,03	2,10
T	0,00	-10,58	-21,47	-27,62	-35,90	-46,22	-45,02	-34,43	-23,84	-13,25	-3,47	2,40
IП max=IП1	1,23	1,23	1,23	1,23	1,23	1,23	1,23	1,23	1,23	1,23	1,23	1,23
Tmax=T1	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58	-10,58
CP	16	16	16	16	16	16	16	16	16	16	16	16
	1/5	1/5	1/5	1/5	1/5	1/5	1/5	1/5	1/5	1/5	1/5	1/5
2max	307,2	307,2	307,2	307,2	307,2	307,2	307,2	307,2	307,2	307,2	307,2	307,2
Iмахов	1,37	1,37	1,37	1,37	1,37	1,37	1,37	1,37	1,37	1,37	1,37	1,37
i	16,43	16,66	17,28	15,90	14,18	14,33	16,16	16,85	16,09	16,31	17,23	17,15

Определив для 12 положений угловую скорость кривошипа строим график зависимости . На графике показываем значения  и .

Литература

 

1.  Артоболевский И.И., Теория механизмов и машин.- М.: Наука, 1975.

2.  Баранов Г.Г. Курс теории механизмов и машин.- М.: Машиностроение, 1967.- 170 с.

3.  Кореняко А.С. Курсовое проектирование по теории механизмов и машин. - Киев: Вища школа,1975. – 153 с.

4.  Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин.- М.: Машиностроение, 1985. – 291 с.