САПР FOUNDATION
ВИДЫ АППРОКСИМАЦИИ ЧАСТОТНЫХ ХАРАКТЕРИСТИК: АППРОКСИМАЦИЯ ЧЕБЫШЕВА (ПРЯМАЯ И ИНВЕРСНАЯ)
АППРОКСИМАЦИЯ ЧЕБЫШЕВА ИНВЕРСНАЯ (ВТОРОГО РОДА)
РАЗРАБОТКА ПРИНЦИПИАЛЬНОЙ СХЕМЫ ФИЛЬТРА, РАСЧЕТ ЭЛЕМЕНТОВ
МОДЕЛИРОВАНИЕ ФИЛЬТРА НА СХЕМАТЕХНИЧЕСКОМ УРОВНЕ В СИСТЕМЕ ELECTRONIC WORKBENCH В ЧАСТОТНОЙ И ВРЕМЕННОЙ ОБЛАСТЯХ (ИЗМЕРЕНИЕ АЧХ, ФЧХ, ЧРЗ, ИХ, ПХ)
Навигация
ВИДЫ АППРОКСИМАЦИИ ЧАСТОТНЫХ ХАРАКТЕРИСТИК: АППРОКСИМАЦИЯ ЧЕБЫШЕВА (ПРЯМАЯ И ИНВЕРСНАЯ)
Проектирование устройств фильтрации
44493
знака
3
таблицы
33
изображения
3. ВИДЫ АППРОКСИМАЦИИ ЧАСТОТНЫХ ХАРАКТЕРИСТИК: АППРОКСИМАЦИЯ ЧЕБЫШЕВА (ПРЯМАЯ И ИНВЕРСНАЯ)
Задача аппроксимации состоит в том, чтобы синтезировать некоторую функцию частоты, удовлетворяющую требованиям к АЧХ или ХРЗ разрабатываемого фильтра. Наиболее удобно функцию частоты представить в виде ХРЗ
(3.1)
где ε^2 – коэффициент, характеризующий степень постоянства (неравномерность) затухания (усиления) в полосе пропускания; ψ(ω) – функция фильтрации, для которой желательны значения, близкие к нулю в полосе пропускания и как можно большие в полосе задерживания. Функция фильтрации в общем случае может быть дробной.[3]
В качестве функции фильтрации часто используют полиномы Чебышева. Полиномы Чебышева обеспечивают равноволновое приближение в полосе пропускания.Полиномы Чебышева первого рода в общем виде задаются соотношением
Tn(x)= cos (n arccos(x)) [3] (3.2)
Функция Tn(x) на отрезке [- 1 ; 1] изменяется в пределах от -1 до +1, переходя n раз через нуль и принимая 1 + n раз крайние значения (поочередно 1 или -1 ). При x>1 все полиномы T 1 + n(x) положительны, при x<-1 полиномы четных степеней положительны, нечетных — отрицательны. За пределами отрезка [ -1 ; 1] функция Tn(x) монотонно возрастает. Доказано, что из всех полиномов одинаковой степени, значение модуля которых на отрезке [-1 ; 1] не превышае тединицы, полином Чебышева за пределами этого отрезка принимает наибольшие по абсолютной величине значения. Данное свойство полиномов Чебышева обусловило их широкое применение при аппроксимации ХРЗ фильтров.[4]
3.1 АППРОКСИМАЦИЯ ПО ЧЕБЫШЕВУ ПРЯМАЯ (ПЕРВОГО РОДА)
Фильтр Чебышева — один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышева I рода)
Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.
Амплитудно-частотная характеристика фильтра чебышева 1-го порядка задаётся следующим образом:
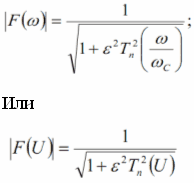
Здесь ωС — частота среза (для фильтра-прототипа она равна 1 рад/с), Тn(U) — полином Чебышева n-го порядка, n — порядок фильтра, ε — параметр, определяющий величину пульсаций АЧХ в полосе пропускания, ωС — частота среза, 
нормированная комплексная частота.
Полином Чебышева Тn(х) при х<1 колеблется в диапазоне -1... +1,
а при х >1 неограниченно возрастает по абсолютной величине. Поэтому АЧХ фильтра Чебышева первого рода в полосе пропускания (при |ω|<ωС) колеблется между значениями 
и 1, а вне полосы пропускания (при |ω|>ωС) монотонно затухает до нуля (см.рисунок 3.1.1)
Коэффициент передачи на нулевой частоте равен 1 при нечетном порядке фильтра, 
— при четном. На частоте среза коэффициент передачи фильтра равен 
, то есть уровню пульсаций АЧХ в полосе пропускания. При ω→∞ АЧХ стремится к нулю.[5]
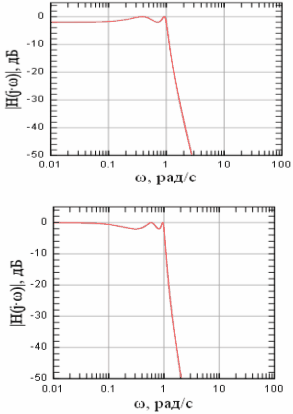
Рисунок 3.1 АЧХ фильтра Чебышева первого рода 4-го и 5-го порядков соответственно.
ФЧХ фильтра Чебышева изображены на рисунке 3.1.2.Из рисунка видно,что полоса пропускания становится более нелинейной при увеличении порядка фильтра. Обусловлено это колебательным видом АЧХ.[5]
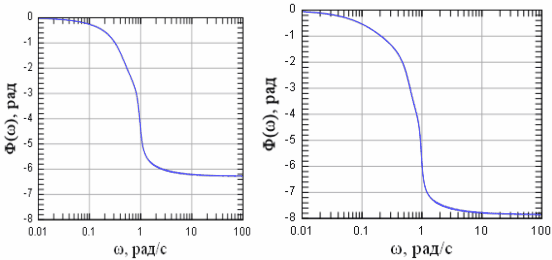
Рисунок 3.2 ФЧХ фильтра Чебышева первого рода 4-го и 5-го порядков соответственно
ХГВЗ фильтра Чебышева изображены на рисунке 3.1.3.В полосе пропускания при увеличении порядка фильтра отклоняется от идеальной функции . Это приводит к увеличению вклада фазовых искажений в общее искажение формы выходного сигнала.
Рисунок 3.3 ХГВЗ фильтра Чебышева первого рода 4-го и 5-го порядков соответственно
ХРЗ фильтра Чебышева на рисунке 3.1.4 имеет равноволновый характер в полосе пропускания и монотонный характер в переходной области и полосе задерживания. Количество колебаний в полосе пропускания возрастает с увеличением порядка фильтра.[5]
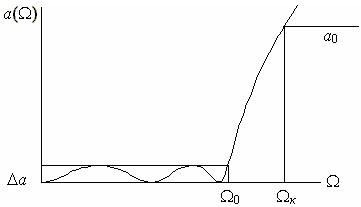
Рисунок 3.4 ХРЗ фильтра Чебышева
Временные характеристики фильтра Чебышева I рода (рисунок 3.1.5 )— импульсная переходная функция и переходная функция Импульсная переходная функция представляет собой реакцию фильтра на входной сигнал в виде дельта-функции Дирака, а переходная функция — реакцию на входное воздействие в виде единичной функции Хевисайда.
С увеличением порядка фильтра увеличиваются длительность переходного процесса, амплитуда колебаний (включая и амплитуду первого выброса), уменьшается размах основного лепестка импульсной характеристики при одновременном увеличении его длительности по уровню 0,5. Подобное поведение временных характеристик нежелательно при обработке импульсных сигналов, например телевизионных, поскольку при этом на изображении возникают окан-товки на яркостных переходах, уменьшается контрастность мелких деталей изображения.[5]
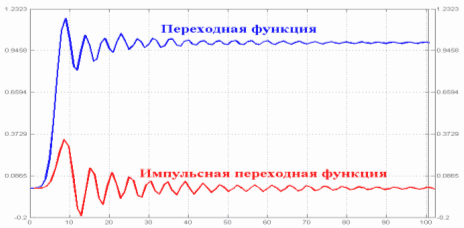
Рисунок 3.5 Импульсная переходная функция и переходная функция фильтра Чебышева
Похожие работы
... ; i3 – устройство основания; i4 – укладка дорожных плит; i5 – бурение; i5’ – вывоз изъятого грунта; i6 – монтаж арматуры; i7 – бетонирование; i8 – отрывка котлована под ростверк. До начала устройства буронабивных свай должны быть выполнены следующие работы: - разбиты и закреплены на местности оси опор и свай в свайном поле; - устроена площадка из железобетонных плит ПАГ по песчаному ...
... являются: а) Системы с изменением порядка следования комбинаций (РОС-ПП). В этих системах приемник стирает лишь комбинации, по которым решающим устройством РУ принято решение на стирание, и только по этим комбинациям посылает на передатчик сигналы переспроса. Остальные комбинации выдаются в ПИ по мере их поступления. Передатчик повторяет лишь комбинации, по которым приняты сигналы переспроса, ...
... порту в терминал. Рисунок 4.4. - Блок - схема передачи данных в терминал. Далее после окончания приема или передачи данных , в терминал передается команда "устройство свободно", что разрешает дальнейшие запросы на обмен данными. Перезагрузка программы в память и инициализация происходят при нажатии кнопки RESET. Полная блок-схема алгоритма предоставленна в приложении. Данный алгоритм ...
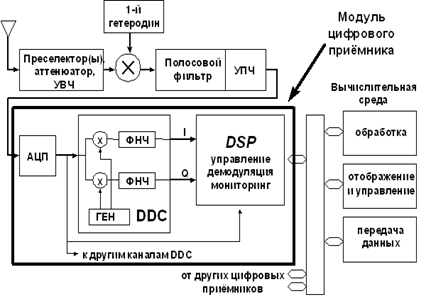
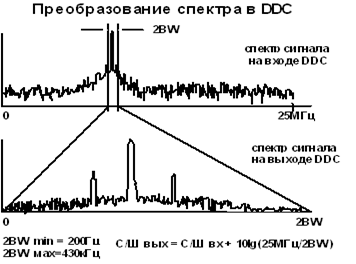
... схемы цифровых РПУ и сделаны выводы об их преимуществах, и применении в современной авиационной радиоэлектронной аппаратуре. 1.Обзор современных схем построения ЦРПУ 1.1 Схемы построения цифровых РПУ Обобщенная схема цифрового радиоприемного устройства представлена на рисунке 1. Рисунок 1 Развитие техники и технологии цифровых интегральных схем привело к тому, что заключительное ...
0 комментариев