АППРОКСИМАЦИЯ ЧЕБЫШЕВА ИНВЕРСНАЯ (ВТОРОГО РОДА)

3.2 АППРОКСИМАЦИЯ ЧЕБЫШЕВА ИНВЕРСНАЯ (ВТОРОГО РОДА)

При аппроксимации АЧХ многочленами Чебышева задавалась допустимая неравномерность АЧХ фильтров в полосе пропускания при помощи параметра εp . Однако можно также задать требуемый уровень подавления в полосе заграждения при помощи параметра , тогда получим фильтры Чебышева второго рода или как их еще называют инверсные фильтры Чебышева. Аппроксимирующая функция в этом случае задается выражением , а квадрат модуля АЧХ представляется в виде:

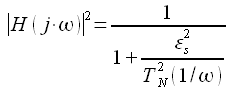 (3.5)

На рисунках показаны аппроксимирующая функция  и квадрат модуля АЧХ фильтра Чебышева второго рода порядка N=4 при  (уровень подавления в полосе заграждения равен )

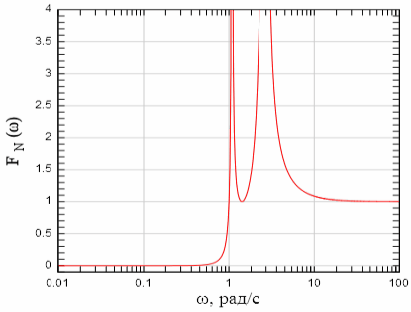
Рисунок 3.3: Аппроксимирующая функция фильтра Чебышева второго рода 4-го порядка

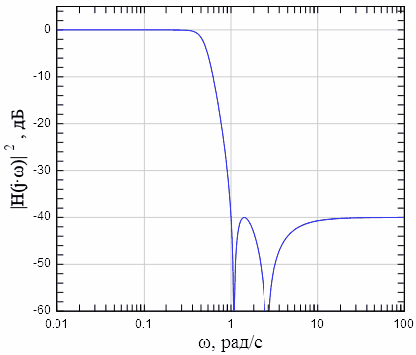
Рисунок 3.4: Квадрат модуля АЧХ фильтра Чебышева второго рода 4-го порядка

Если нормированный фильтр Чебышева первого рода на частоте  «пропускает» сигнал, т.к.  Близко к единице (0 дБ), то нормированный фильтр Чебышева второго рода на частоте  «подавляет» сигнал, т.к. .[4]

Фильтры Чебышева второго рода целесообразно использовать для полосозаграждающих фильтров с заданным коэффициентом подавления.[4]

4. ВЫВОД ПЕРЕДАТОЧНОЙ ФУНКЦИИ ФИЛЬТРА ПО СТРУКТУРЕ РАУХА

В варианте данной курсовой работы предложено спроектировать полосовой фильтр восьмого порядка, используя структуру Рауха.

С целью вывода передаточной функции полосового фильтра по структуре Рауха рассмотрим фильтры второго порядка, которые будут соединены каскадно:

	К1(р)		К2(р)		К3(р)		К4(р)

Рис.4.1 Структурная схема фильтра восьмого порядка

Построим принципиальную схему полосового фильтра восьмого порядка на операционном усилителе. Полосовой фильтр пропускает составляющие сигнала с частотами, лежащими между левой и правой частотой среза, а остальные задерживает, исходя из этого присутствие разделительных конденсаторов в ветвях схемы необходимо. Чтобы определить в какой именно ветви они должны стоять, сначала во все ветви поставим проводимости.

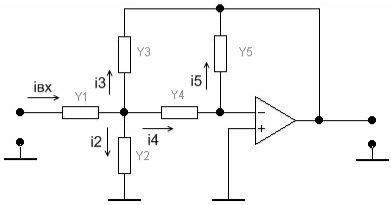
Рис.4.2 – Функциональная схема структуры Рауха второго порядка.

Найдём передаточную функцию каждого каскада.

 (4.1)

Применим законы Кирхгофа:

 (4.2)

 (4.3)

 (4.4)

 (4.5)

 (4.6)

(4.7)

(4.8)

 (4.9)

Ток i4 протекает через проводимость Y4 и втекает в ветвь с проводимостью Y5 без потерь. Подставим (4.7), (4.8), (4.6) в (4.2), а затем получившееся выражение подставим в (4.5):

(4.10)

Подставим (4.4) в (4.10) и преобразуем, чтобы получить окончательное выражение для передаточной функции:

(4.11)

(4.12)

Общая же формула передаточной характеристики полосового фильтра имеет вид:

 (4.13)

 

Анализируя выражения передаточной характеристики фильтра, определим типы проводимостей для обеспечения требуемой степени p. Так, сделаем вывод о том, что проводимости Y1, Y2 и Y5 должны заменить резисторы, а проводимости Y3 и Y4 – емкости:

     (4.14)

Подставив (4.14) в (4.12) и преобразовав к виду (4.13), получим:

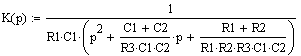 (4.15)

Таким образом, коэффициенты нормированного ФНЧ-прототипа для одного звена второго порядка можно представить следующим образом:

С учётом (4.14) построим принципиальную схему фильтра.

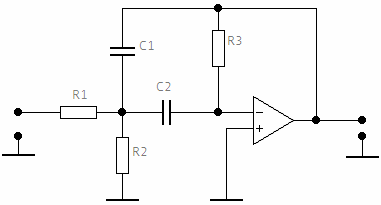
Рис.4.3 – Функциональная схема структуры Рауха второго порядка.

Данное функциональное звено представляет собой активный фильтр второго порядка, построенный на основе операционного усилителя.

5 МОДЕЛИРОВАНИЕ ФИЛЬТРА НА ФУНКЦИОНАЛЬНОМ УРОВНЕ В СИСТЕМЕ MATHCAD В ЧАСТОТНОЙ И ВРЕМЕННОЙ ОБЛАСТЯХ (РАСЧЕТ АЧХ, ФЧХ, ХРЗ, ХГВЗ, ИХ, ПХ В НОРМИРОВАННОМ И ДЕНОРМИРОВАННОМ ВИДАХ)

Для моделирования на функциональном уровне будем использовать Math CAD .

Операторную передаточную функцию можно записать в следующем виде:

(5.1)

где K(w)-амплитудно-частотная характеристика;

φ(w)-фазо-частотная характеристика.

Амплитудно-частотная характеристика определяется следующим образом:

(5.2)

Фазо-частотная характеристика определяется следующим образом:

(5.3)

Построим АЧХ и ФЧХ в Math CAD:

Исходные данные:

  

Построим АЧХ фильтра прототипа нижних частот:

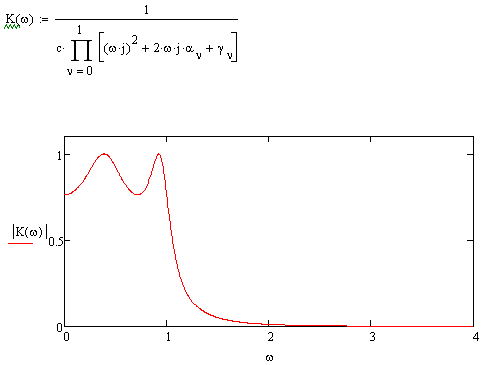
Рисунок 5.1 АЧХ фильтра прототипа нижних частот в нормированном виде

Для построения характеристик ПФ, осуществим пересчёт параметров.

Исходя из того, что

Kфнч(p)=А(p~+1/p~)=Kпф(p~) (5.4)

Получим выражения для пересчёта параметров:

 

В выражениях 5.5-5.13 , где  и .

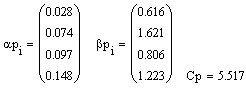
Построим АЧХ ПФ.

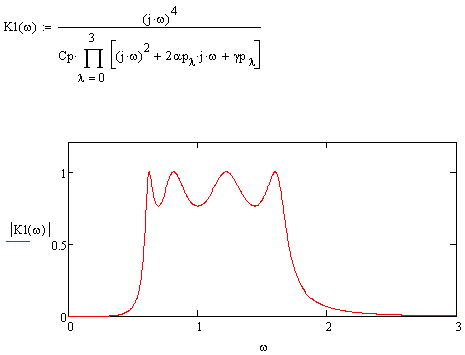
Рисунок 5.2 АЧХ ПФ в нормированном виде

Построим ФЧХ ПФ.

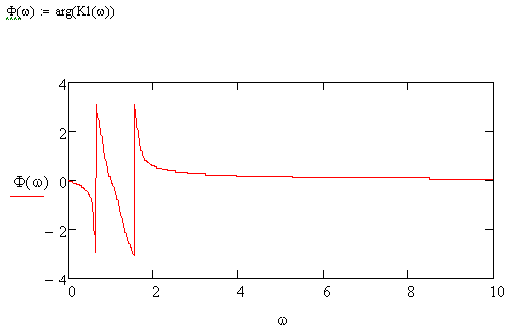
Рисунок 5.3 ФЧХ ПФ в нормированном виде

Построим характеристику рабочего затухания.

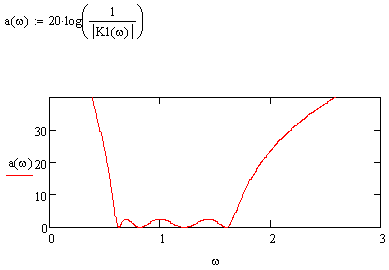
Рисунок 5.4 ХРЗ ПФ в нормированном виде

Построим характеристику группового времени запаздывания:

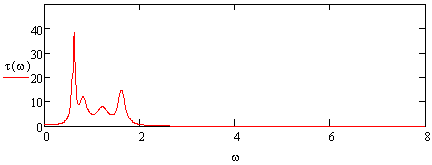
Рисунок 5.5 ХГВЗ ПФ в нормированном виде

Построим импульсную и переходную характеристики:

Так как импульсная характеристика – это реакция системы на δ-функцию, выражение для её построения получим следующим образом:

Uвх=δ(t) 1

Uвых=K(p)* Uвх(p)

 

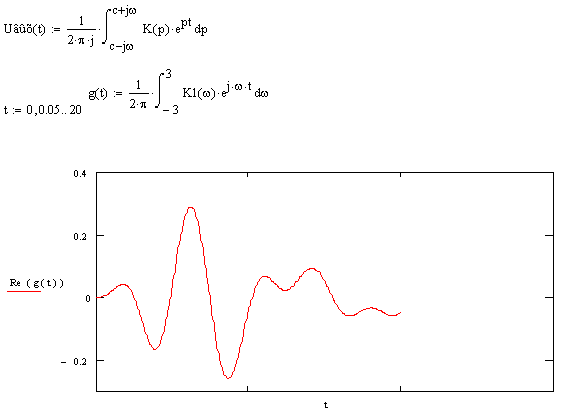
Рисунок 5.6 ИХ ПФ в нормированном виде

Переходная характеристика – реакция системы на единичный скачок(на функцию Хевисайда), поэтому выражение для её построения получим следующим образом:

1(t) 1/p

h(t)= Uвых(t)=1/2*П*j

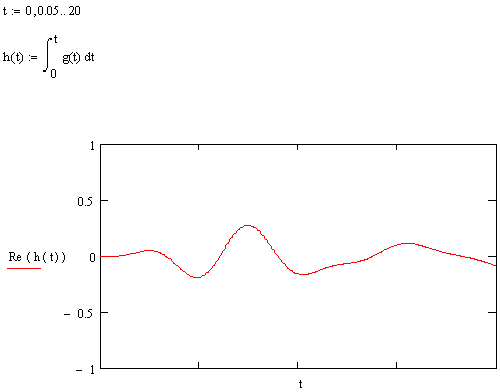
Рисунок 5.7 ПХ ПФ в нормированном виде

Чтобы построить данные характеристики фильтра в денормированном виде, необходимо получить параметры ПФ в денормированном виде. Для этого воспользуемся следующими выражениями:

 (5.14)

(5.15)

 (5.16)

 (5.17)

В этих выражениях  - денормированная частота, а  .

Таким образом деномированные коэффициенты равны:

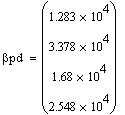  Сpd=2.925739792537995685239e-17

Построим АЧХ ПФ в денормированном виде:

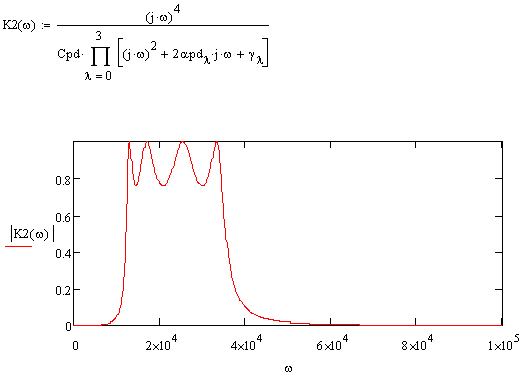
Рисунок 5.8 АЧХ ПФ в денормированном виде

Построим фЧХ ПФ в денормированном виде:

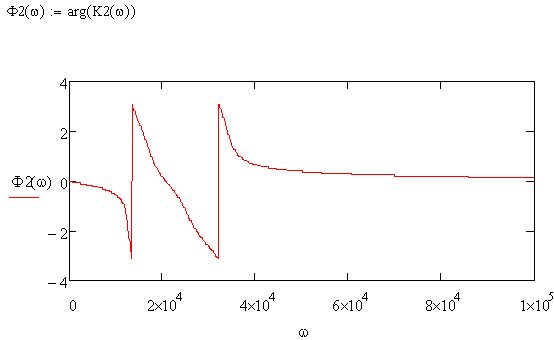
Рисунок 5.9 ФЧХ ПФ в денормированном виде

Построим ХРЗ ПФ в денормированном виде:

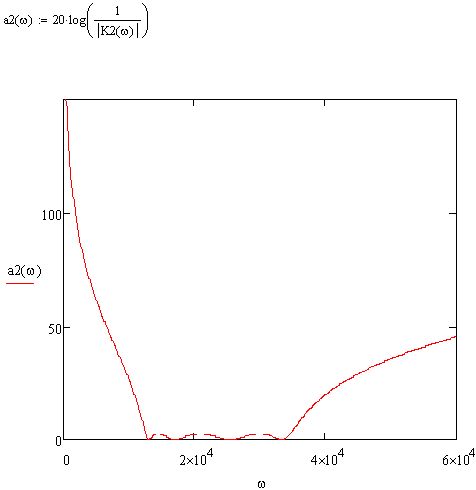
Рисунок 5.10 ХРЗ ПФ в денормированном виде

Построим ХГВЗ ПФ в денормированном виде:

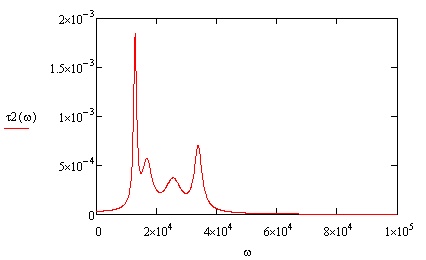
Рисунок 5.11 ХГВЗ ПФ в денормированном виде

Построим ИХ и ПХ ПФ в денормированном виде:

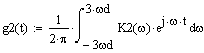
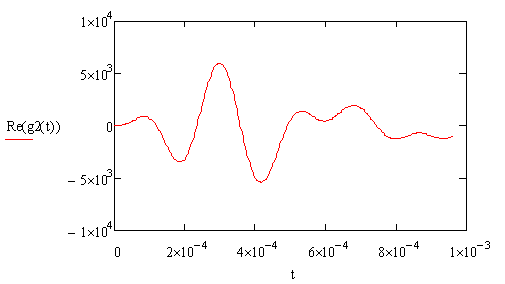
Рисунок 5.12 ИХ ПФ в денормированном виде

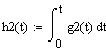
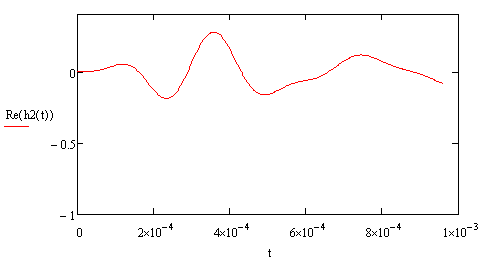
Рисунок 5.13 ПХ ПФ в денормированном виде

Анализ результатов вычислений показывает, что операция денормирования произведена верно, так как характеристики фильтра в денормированном виде отличны от характеристик в нормированном виде представляемой областью частот.