Дослідження методу ортогоналізації й методу сполучених градієнтів

Курсова робота

На тему:

"Дослідження методу ортогоналізації й методу сполучених градієнтів"

Введення

До рішення систем лінійних алгебраїчних рівнянь приводяться багато задач чисельного аналізу.

Відоме з курсу вищої алгебри правило Крамера для рішення систем лінійних алгебраїчних рівнянь практично невигідно, тому що вимагає занадто великої кількості арифметичних операцій і записів. Тому було запропоновано багато різних способів, більше придатних для практики.

Використовувані практично методи рішення систем лінійних алгебраїчних рівнянь можна розділити на дві більші групи: так звані точні методи й методи послідовних наближень. Точні методи характеризуються тим, що з їхньою допомогою принципово можливо, проробивши кінцеве число операцій, одержати точні значення невідомих. При цьому, звичайно, передбачається, що коефіцієнти й праві частини системи відомі точно, а всі обчислення виробляються без округлень. Найчастіше вони здійснюються у два етапи. На першому етапі перетворять систему до того або іншого простого виду. На другому етапі вирішують спрощену систему й одержують значення невідомих.

Методи послідовних наближень характеризуються тим, що із самого початку задаються якимись наближеними значеннями невідомих. Із цих наближених значень тим або іншому способу одержують нові «поліпшені» наближені значення. З новими наближеними значеннями надходять точно також і т.д. Розглянемо два точних методи: метод ортогоналізації й метод сполучених градієнтів.

1.  Метод ортогоналізації

1.1 Метод ортогоналізації у випадку симетричної матриці

Нехай дана система

 (1)

порядку n. Щоб уникнути надалі плутанини, над векторами поставимо риски. Рішення системи будемо розшукувати у вигляді

, (2)

де  – n векторів, що задовольняють умовам

 при  (3)

Тут розглядається звичайний скалярний добуток векторів в n-мірному векторному просторі, тобто якщо  й , те . Нехай такі вектори знайдені. Як це робиться, буде показано нижче. Розглянемо скалярний добуток обох частин системи (1) з

 (4)

Використовуючи (2) одержимо:

 (5)

або, у силу вибору векторів ,

. (6)

Отже, для визначення коефіцієнтів  одержали систему із трикутною матрицею. Визначник цієї системи дорівнює

 

. (7)

Отже, якщо , те  можливо знайти й перебувають вони без праці.

Особливо легко визначаться , якщо матриця А симетрична. У цьому випадку, мабуть,

 (8)

і, отже,

=0 при . (9)

Тоді система для визначення  прийме вид

 (10)

. (11)

Метод можна узагальнити. Нехай якимсь образом удалося знайти систему 2n векторів  так, що

 =0 при . (12)

Множачи обидві частини рівності (1) на  й використовуючи подання  через , як і раніше, одержимо:

. (13)

Знову вийшла система лінійних алгебраїчних рівнянь із трикутною матрицею для визначення . Трохи ускладнивши обчислення можна одержати систему діагонального виду. Для цього побудуємо три системи векторів , так що мають місце рівності:

 (14)

 (15)

 (16)

Тоді

, (17)

тому що при i<r

 (18)

і при i>r

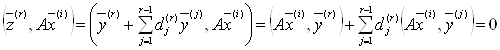 (19)

Таким чином,

 (20)

Зупинимося докладніше на першому з описаних методів. Розглянемо випадок, коли матриця А симетрична й позитивно певна. Останнє означає, що для будь-якого вектора  квадратична форма його компонент  більше або дорівнює нулю, причому рівність нулю можливо в тім і тільки тім випадку, якщо вектор  нульової. Як ми бачили раніше, потрібно побудувати систему векторів , що задовольняють умовам

 =0 . (21)

Це побудова можна здійснити в такий спосіб. Виходимо з якоїсь системи лінійно незалежних векторів , наприклад із системи одиничних векторів, спрямованих по координатних осях:

 (22)

Далі проводимо «ортогоналізацію». Приймаємо  й шукаємо  у вигляді

. (23)

З умови  знаходимо:

 (24)

Шукаємо  у вигляді

. (25)

Умови  спричиняють

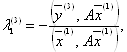
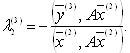  (26)

Далі надходимо також.

Процес буде здійсненний, тому що все . Це ж забезпечить нам можливість розв'язання системи для визначення коефіцієнтів . Помітимо, що в нашім випадку це буде процес справжньої ортогоналізації, якщо в просторі векторів увести новий скалярний добуток за допомогою співвідношення

. (26)

Неважко перевірити, що уведене таким способом скалярний добуток буде задовольняти всім вимогам, які до нього пред'являються.

При рішенні системи n рівнянь за справжньою схемою потрібно зробити

 (28)

операцій множення й ділення.