Метод ортогоналізації у випадку несиметричної матриці

1.2  Метод ортогоналізації у випадку несиметричної матриці

У випадку несиметричної матриці процес ортогоналізації проводиться точно також. Нехай вектори  вже побудовані. Тоді  шукається у вигляді

 (29)

Коефіцієнти  визначаються із системи

 (30)

Система у випадку несиметричної матриці буде трикутною.

Аналогічно будується система «біортогональних» векторів, тобто система 2n векторів, що задовольняють умові (12). При цьому  – n довільних лінійно незалежних векторів, а вектори  будуються послідовно у вигляді

 (31)

Коефіцієнти  перебувають із системи

 (32)

Також надходимо, відшукуючи коефіцієнти  й , при побудові систем векторів (14) і (15), що задовольняють умовам (16).

При цьому одержимо дві системи:

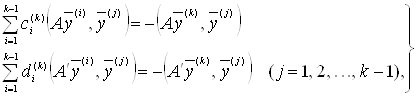 (33)

з яких і визначаємо  й .

Зупинимося ще на одному методі ортогоналізації. Будемо розглядати рядки матриці А як вектори:

 (34)

Перше рівняння системи  ділимо на 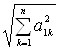. При цьому одержимо

 (35)

де

 (36)

Друге рівняння системи заміниться на

 (37)

де

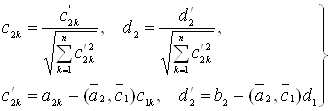 (38)

Аналогічно надходимо далі. Рівняння з номером i прийме вид

 (39)

де

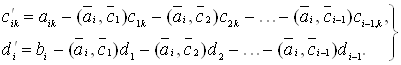 (40)

Процес буде здійсненний, якщо система рівнянь лінійно незалежна. У результаті ми прийдемо до нової системи , де матриця З буде ортогональної, тобто має властивість СС¢=I.

Таким чином, рішення системи можна записати у вигляді

. (41)

Практично, внаслідок помилок округлення, СС¢ буде відмінна від одиничної матриці й може виявитися доцільним зробити кілька ітерацій для системи .

2.  Метод сполучених градієнтів

2.1 Перший алгоритм методу

Нехай потрібно вирішити систему лінійних алгебраїчних рівнянь

(1)

с позитивно певною матрицею A порядку n.

Розглянемо функціонала

, (2)

багаточлен, що представляє, другого порядку відносно _x1, _x2…, x_n,… Позначимо через  рішення системи (1), тобто . У силу симетричності й позитивної визначеності матриці, маємо:

При цьому знак рівності можливий лише при . Таким чином, задача рішення рівняння (1) зводиться до задачі відшукання вектора , що обертає в мінімум функціонал (2).

Для відшукання такого вектора застосуємо наступний метод.

Нехай  – довільний початковий вектор, а

 (4)

– вектор не в'язань системи. Покажемо, що вектор не в'язань  має напрямок нормалі до поверхні в крапці . Справді, напрямок нормалі збігається з напрямком найшвидшої зміни функції  в крапці . Це напрямок ми знайдемо, якщо знайдемо серед векторів , для яких , такий вектор, що

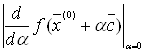
має найбільше значення. Але

Але серед векторів  постійний довжини  досягає максимального значення, якщо  має напрямок вектора  або йому протилежне. Твердження доведене. Будемо рухатися із крапки  в напрямку вектора  доти, поки функція  досягає мінімального значення. Це буде при , тобто при

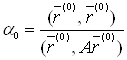. (5)

Вектор

 (6)

і приймаємо за нове наближення до рішення.

У методі сполучених градієнтів наступне наближення  перебуває так. Через крапку  проведемо гіперплощину (n-1) – го виміру

 (7)

і через  позначимо нове не в'язання системи

. (8)

Вектор  спрямований по нормалі до поверхні  в крапці , а вектор  паралельний дотичної площини в цій крапці. Тому

. (9)

Гіперплощина (7) проходить через крапку , тому що

.

При кожному  вектор  паралельний деякої нормальної площини до поверхні  в крапці . Знайдемо серед них той, котрий лежить у гіперплощині (7), тобто ортогональний к. З умови ортогональності маємо:

,

або

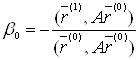. (10)

Вектор

 (11)

має напрямок нормалі до перетину поверхні  гіперплощини (7) у крапці . Будемо рухатися із крапки  в напрямку вектора  доти, поки функція  досягне мінімуму. Це буде при

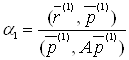. (12)

Вектор

приймемо за нове наближення до рішення  системи. Вектор не в'язань

 (13)

має напрямок нормалі до поверхні  в крапці . Покажемо, що він буде ортогональний до  і . Справді, використовуючи (9), (11), (12), (13), маємо:

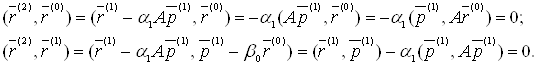
Розглянемо гіперплощину (n-2) – х вимірів

, (14)

минаючу через крапку . Ця гіперплощина містить і , тому що ми раніше бачили, що , а

.

Вектор  при кожному  паралельний гіперплощини (7), тому що

.

Підберемо  так, щоб він був паралельний і гіперплощини (14), тобто зажадаємо ортогональності до вектора . Будемо мати:

,

або

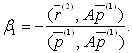 (15)

Вектор

 (16)

буде мати напрямок нормалі до перетину поверхні гіперплощиною (14) у крапці . Із крапки  змістимося в напрямку цього вектора так, щоб функція  досягла мінімального значення. Це буде при

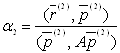, (17)

 (18)

приймемо за нове наближення к. Новий вектор не в'язань буде:

. (19)

Продовжуючи процес, одержимо послідовності векторів , , , обумовлені рекурентними співвідношеннями:

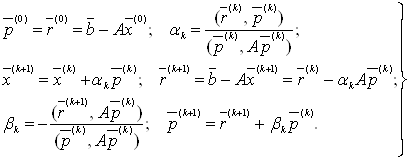 (20)

Для цих векторів мають місце наступні співвідношення:

 (21)

 (22)

Справді, у силу самої побудови при i (j

Далі, при i>j

Якщо i=j+1, то права частина дорівнює нулю, у силу визначення , якщо ж i>j+1, те, по доведеному, і

.

Продовжуючи зниження індексу у вектора , через кілька кроків прийдемо до скалярного добутку  (по визначенню ). Таким чином, співвідношення (21) доведені. Для доказу (22), у силу рівноправності індексів i і j, припустимо, що i>j. Тоді

.

Тому що в n-мірному векторному простори не може бути більше n взаємно ортогональних векторів, то на деякому кроці  одержимо , тобто  буде рішенням системи (1).

На мал. 1 показана геометрична картина нашої побудови при n=3.

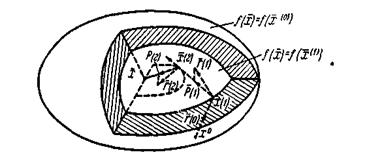
Мал. 1