Проектирование управляемого привода в электромеханических системах

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: "Проектирование управляемого привода в электромеханических системах"

Техническое задание на проектирование управляемого электропривода

1. Конструктивная схема (рис. 1) промышленного робота (ПР) с грузоподъемностью от 10 до 30 кг, используемого в сборочных операциях в автомобильной промышленности. ПР – автоматическая стационарная машина, имеющая исполнительный механизм (манипулятор) с тремя степенями подвижности. Два механизма поворота, расположенные в шарнирах 1 и 2, осуществляют программные повороты j₁(t), j₂(t) вокруг вертикальных осей (1–1 и 2–2 соответственно), механизм подъема 3 осуществляет поступательное перемещение С₃(t) объекта манипулирования, зажатого в захватывающем механизме 4. В механизме подъема 3 использована зубчато-реечная передача с зубчатой рейкой 5 и зубчатой шестерней 6.

 

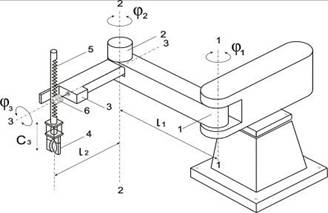
Рис. 1. Конструктивная схема промышленного робота

2. Перемещения по степеням подвижности осуществляются последовательно, начиная с перемещения j₁(t).

3. Силовой модуль первого из индивидуальных приводов промышленного робота (рисунок 1) сосредоточен в центре масс шарнира 1. Центр тяжести груза (объекта манипулирования) совпадает с центром приведения масс захватывающего механизма 4.

4. Для данного ТЗ управляемый привод по координате j₁(t) – программный, типа «угол – угол».

5. Описание и параметры программных траекторий рабочих циклов исследуемого привода приведены на рисунках 2 и 3.

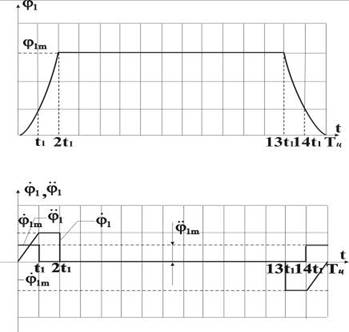
Рис. 2. Первая из двух возможных траекторий рабочего цикла для первого привода

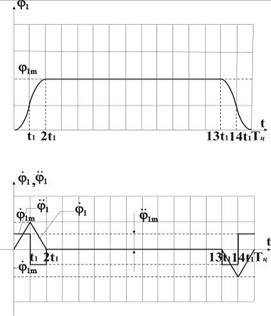
Рис. 3. Вторая из двух возможных траекторий рабочего цикла для первого привода

6. Масса зубчатой рейки m_p = 5 кг, минимальное m_min = 15,5 кг и максимальное m_max= 25 кгзначения массы груза вместе с массой захватывающего механизма.

7. Длина звеньев манипулятора l₁= 0,5 ми l₂= 0,5 м(рис. 1).

8. Массы звеньев m₁= 54 кг и m₂ = 4 кг.

9. Расстояние от центров масс звеньев до соответствующих шарниров

r₁ = 0,25 м иr₂ = 0,25 м.

10. Динамические моменты инерции J₁ = 0,3 кг^.м² и J₂= 0,25 кг^.м²первого и второго звеньев относительно вертикальных осей, проходящих через их центры масс. Максимальный J_3max = 0,3 кг^.м²и минимальный J_3min= 0,15 кг^.м² динамические моменты инерции третьего звена: зубчатой рейки с захватывающим механизмом и грузом.

11. Коэффициент вязкого трения К_вт = 0,04.

12. Момент сухого трения М_о = 0,05 Н^.м.

13. КПД редуктора h = 0,65.

14. Передаточное отношение зубчато-реечной передачи i_рп.

15. Параметры усилителя мощности k_у = 220, T_m = 0,0015 с.

16. Статическая e_cт = 1,0% и динамическая e_д = 0,9% допустимые погрешности привода.

17. Прямые показатели качества: перерегулирование s = 25% и время переходного процесса t_пп = 1,5 c.

Введение

Управляемый электропривод получил широкое применение во всех сферах жизни и деятельности общества от промышленного производства до бытовой техники. Широта применения определяет исключительно большой диапазон мощностей электроприводов и значительное разнообразие их исполнения. В управляемом электроприводе нашли применение и получили развитие основные достижения современной техники управления.

В ходе выполнения курсовой работы необходимо разработать конкретный электропривод, программно управляющий угловым перемещением промышленного робота-манипулятора по одной из трех степеней подвижности.

Для наглядности корректности функционирования синтезированного управляемого электропривода выполнение работы включает построение его цифровой модели и оценку ее качественных показателей, используя средства компьютерного моделирования.

1 Энергетический расчет привода   1.1 Определение заданных программных траекторий

Определим постоянную времени , относительно которой рассчитываются уравнения траекторий

, (1.1)

.

Приведем максимально возможное значение угловой координаты перемещаемой нагрузки к размерности [рад].

,  (1.2)

Рассчитаем неопределенные параметры для первой возможной траектории движения рабочей нагрузки за время одного цикла работы двигателя.

Таблица 1.1

t
[0; t1]		at	a
[t1; 2t1]		b	0
[2t1; 13t1]		0	0
[13t1; 14t1]			0
[14t1; Tц]			a

Для нахождения параметров траектории решим систему уравнений (1.3), приравняв значения угла поворота и скорости нагрузки в общих для сопряженных участках точках.

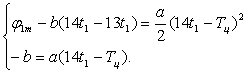. (1.3)

Из второго уравнения системы (1.3) получим зависимость для параметра b и подставим его в первое выражение.

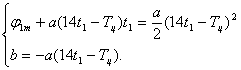. (1.4)

Получим численные значения параметров a и b.

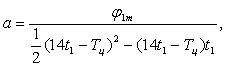 (1.5)

По формуле 1.5 найдем параметры a и b:

 

.

Таблица 1.2

	, рад	, рад.c-1	, рад.c-2
[0; 1.333]			0.916
[1.333; 2.667]		1.2215	0
[2.667; 17.333]		0	0
[17.333; 18.667]		-1.2215	0
[18.667; 20]			0.916

Максимальные значения:

а) угла поворота нагрузки _1m(t) = 2.443 рад,

б) угловой скорости нагрузки p_1m(t) = 1.2215 рад/c^-1,

в) углового ускорения нагрузки p²_1m(t) = 0.916 рад/c^-2.

Рассчитаем неопределенные параметры для второй возможной траектории движения рабочей нагрузки за время одного цикла работы двигателя.

Таблица 1.3

t, c
[0; t1]		at	a
[t1; 2t1]
[2t1; 13t1]		0	0
[13t1; 14t1]
[14t1; Tц]			a

Для нахождения параметров траектории решим систему уравнений (1.6), приравняв значения угла поворота и скорости нагрузки в общих для сопряженных участках точках.

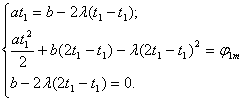, (1.7)

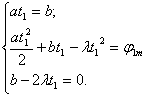. (1.8)

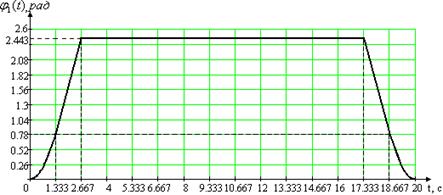
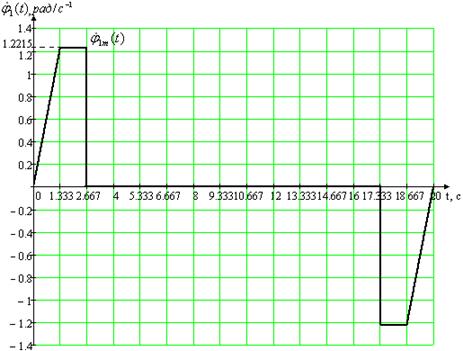
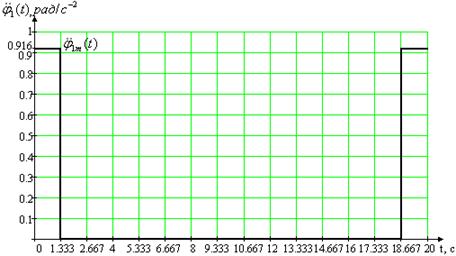
Рис. 1.1. Первая из двух возможных траекторий рабочего цикла для первого привода

Из первого уравнения системы (1.8) получим формулу для параметра b и подставим его в третье выражение, а затем функциональные зависимости для параметров a и b – во второе уравнение

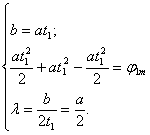, (1.10)

Получим численные значения параметров a, b и :

,

,

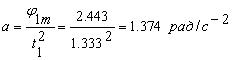Таблица 1.4

t, c
[0; 1.333]		1.374t	1.374
[1.333; 2.667]
[2.667; 17.333]		0	0
[17.333; 18.667]
[18.667; 20]			1.374

Максимальные значения:

а) угла поворота нагрузки _1m(t) = 2.443 рад,

б) угловой скорости нагрузки p_1m(t) = 1.833 рад/c^-1,

в) углового ускорения нагрузки p²_1m(t) = 1.374 рад/c^-2.

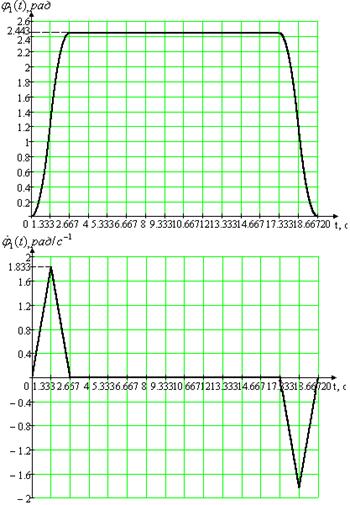
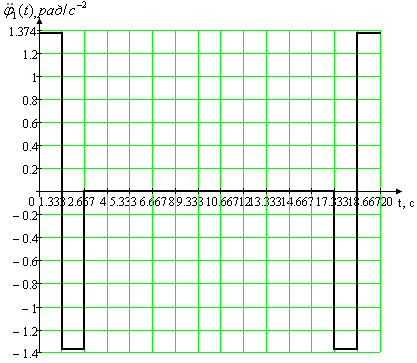
Рис. 1.2. Вторая из двух возможных траекторий рабочего цикла для первого привода

1.2 Расчет статической и динамической нагрузки на проектируемый привод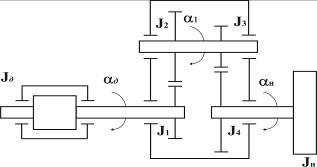

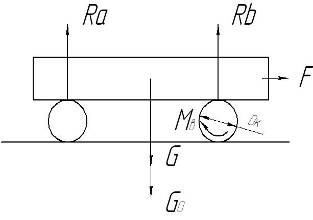
Рис. 1.3. Многомассовая нагрузка привода

При определении энергетических параметров проектируемого привода сложную многомассовую нагрузку привода (рис. 1.3) приводят к одному валу – валу двигателя. Для этого многомассовую нагрузку с мощностью  заменяют маховиком той же мощности на валу двигателя  и вращающимся со скоростью вала двигателя.

, (1.11)

где  – к.п.д. механической передачи от вала нагрузки к валу двигателя.

С другой стороны,

 

, (1.12)

где  – момент приведенной нагрузки к валу двигателя,  – момент на валу нагрузки, ,  – угловые скорости вала двигателя и вала нагрузки, соответственно (рис. 1.3), . Подставляя (1.12) в (1.11), получаем:

 

,

откуда:

 

,

где – передаточное отношение механической передачи между валом двигателя и валом нагрузки (передаточное число редуктора).

Моменты, действующие на валу нагрузки, можно разделить на две группы. К первой группе относятся динамические моменты , величина которых пропорциональна ускорениям и моментам инерции движущихся масс нагрузки. Ко второй группе относятся моменты статические , связанные с противодействующими усилиями: моменты сухого и вязкого трения, момент статического сопротивления подъему груза.

Таким образом, момент нагрузки, приведенный к валу двигателя,

. (1.13)

Динамические моменты нагрузки приводов

Динамический момент нагрузки первого привода определяется уравнением

 

, (1.14)

где – ускорение на валу нагрузки; – момент инерции нагрузки.

Нагрузка первого привода является телом сложной конфигурации, поэтому  определим как сумму моментов инерции отдельных частей нагрузки относительно оси вращения 1–1:

 

 (1.15)

Динамический момент инерции третьего звено J₃ принимает значения в диапазоне от J_{3 min} до J_{3 max.} Масса груза, зажатого в захватном устройстве m, может меняться в пределах от m_min до m_max. Изменение данных параметров приводит к изменению момента инерции нагрузки J_.

Определим минимальное и максимальное значение момента инерции нагрузки J_:

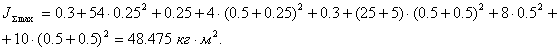
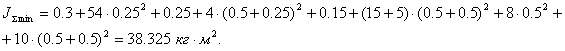
Наибольшего значения величина динамического момента нагрузки привода достигает при максимальном угловом ускорении рабочей нагрузки

 

(1.16)

Определим максимальный динамический момент нагрузки привода для первой возможной траектории рабочего цикла первого привода по формуле 1.16.

Определим максимальный динамический момент нагрузки привода для второй возможной траектории рабочего цикла первого привода:

Статические моменты нагрузки приводов

Движению в механизмах поворота противодействуют статические моменты сопротивления: моменты вязкого и сухого трения, характерные для зубчатых передач механизмов поворота.

Момент вязкого трения пропорционален угловой скорости вала нагрузки и определяется уравнением:

 

(1.17)

где  – коэффициент вязкого трения, зависящий от вязкости и температуры смазывающих масел.

Момент сухого трения в большинстве случаев считают независимым от скорости и направленным против нее:

 

 (1.18)

здесь .

Согласно (1.17), (1.18), статический момент нагрузки первого привода

 

 (1.19)

а его максимальное значение

 

 (1.20)

По формуле 1.20 найдем максимальный статический момент нагрузки привода для первой возможной траектории рабочего цикла:

.

По формуле 1.20 найдем максимальный статический момент нагрузки привода для второй возможной траектории рабочего цикла:

.

1.3 Предварительный выбор двигателя

Исходными данными для выбора двигателя являются приведенный к валу двигателя момент рабочей нагрузки , максимальные значения скорости и ускорения нагрузки, определяемые по возможным траекториям рабочего цикла.

Выбор исполнительного двигателя начнем с расчета требуемой максимальной мощности  на валу двигателя в рабочем режиме. При этом предположим, что нагрузка перемещается с максимально возможными скоростью и ускорением. Мощность двигателя должна быть достаточной для обеспечения этого режима, наиболее тяжелого для двигателя.

Для первого привода, осуществляющего поворот , требуемая мощность  исполнительного двигателя, с учетом (1.14) и (1.19):

 

.  (1.21)

По формуле 1.21 вычислим требуемую мощность двигателя для отработки первой из двух возможных траекторий движения рабочей нагрузки:

.

По формуле 1.21 вычислим требуемую мощность двигателя для отработки второй из двух возможных траекторий движения рабочей нагрузки

.

Выберем исполнительный двигатель с номинальной мощностью не меньшей .

Выбор будем осуществлять согласно следующим критериям:

1.  – привод ПР работает в интенсивных динамических режимах требующих высокого быстродействия, поэтому необходимо выбирать двигатель с минимальным собственным моментом инерции,

2.  – при уменьшении массы двигателя – уменьшается статические и динамические нагрузки на 1 и 2 приводы в ПР,

3.  – т. к. увеличивается качество регулирования,

4.  – поскольку уменьшение сопротивления в якорной цепи приводит к снижению нагрева двигателя,

5.  – чем ниже скорость вращения двигателя, тем меньшее передаточное число требуется обеспечить, а, следовательно, выбрать более простой редуктор, подходящий по массогабаритным характеристикам и его КПД,

6.  – больший ток в якорной цепи обеспечивает выше номинальный момент двигателя (мощность).

 (1.22)

Согласно (1.22), для первой траектории будем выбирать двигатель, придерживаясь данных значений мощности: .

Для обеспечения движения рабочей нагрузки по первой из двух рассматриваемых траекторий наиболее подходящими приводами являются двигатели [1], приведенные в таблице 1.5.

Таблица 1.5

Серия двигателя	Тип двигателя	Pдном, Вт	nдном, рад/с	Uя ном, В	Iяном, А	Rя, Ом	Jд.10-6 кг∙м2	Tяц, мс	mд, кг
ДВИ	ДВИ-211–02	120	628	27	7.4	1.3	23	0.50	3.4
СД	СД-150	150	786	60	4.2	2.8	193	0.3	2.7

Для второй траектории, .

Для обеспечения движения рабочей нагрузки по второй траектории наиболее подходящими приводами являются двигатели [1], приведенные в таблице 1.6.

Таблица 1.6

Серия двигателя	Тип двигателя	Pдном Вт	рад/с	Uя ном, В	Iяном, А	Rя, Ом	Jд, кг∙м2	Tяц, мс	mд, кг
2П	2ПБ90МУХЛ4	280	167.6	110	3.9	2.69	0.004	23.05	24
ДВИ	ДВИ-321–02	340	111	110	4.0	2.85	0.005	22.63	27

1.4 Выбор передаточного числа редуктора

Для определения передаточного числа редуктора привода используется графический метод, позволяющий просто учесть нежесткость механической характеристики двигателя.

. (1.23)

По уравнению требуемого момента на валу двигателя (1.23) строится график зависимости максимального значения момента  от передаточного числа редуктора i. На график наносят прямую, параллельную оси абсцисс, ограничивающую значения момента, допустимого на валу двигателя с учетом возможной перегрузки его по мощности:

, (1.24)

где  – номинальный момент выбранного двигателя.

Минимальное значение требуемого  достигается при передаточном отношении редуктора , которое обращает в ноль производную .

Если , то возможных значений  не существует, следует выбрать другой двигатель и повторить расчеты.

Выбранный диапазон возможных значений i корректируют, исходя из условия обеспечения требуемого максимального значения угловой скорости нагрузки :

 

 (1.25)

где – располагаемая скорость двигателя при максимальном требуемом моменте на его валу.

На другом графике строят механическую характеристику двигателя по уравнениям:

, (1.26)

где ,

.

Индексом _ном обозначены номинальные параметры выбранного двигателя.

 – коэффициент потерь, вводимый для обеспечения запаса по скорости, рекомендуется выбирать .

Теперь найдем передаточное число редуктора для каждого выбранного двигателя.

  1.4.1 Первый двигатель для первой траектории

Зависимость  имеет вид:

, (1.27)

Подставим данные двигателя сети ДВИ (таблица 1.5) в уравнение момента (1.27), получим зависимость максимального значения момента  от передаточного числа редуктора i:

,

.

Найдем значение номинального момента  по формуле:

. (1.28)

.

Используя (1.24) найдем :

.

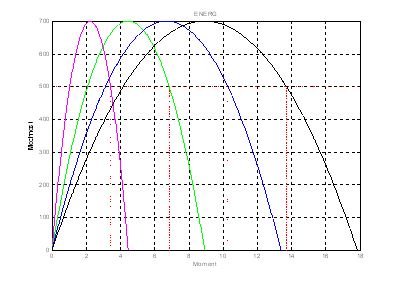
При помощи программного пакета MathCad построим графики зависимости максимального момента (рис. 1.4), а также по формуле 1.26 механическую характеристику (рис. 1.5).

,

.

Выберем , тогда механическая характеристика двигателя примет вид:

,

,

.

Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.

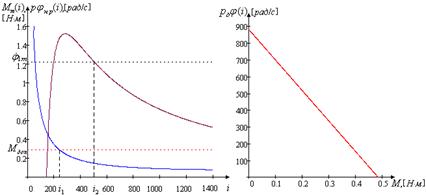
Рис. 1.4. Зависимость максимального момента Рис. 1.5. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора

Найдем граничные значения и , используя пакет MathCAD 2001:

.

При выборе конкретного значения передаточного числа i редуктора необходимо остановиться на минимально возможном значении из диапазона.

Для первого двигателя первой траектории выбираем .

  1.4.2 Второй двигатель для первой траектории

Подставим данные двигателя серия СД (таблица 1.5) в уравнение момента (1.27), получим зависимость максимального значения момента  от передаточного числа редуктора i:

,

.

Найдем значение номинального момента  по формуле 1.28:

.

Используя (1.24) найдем :

.

При помощи программного пакета MathCad построим графики зависимости максимального момента (рис. 1.6), а также по формуле 1.26 механическую характеристику (рис. 1.7).

,

.

Выберем , тогда механическая характеристика двигателя примет вид:

,

.

Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.

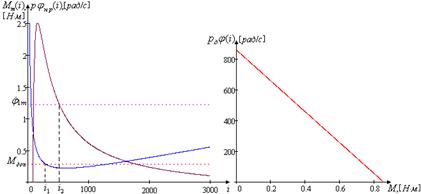
Рис. 1.6. Зависимость максимального момента Рис. 1.7. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора

Найдем граничные значения и , используя пакет MathCAD 2001:

.

Для второго двигателя первой траектории выбираем .

Проведя проверку на нагрев двигателей первой траектории, мы получили очень высокие значения передаточных чисел (, ). Выбор редуктора с таким передаточным отношением и при допустимой массе редуктора, не превышающей массу двигателя больше, чем в 2 раза, невозможен.