Первый двигатель второй траектории

1.4.3 Первый двигатель второй траектории

По формуле 1.23 найдем зависимость :

,

Подставим данные двигателя серии 2П (таблица 1.6) в уравнение момента (1.27), получим зависимость максимального значения момента  от передаточного числа редуктора i:

,

.

.

Используя (1.24) найдем :

.

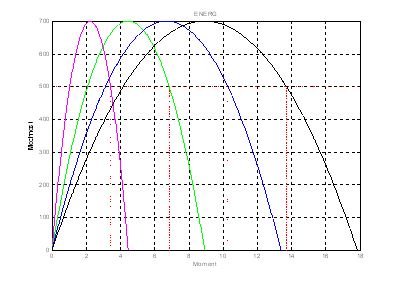
При помощи программного пакета MathCad построим графики зависимости максимального момента (рис. 1.8), а также по формуле 1.26 механическую характеристику (рис. 1.9).

,

.

Выберем , тогда механическая характеристика двигателя примет вид:

,

.

Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.

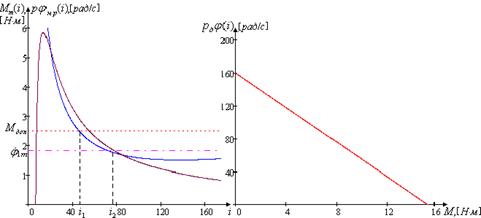
Рис. 1.8. Зависимость максимального момента Рис. 1.9. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора

Найдем граничные значения и , используя пакет MathCAD 2001:

.

Для первого двигателя второй траектории выбираем .

Наиболее подходящим по своим параметрам из найденных в справочных источниках информации редукторов является червячный одноступенчатый редуктор 5Ч 80 [2].

Основные характеристики выбранного редуктора:

– максимальный передаваемый крутящий момент ;

– коэффициент полезного действия ;

– подводимая расчетная мощность ;

– масса ;

– передаточное отношение ;

– габариты .

Максимальный передаваемый крутящий момент на тихоходном (выходном) валу редуктора к валу двигателя

 

.  (1.29)

Так, как значение момента  больше, чем величина допустимого момента на валу двигателя , следовательно, редуктор подобран верно.

  1.4.4 Второй двигатель второй траектории

Подставим данные двигателя серии ДВИ (таблица 1.6) в уравнение момента (1.27), получим зависимость максимального значения момента  от передаточного числа редуктора i:

.

Найдем значение номинального момента  по формуле 1.28:

.

Используя (1.24) найдем :

.

При помощи программного пакета MathCad построим графики зависимости максимального момента (рис. 1.10), а также по формуле 1.26 механическую характеристику (рис. 1.11).

,

.

Выберем , тогда механическая характеристика двигателя примет вид:

,

.

Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.

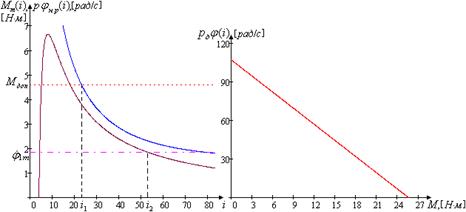
Рис. 1.10. Зависимость максимального момента Рис. 1.11. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора

Найдем граничные значения и , используя пакет Mathcad 2001:

.

Для второго двигателя второй траектории выбираем .

Наиболее подходящим по своим параметрам из найденных редукторов является цилиндрический двухступенчатый редуктор 1Ц2У 100 [4].

Характеристики выбранного редуктора:

– максимальный передаваемый крутящий момент ;

– коэффициент полезного действия ;

– масса ;

– передаточное отношение ;

– габариты .

Максимальный передаваемый крутящий момент на тихоходном (выходном) валу редуктора к валу двигателя определим по формуле 1.29:

Поскольку значение момента  больше, чем допустимый момент на валу двигателя , следовательно, редуктор подобран верно.

  1.5 Проверка двигателя привода на нагрев

Двигатель будет работать не перегреваясь, если среднее значение потерь его мощности в якорной цепи  за время рабочего цикла  не превышает потерь мощности в номинальном режиме :

. (1.30)

Среднее значение потерь мощности за время рабочего цикла  пропорционально квадрату среднего значения момента за названное время:

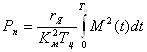. (1.31)

Из неравенства (1.30) и уравнения (1.31) следует, что условием нормального теплового режима двигателя является требование:

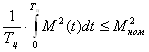, (1.32)

,

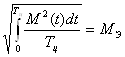где  – эквивалентный момент двигателя за время рабочего цикла, поэтому условие нормального теплового режима принимает вид

. (1.33)

Таким образом, при проверке двигателя на нагрев необходимо знать закон изменения момента двигателя,  в течение всего рабочего цикла. Разобьём рабочий цикл привода на характерные участки  и для каждого из них найдём описание . Эквивалентный момент двигателя находим в удобном для практического использования виде:

, (1.34)

. (1.35)

где  – эквивалентные моменты двигателя на соответствующих  участках цикла.

Режим разгон двигателя.

При проверке двигателя на нагрев необходимо учесть, что скорость двигателя не может изменяться мгновенно, поэтому траекторию необходимо сгладить в участках разгона и торможения. Максимально возможный момент двигателя определяется допустимой величиной тока в якорной цепи. Обычно

_, (1.36)

тогда и момент

.(1.37)

Моменту, развиваемому при разгоне, препятствует сила трения, поэтому ускорение в механизме:

. (1.38)

Время, необходимое для разгона:

. (1.39)

 

Режим торможение двигателя

Режиму торможения способствуют силы трения в механизмах поворота и силы тяжести нагрузки в механизмах подъема при подъеме груза. Двигатель должен развивать тот же максимально возможный момент . Ускорение, развиваемое двигателем при торможении в механизмах поворота и подъема груза в механизмах подъема:

. (1.40)

Время, необходимое для торможения

. (1.41)

  1.5.1 Проверка на нагрев первого двигателя первой траектории

Из рисунка 1.1 видно, что скорость в моменты времени t=2t₁ и t=13t₁ изменяется скачком. Двигатель не сможет обеспечить такой режим работы, поэтому необходимо предусмотреть участок разгона и участок торможения.

Разобьём время рабочего цикла на 7 интервалов времени:

1.  [0; t₁],

2.  [t₁; 2t₁-t_торм],

3.  [2t₁-t_торм; 2t₁],

4.  [2t₁; 13t₁],

5.  [13t₁; 13t₁+t_разг],

6.  [13t₁+t_разг; 14t₁],

7.  [14t₁; T_ц].

Режим разгона

Момент, развиваемый двигателем на участке разгона:

.

Для первого двигателя первой траектории .

По формуле 1.38 определим ускорение при разгоне:

.

Время, необходимое для разгона:

.

Режим торможения

На участке торможения двигатель должен развивать тот же максимально возможный момент .

По формуле 1.40 рассчитаем ускорение при торможении:

.

Время, необходимое для торможения:

.

Графики траектории, скорости и ускорения нагрузки, с учётом введённых участков разгона и торможения, показаны на рис. 1.12.

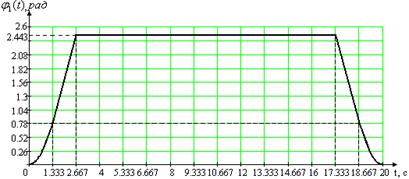
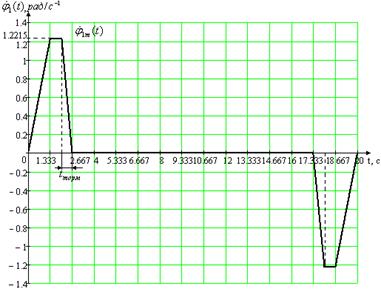
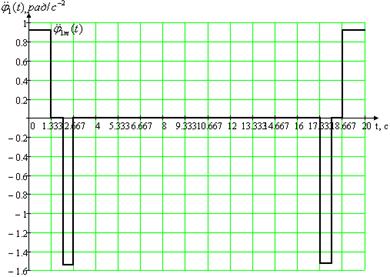
Рис. 1.12. Первая измененная траектория рабочего цикла

 

Состояние покоя

Момент, требуемый от двигателя на любом из участков траектории, определяется в соответствие с (1.14) и (1.23):

 (1.42)

Рассчитывая моменты для любого из участков траектории, рассуждаем следующим образом: составляющие уравнения 1.42, в которые входит ускорение, берем с теми знаками, как показывает диаграмма. Знак статического момента, приведенного к валу двигателя, выбираем так: если сопротивление нагрузки помогает режиму на данном участке (например, режим торможения), тогда знак статического момента берется противоположным знакам слагаемых, в которые входит . Если сопротивление нагрузки мешает (например, режим разгона), от двигателя требуется момент больший, значит, знак статического момента выбирается такой же, как у слагаемых, в которые входит .

Таблица 1.7

	Интервал времени	Формула для расчета	Значение
1			0.28687
2			0.00063
3			0.47771
4			0.00032
5			0.47771
6			0.00063
7			0.28561

При расчете момента  необходимо учесть то, что на участке  угловая скорость нагрузки p_1m(t) = 0, значит момент вязкого трения . Следовательно, статический момент на данном участке будет равен моменту сухого трения.

Из таблицы видно, что , а .

Находим эквивалентный момент двигателя по формуле (1.33):

.

Проверяем условие нормального теплового режима:

.

Поскольку условие выполняется, значит, двигатель типа ДВИ-211–02 с передаточным числом  подходит для данной траектории.

Определим энергетический запас двигателя, используемого при отработке первой траектории:

. (1.43)

.

  1.5.2 Проверка на нагрев второго двигателя первой траектории

Из пункта 1.4.2 возьмем значение номинального момента:

Режим разгона

Момент, развиваемый двигателем на участке разгона:

.

Для второго двигателя первой траектории .

По формуле 1.38 определим ускорение при разгоне:

.

Время, необходимое для разгона:

.

Режим торможения

На участке торможения двигатель должен развивать тот же максимально возможный момент .

По формуле 1.40 рассчитаем ускорение при торможении:

.

Время, необходимое для торможения:

.

Момент, требуемый от двигателя на любом из участков траектории, определяется по формуле 1.42.

Таблица 1.8

	Интервал времени	Формула для расчета	Значение
1			0.28547
2			0.00052
3			0.4771
4			0.00026
5			0.4771
6			0.00052
7			0.28443

Из таблицы видно, что , а .

Находим эквивалентный момент двигателя по формуле (1.33):

.

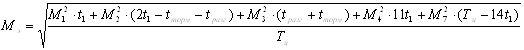
Проверяем условие нормального теплового режима:

.

Поскольку условие выполняется, значит, двигатель типа СД-150 с передаточным числом  подходит для данной траектории.

Определим энергетический запас двигателя: .

  1.5.3 Проверка на нагрев первого двигателя второй траектории

Из пункта 1.4.3 возьмем значение номинального момента:

Для второго двигателя первой траектории выбираем .

Момент, требуемый от двигателя на любом из участков траектории, определяется по формуле 1.42.

Таблица 1.8

	Интервал времени	Формула для расчета	Значение
1			2.485
2			-2.476
3			0.0017
4			-2.485
5			2.476

Находим эквивалентный момент двигателя по формуле (1.33):

.

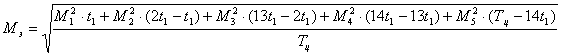
Проверяем условие нормального теплового режима:

.

Поскольку условие выполняется, значит, двигатель типа 2ПБ90МУХЛ4 с передаточным числом  подходит для второй траектории.

Определим энергетический запас двигателя:

.

1.5.4 Проверка на нагрев второго двигателя второй траектории

Из пункта 1.4.4 возьмем значение номинального момента:

Для второго двигателя первой траектории выбираем .

Момент, требуемый от двигателя на любом из участков траектории, определяется по формуле 1.42.

Таблица 1.9

	Интервал времени	Формула для расчета	Значение
1			4.442
2			-4.427
3			0.0032
4			-4.442
5			4.427

Находим эквивалентный момент двигателя по формуле (1.33):

,

.

Проверяем условие нормального теплового режима:

.

Поскольку условие выполняется, значит, двигатель типа ДВИ-321–02 с передаточным числом  подходит для второй траектории, т.е. с двигателем при отработке траектории не произойдет перегрева.

Определим энергетический запас двигателя:

.

  1.6 Выбор рабочей траектории

Для выбора программной траектории движения нагрузки необходимо проанализировать достоинства и недостатки каждой из двух возможных траекторий, а также пар двигателей, чтобы в итоге остановиться на одной траектории и выбрать один из четырех двигателей.

Сравним двигатели, выбранные для данных траекторий. Скорости вращения двигателей типа ДВИ-211–02 и СД-150 для первой траектории очень большие ( и  соответственно), нежели для второй траектории ( и ). Чем ниже скорость вращения двигателя, тем меньшее передаточное число требуется обеспечить, а, следовательно, выбрать более простой редуктор, подходящий по массогабаритным характеристикам и его КПД.

Как для первой, так и для второй траектории, все двигатели обеспечивают достаточный энергетический запас, но двигатели для второй траектории типа 2ПБ90МУХЛ4 и ДВИ-321–02 обеспечивают больший запас энергии.

Необходимо отметить, что изменения, которым подвергается первая программная траектория, снижают качество управляемого привода.

Остановим свой выбор на второй из двух возможной траекторий.

Для второй траектории движения необходимо выбрать двигатель из двух возможных 2ПБ90МУХЛ4 и ДВИ-321–02. Сравнивая технические характеристики двигателей (таблица 1.6), можем отметить, что двигатель 2ПБ90МУХЛ4 обладает меньшей массой по сравнению с двигателем ДВИ-321–02, и меньшим сопротивлением в якорной цепи, что уменьшает тепловые потери, и меньшим энергетическим запасом.

Таким образом, выбираем двигатель типа 2ПБ90МУХЛ4 и соответственно подобранный для него редуктор 5Ч 80 типа червячный одноступенчатый с передаточным отношением .

 
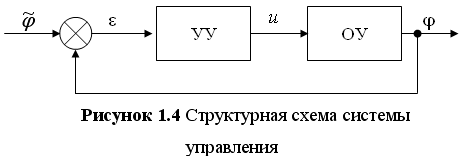
2. Синтез системы управления электроприводом   2.1 Выбор информационных элементов привода

Информационными элементами привода являются элементы измерителя рассогласований: задающее устройство, датчик обратной связи, сумматор.

Вид управляемого привода обуславливает выбор типа информационных элементов: датчиков линейных или угловых перемещений.

Приведем статическую ошибку системы, заданную в ТЗ в относительных единицах, к абсолютным единицам.

. (2.1)

Допустимая погрешность измерителя рассогласования  находится по заданной в ТЗ статической погрешности привода , которая складывается из статических погрешностей привода по задающему и возмущающему воздействиям, статической погрешности измерителя рассогласований и погрешностей элементов прямого канала привода: усилителя мощности, преобразователя, двигателя, редуктора. Точность измерителя рассогласования удовлетворительна, если составляет не более трети допустимой статической погрешности, оговариваемой ТЗ на проектируемый привод.

. (2.2)

Ошибка измерителя рассогласования  определяется способом среднеквадратического суммирования ошибок задающего устройства (ЗУ) и датчика обратной связи (ДОС).

 (2.3)

Будем считать, что датчики ДОС и ЗУ абсолютно идентичны, поэтому они вносят одинаковый вклад в статическую ошибку измерителя рассогласования.

 (2.4)

Тогда из выражения 2.4 статические ошибки ДОС и ЗУ:

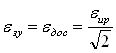. (2.5)

При выборе информационных элементов необходимо исходить из требований технического задания на разработку привода:

·  вида управляемого привода и статической погрешности датчика ,

·  максимальных перемещений ,

·  скорости .

Исходя из выше изложенных требований к информационным элементам, выберем потенциометр проволочный, характеристики которого представлены в таблице 2.1.

Таблица 2.1. Параметры выбранного датчика

Серия	ПЛП-8
Тип	Круговой
Максим. допустимая скорость движения	18 об/мин
Максимальная накопленная погрешность
Диапазон измеряемых перемещений
Масса, кг	2.0

  2.2 Синтез структурной схемы управляемого привода

Синтез структурной схемы привода начинают с разработки его функциональной схемы.

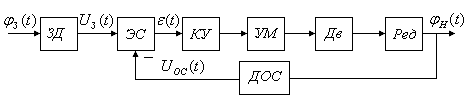
Рис. 2.1. Функциональная схема управляемого привода

На рис. 2.1 обозначено:

ЗД − задающий датчик (преобразовывает механический сигнал в электрический);

ЭС − элемент сравнения (в данном случае сумматор);

КУ − корректирующее устройство;

УМ − усилитель мощности (формирует напряжение в якорную цепь двигателя);

Дв – двигатель, преобразующий напряжение на его входе в угловое перемещение на его выходном валу;

Ред – редуктор, понижающий значение углового перемещения на выходном валу двигателя до величины перемещения, необходимого для управления положением рабочей нагрузки;

ДОС – датчик обратной связи, обеспечивающий преобразование физического сигнала в форму, удобную для сравнения.

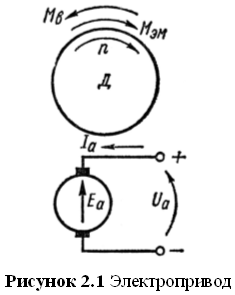
Линеаризованная структурная схема двигателя постоянного тока (ДПТ) с независимым возбуждением при управлении по цепи якоря, составленная для приращений переменных двигателя в относительных единицах (о.е.), представлена на рис. 2.2.

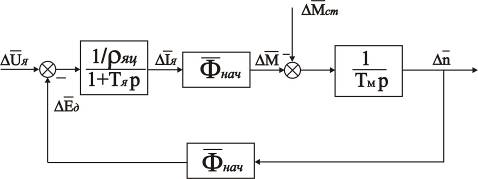
Рис. 2.2. Линеаризованная структурная схема ДПТ в о.е.

На схеме (рис. 2.2) обозначено:

 – приращение напряжения управления, .

 – приращение ЭДС, .

 – приращение тока в цепи якоря, .

 – значение магнитного потока двигателя в рабочей точке.

. (2.6)

 

 – относительное сопротивление якорной цепи.

. (2.7)

 – приращение приведенного к валу двигателя статического момента нагрузки, .

 – приращение момента, развиваемого двигателем, .

 – постоянная якорной цепи, определяемая отношением реактивного  и активного  сопротивлений цепи.

 – приращение угловой скорости вала двигателя, .

 – механическая постоянная двигателя.

, (2.8)

где  – динамический момент инерции на валу двигателя,

. (2.9)

За базовые значения угловой скорости вала двигателя , момента двигателя , напряжения  и тока в цепи якоря  принимают их номинальные значения.

Двигатель имеет переменный параметр – , меняющийся от некоторого минимального  до максимального значения  вслед за изменением моментов нагрузки. При синтезе управляющего устройства выбирают регулятор, способный обеспечить требуемое качество управления приводом при любом значении  из известного диапазона. Величину статического момента нагрузки , являющегося возмущающим воздействием для двигателя, при синтезе привода принимают максимальной.

Для использования структурной схемы двигателя в общей структуре привода необходимо осуществить в схеме переход от относительных единиц измерения (о.е.) к абсолютным единицам (а.е.).

Передаточные функции двигателя по управляющему и возмущающему воздействиям в а.е. могут быть получены из соответствующих им выражений в о.е. при использовании базовых значений параметров, выбранных для совершения прямого перехода в схеме.

За базовое значение магнитного потока двигателя  примем его номинальное значение . Рабочее значение магнитного потока  выбираем в рабочем интервале . Пусть .

Используя структурную схему двигателя в относительных единицах (рис. 2.2) и приведенные выше базовые значения переменных, преобразуем схему, введя масштабирующие коэффициенты, обеспечивающие измерение в абсолютных единицах передаточных функций двигателя по управляющему  и возмущающему  воздействиям (рис. 2.3).

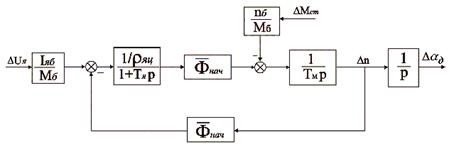
Рис. 2.3. Линеаризованная структурная схема ДПТ с передаточными функциями в абсолютных единицах (а.е.)

Приведем все необходимые параметры для дальнейших расчетов схемы.

Двигатель 2ПБ90МУХЛ4

;

;

;

;

;

;

;

;

.

Редуктор червячный одноступенчатый 5Ч 80

;

.

Траектория рабочего цикла

;

;

;

;

.

Магнитный поток двигателя в рабочей точке (формула 2.6):

.

.

 

Относительное сопротивление якорной цепи (формула 2.7):

Возмущающее воздействие

;

.

Для нахождения механической постоянной двигателя  определим суммарные минимальное и максимальное значения момента инерции на валу двигателя согласно формуле 2.9:

,

.

 

Минимальное и максимальное значение механической постоянной двигателя

,

.

Передаточная функция двигателя по управляющему воздействию

,

,

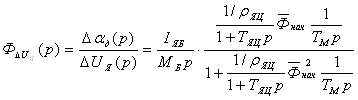Разделим числитель и знаменатель передаточной функции на :

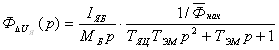, где .

Найдем минимальное и максимальное значение электромеханической постоянной времени двигателя :

,

.

Заметим, что если представить, что , тогда полученная передаточная функция эквивалентна передаточной функции колебательного звена:

. (2.10)

Если  < 1, то выражение (2.10) – произведение передаточных функций интегратора и колебательного звена.

Если   1, то выражение (2.10) – произведение передаточных функций интегратора и двух последовательно соединенных апериодических звеньев.

Определим параметры данной передаточной функции из следующей пары уравнений:

, (2.11)

. (2.12)

Из уравнения 2.12 выразим параметр :

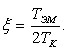 (2.13)

Из уравнения (2.11) определим минимальное и максимальное значения постоянной времени :

 

,

.

Определим значения параметра  при максимальном и минимальном значениях механической постоянной времени:

 

,

.

Найденные значения , поэтому представим передаточную функцию двигателя как передаточную функцию двух последовательно соединенных апериодических звеньев. Для этого решим уравнения:

, (2.14)

 (2.15)

Решим уравнение (2.14):

.

Корни уравнения:

,

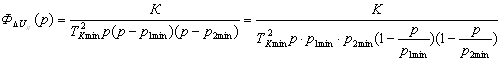где .

.

. (2.16)

Аналогично решим уравнение 2.15:

Корнями данного уравнения являются:

Таким образом, получим:

.

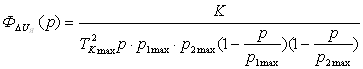Определим коэффициент передачи двигателя:

 

.

. (2.17)

 

Передаточная функция двигателя по возмущающему воздействию

 

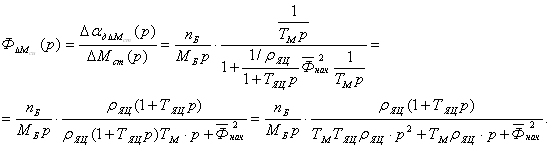
Разделим числитель и знаменатель передаточной функции на :

.

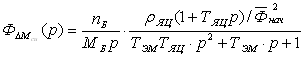. (2.18)

Заметим, что знаменатель передаточной функции двигателя по возмущающему воздействию совпадает со знаменателем передаточной функции по управляющему воздействию. Поэтому представим знаменатель функции (2.18) в следующем виде:

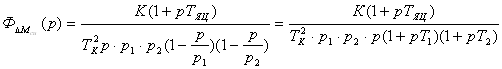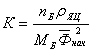, где .

, где .

Коэффициенты передачи двигателя:

,

,

.

Для дальнейшего использования составим таблицу со всеми найденными параметрами передаточных функций двигателя (таблицу 2.2).

Таблица 2.2. Значения параметров ПФ двигателя

Параметр	Значения
ТМ, c	3.196	3.936
ТЭМ, c	0.686	0.845
ТК, c	0.1257	0.1395
	2.727	3.027
Т1, c	0.024	0.821
Т2, c	0.662	0.024
КДВ Вб-1 (ПФ по управляющему воздействию)	3.501
КДВ, Вб-1 (ПФ по возмущению)	21.5232

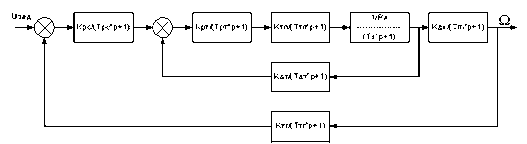
Изобразим структурную схему управляемого привода (рис. 2.4).

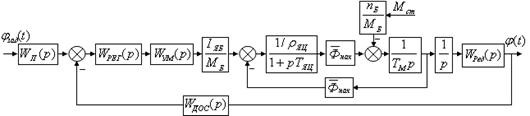
Рис. 2.4. Структурная схема управляемого привода

Передаточные функции отдельных звеньев привода:

–  – передаточная функция задающего устройства;

–  – передаточная функция корректирующего устройства;

–  – передаточная функция усилителя мощности;

– – передаточная функция двигателя по управляющему воздействию;

–– передаточная функция двигателя по возмущающему воздействию;

–  – передаточная функция редуктора;

– – передаточная функция датчика обратной связи.

  2.3 Синтез структуры регулятора

В структуре управляемого привода два модуля: силовой и управляющий. Управляющий модуль состоит из измерителя рассогласований и регулятора. Для того чтобы система удовлетворяла требованиям технического задания, необходимо провести синтез регулятора.

При помощи правил преобразования структурной схемы, перенесем звено  через первый сумматор, при этом необходимо включить звено  в обратную связь. Поскольку , преобразовав, таким образом, схему, мы получим единичную отрицательную обратную связь. Аналогично перенесем второй сумматор через два звена:  и , добавив эти звенья в локальную обратную связь.

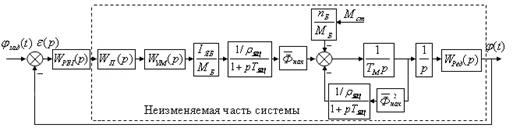
Рис. 2.5. Преобразованная структурная схема привода

Запишем передаточную функцию неизменяемой части системы:

, (2.19)

где  – коэффициент исходной системы без учета регулятора.

Выражение 2.19 при минимальной и максимальной нагрузках примет следующий вид:

, (2.20)

. (2.21)

Проанализируем устойчивость исходной системы и соответствие системы требованиям по качеству. Об устойчивости системы можно судить по ее реакции на единично ступенчатую функцию, т.е. по ее переходной характеристике. Построим соответствующие графики в программном пакете MATLAB. Графики переходной характеристики представлены на рис. 2.6 – 2.7.

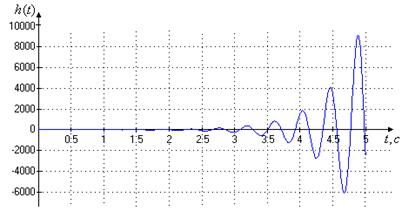
Рис. 2.6. Переходная характеристика исходной системы при минимальной нагрузке на управляемый привод

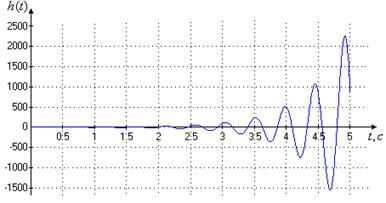
Рис. 2.7. Переходная характеристика исходной системы при максимальной нагрузке на управляемый привод

Таким образом, мы получили, что исходная система не устойчива. Необходимо введение в исходную систему корректирующего устройства (КУ) для обеспечения требуемого качества как в установившемся (задано в виде динамической ошибки), так и в переходном (ограничения на прямые показатели качества) режимах.

Проведем синтез при помощи метода логарифмических амплитудно-частотных характеристик (ЛАЧХ). Разобьем синтез на условные стадии:

1)  Построение ЛАЧХ исходной системы.

2)  Построение желаемой ЛАЧХ в соответствие с требованиями ТЗ.

3)  Определение передаточной функции КУ.

1) Для построения логарифмических амплитудно-частотных характеристик (ЛАЧХ) неизменяемой части системы проведем расчеты.

.

Осуществим переход: . Тогда выражение для построения ЛАЧХ примет вид:

.

.

.

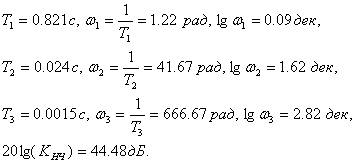
2)  В ТЗ заданы относительная динамическая ошибка, максимальные скорость и ускорение траектории движения. В соответствие с этим для построения границы запретной области необходимо найти координаты контрольной точки .

. (2.22)

. (2.23)

В соответствие с (2.22–2.23) найдем .

, , .

Таким образом, .

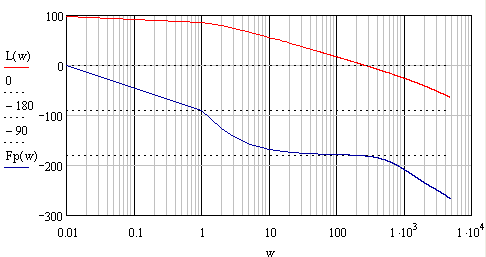
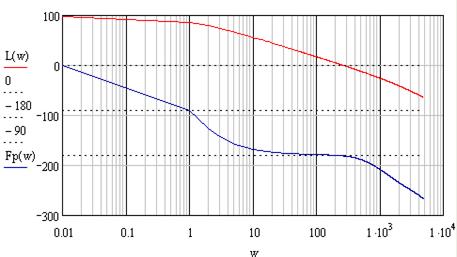
Для того чтобы входное воздействие воспроизводилось с ошибкой, не превосходящей динамическую ошибку, ЛАЧХ системы не должна попадать в запретную область. По рис. 2.8 можно сделать вывод о выполнении требования ТЗ по качеству системы в установившемся режиме, т.к. при минимальном и максимальном значениях электромеханической постоянной двигателя  ЛАЧХ располагаемой разомкнутой системы не заходит в запретную область. Однако система не удовлетворяет требуемому качеству в переходном режиме .

Среднечастотный участок определяет устойчивость и запасы устойчивости системы, а, следовательно, и качество системы в переходном режиме. Для построения среднечастотного участка будем использовать методику Бесекерского [3, с. 369].

Для определения левой и правой границ среднечастотного участка используются неравенства:

, (2.24)

где 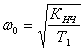 – базовая частота,

– показатель колебательности.

Значение  определим по номограмме [3, c.378]: .

Подставим значения в формулу 2.24:

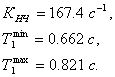
В формулу подставляем значение показателя колебательности: .

Таким образом, ,

.

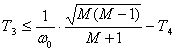, (2.25)

где .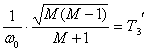

Сначала рассчитаем значение  и сравним его с постоянными времени исходной системы.

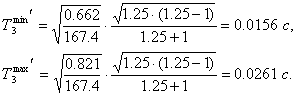
Для вычисления  необходимо вычесть из  постоянные времени исходной системы, меньшие чем .

Исходные данные:

По правилу сначала нужно вычесть наименьшие постоянные времени, поэтому отнимем от  только  исходной системы:

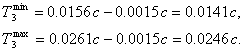
Найдем значение  из формулы 2.25:

Таким образом, мы рассчитали значения границ среднечастотного участка:

,

 

Расширяя среднечастотный участок, мы добьемся требуемого качества в переходном режиме. Левую границу будем смещать до тех пор, пока не будет выполняться требуемое значение запаса по модулю , которое необходимо выбрать по заданному значению перерегулирования по номограмме [3, с. 358]: . Правая граница должна обеспечить запас как минимум .

Высокочастотный участок определяет помехозащищенность системы, поэтому наклон высокочастотных асимптот должен быть большим. В то же время с целью упрощения модели корректирующего устройства высокочастотные асимптоты  выполняют параллельными высокочастотным асимптотам исходной характеристики, то есть на частоте  наклон становится 80 – дБ/дек.

3) Определим передаточную функцию регулятора. Построение  представлено на рис. 2.8.

Определим передаточную функцию последовательного КУ:

. (2.26)

Составим передаточную функцию  по виду:

,

.

По формуле 2.26 найдем :

.

 
2.4 Обеспечение требуемой точности проектируемого привода

В ТЗ на проектирование указаны допустимые статическая  и динамическая  ошибки привода.

Статическая ошибка системы оценивается в типовом режиме: при постоянных значениях задающего и возмущающего воздействий. В п. 2.1 уже использовалась допустимая  при выборе элементов измерителя рассогласований. На измеритель рассогласования была выделена третья часть . Оставшиеся две трети  составляют: статическая ошибка элементов прямого канала системы (усилителя, двигателя, редуктора), ошибки системы по задающему и возмущающему воздействиям. В соответствии с вышесказанным, уравнение статической ошибки системы:

, (2.27)

где  – ошибка элементов прямого канала,

 – ошибка по задающему воздействию,

 – ошибка по возмущению.

Таким образом, статическая погрешность элементов прямого канала .

Статическая погрешность по задающему значению , так как система является астатической по задающему воздействию.

Статическая погрешность привода по возмущающему воздействию  – .

Определим допустимую статическую погрешность привода по возмущающему воздействию:

.

Для определения ошибки скорректированной системы по возмущающему воздействию воспользуемся методом коэффициентов ошибок, описываемым формулой [3, с. 198]:

, (2.28)

где  – передаточная функция замкнутой системы по ошибке относительно возмущения ,

 – статический момент нагрузки приведенного к валу двигателя, являющийся возмущающим воздействием ().

Найдем передаточную функцию  по структурной схеме (рис. 2.5) скорректированной системы управляемого привода.

.

.

.

.

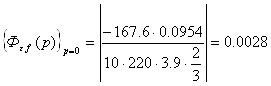Таким образом, получили, что , значит, рассчитанный коэффициент передачи корректирующего устройства удовлетворяет требованиям к статической точности системы.

Далее проведем оценку динамической точности системы. Допустимая динамическая ошибка системы  указывает заданную точность воспроизведения программного входного сигнала.

Амплитуда ошибки определяется по формуле:

, (2.29)

где  – ордината контрольной точки запретной области, найденная в пункте 2.3.

Найдем значение динамической ошибки при минимальной и максимальной нагрузках на управляемый привод:

,

.

Таким образом, рассчитанная динамическая ошибка системы  меньше, чем динамическая ошибка системы, заданная в ТЗ . Значит, скорректированная система удовлетворяет требованиям ТЗ по динамической точности при максимальной массе нагрузки.

 
3. Моделирование спроектированного управляемого привода   3.1 Модель скорректированной системы при отработке ступенчатого сигнала   3.1.1 Цифровая модель скорректированной системы при отработке ступенчатого сигнала при минимальной нагрузке на управляемый привод

На рис. 3.1 приведена цифровая модель скорректированной системы при отработке ступенчатого сигнала при минимальной нагрузке на управляемый привод, разработанная в программном пакете MATLAB версии 7.3.

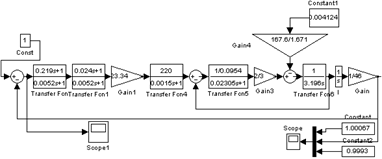
Рис. 3.1. Цифровая модель скорректированной системы при отработке ступенчатого сигнала при минимальной нагрузке на управляемый привод

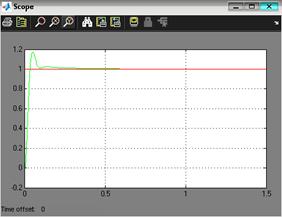
Рис. 3.2. Реакция выхода системы на единичный ступенчатый сигнал при минимальной нагрузке

По графику (рис. 3.2) найдем установившееся и максимальное значения :

Расчетное выражение для перерегулирования:

. (3.1)

Для определения время регулирования  построим «коридор»:

. (3.2)

Определим прямые показатели качества желаемой системы при минимальной массе нагрузки на проектируемый привод и сравним с соответствующими значениями, заданными в ТЗ:

Требования ТЗ:

,

.

Реальные значения показателей определим по формулам 3.1 – 3.2:

,

.

Границы коридора: ,

Статическую ошибку системы можно определить по графику ошибки, представленном на рис. 3.3.

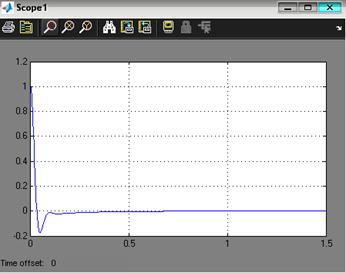
Рис. 3.3. Ошибка системы при отработке ступенчатого сигнала при минимальной массе нагрузки на управляемый привод

В ТЗ определена статическая допустимая погрешность: .

. (3.3)

 

Реальное значение ошибки: .

3.1.2 Цифровая модель скорректированной системы при отработке ступенчатого сигнала при максимальной нагрузке на управляемый привод

Цифровая модель скорректированной системы при отработке ступенчатого сигнала при максимальной массе нагрузки на управляемый привод представлена на рис. 3.4.

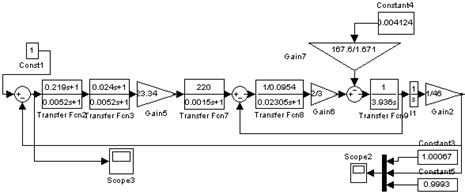
Рис. 3.4. Цифровая модель скорректированной системы при отработке ступенчатого сигнала при максимальной нагрузке на управляемый привод

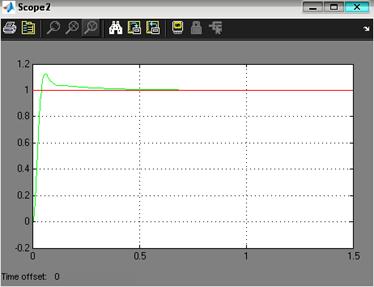
Рис. 3.5. Реакция выхода системы на единичный ступенчатый сигнал при максимальной нагрузке

По графику (рис. 3.5) найдем установившееся и максимальное значения :

Реальные значения показателей:

,

.

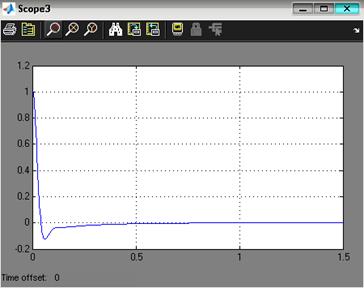
Рис. 3.6. Ошибка системы при отработке ступенчатого сигнала при максимальной массе нагрузки на управляемый привод

Результаты моделирования приведены в приложении 5.

Реальное значение ошибки: .

Требование ТЗ к статической точности: .

Проанализировав найденные показатели качества скорректированной системы, можно сделать, что полученная скорректированная система удовлетворяет заданным требованиям к качеству переходного процесса и статической точности, как при минимальной, так и при максимальной массе нагрузки на управляемый привод.

 
3.2 Модель желаемой системы при отработке выбранной траектории   3.2.1 Цифровая модель скорректированной системы при отработке выбранной траектории движения при минимальной нагрузке на управляемый привод

На рис. 3.7 представлена цифровая модель скорректированной системы при отработке выбранной траектории движения при минимальной массе нагрузки, построенная в программной среде MATLAB.

Рис. 3.7. Цифровая модель скорректированной системы при отработке программной траектории при минимальной нагрузке на управляемый привод

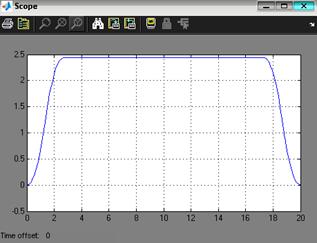
Рис. 3.8. Реакция выхода системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод

Динамическую ошибку системы определим по графику ошибки, представленном на рисунке 3.9.

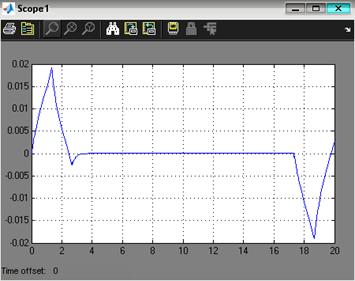
Рис. 3.9. Ошибка системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод

 

Реальное значение ошибки:

Требование ТЗ к динамической точности: .

3.2.2 Цифровая модель скорректированной системы при отработке программной траектории движения при максимальной массе нагрузки на управляемый привод

На рис. 3.10 представлена цифровая модель скорректированной системы при отработке выбранной траектории движения при максимальной массе нагрузки, построенная в программном пакете MATLAB.

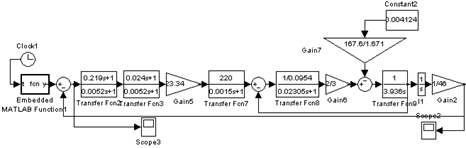
Рис. 3.10. Цифровая модель скорректированной системы при отработке программной траектории при максимальной нагрузке на управляемый привод

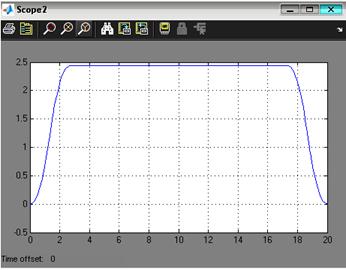
Рис. 3.11. Реакция выхода системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод

Динамическую ошибку системы определим по графику ошибки, представленном на рисунке 3.12.

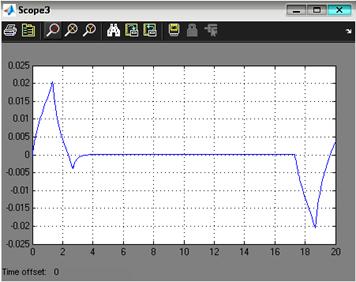
Рис. 3.12. Ошибка системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод

 

Реальное значение ошибки:

Требование ТЗ к динамической точности: .

Цифровая модель спроектированного электропривода для максимальной и минимальной массы нагрузки удовлетворяет ограничению на динамическую ошибку, представленному в ТЗ.

 
Заключение

В курсовом проекте был разработан электропривод, предназначенный для программного управления линейным перемещением механизма подъёма промышленного робота-манипулятора.

При выполнении первого этапа проекта рассматривались две программные траектории перемещения нагрузки, предложенные в техническом задании, для которых были рассчитаны параметры (скорость, ускорение). Для каждой из траекторий были определены нагрузки, действующие на привод, выбран двигатель и редуктор, проведена проверка двигателя и редуктора на нагрев. Далее ввиду функциональных особенностей привода была выбрана оптимальная траектория.

На втором этапе проектирования выбраны информационные элементы (потенциометры) по заданной статической точности, проведен синтез регулятора.

На следующем этапе был проведено моделирование цифровой модели спроектированного электропривода с помощью программного пакета MATLAB. Полученная цифровая модель отвечала всем требованиям технического задания по точности и качеству. Соответствие характеристик рассчитанной системы требованиям технического задания приведено в таблице 4.

Таблица 4. Сравнение результатов, полученных при выполнении проекта

Основные требования	По требованиям ТЗ	Скорректированная система
			14.81
			11.04
			0.87
			0.95
			0.001
			0.001
			0.78
			0.83

Спроектированный электропривод удовлетворяет всем требованиям ТЗ как при минимальной, так и при максимальной массах нагрузки.

Список литературы

1.  Подлинева Т.К., Устюгов М.Н. Проектирование управляемого привода в электромеханических системах: Учебное пособие по курсовому проектированию.

2.  http://www.izh-reduktor.ruproductionscherv_reductsreduktoryi _odnostupenchatyie _tipa_5ch.html.

3.  Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – СПб: Профессия, 2003 – 752с.

4.  http://www.1000a.ru/catalog-12.htm.