Навигация
Определим устойчивость при T1 = T2 = 1 c и kv = 1 c-1
5. Определим устойчивость при T1 = T2 = 1 c и kv = 1 c-1.
![]()
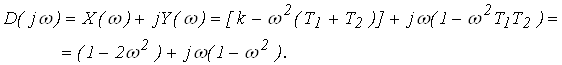
5. Строим характеристическую кривую![]() (рис. 5) по данным, приведенным в таблице 1.
(рис. 5) по данным, приведенным в таблице 1.
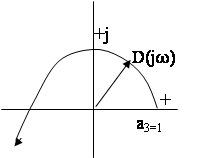
Таблица 1
| w | 0 |
| 1 | ¥ | ||
| X(w) | 1 | 0 | -1 | -¥ | ||
| 0 |
| 0 | -¥ |
В соответствии с критерием Михайлова, рассматриваемая система является устойчивой.
4. Частотный критерий устойчивости Найквиста
Частотный критерий устойчивости Найквиста позволяет по виду частотной характеристики разомкнутой системы судить об устойчивости замкнутой системы, т.е. он применим для замкнутых систем.
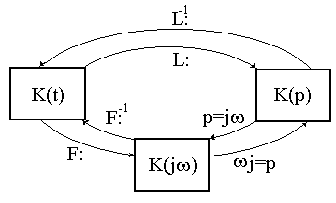
Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых систем
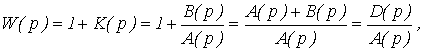 (6)
(6)
где D(p) – характеристический полином замкнутой системы;
A(p) – характеристический полином разомкнутой системы.
При этом степени полиномов A(p) и D(p) одинаковы исходя из условия физической реализуемости системы.
В соответствии со следствием из принципа аргумента
![]() (7)
(7)
Рассмотрим разные случаи.
Система, устойчивая в разомкнутом состоянии.
Так как разомкнутая система устойчива, то она не содержит корней в правой полуплоскости (т.е. m = 0), для того чтобы и замкнутая система была устойчива, должно выполняться условие:
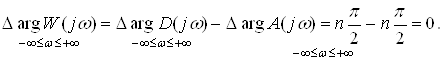 (8)
(8)
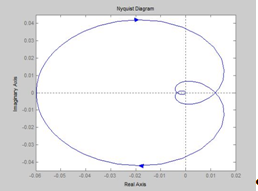
Графически это обозначает, что годограф вектора W (jw) не охватывает начала координат, а вектора K (jw) – точку с координатами (-1, j0), как показано на рис. 6. Точка с координатами (-1, j0) называется критической.

Рис. 6.
Система, неустойчивая в разомкнутом состоянии.
Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того, чтобы замкнутая система была устойчивой, должно выполняться условие
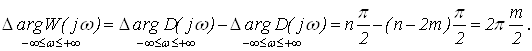 (9)
(9)
Графически это обозначает, что годограф вектора K (jw) охватывает точку с координатами (-1, j0) m/2 – раз.
Формулировка критерия Найквиста: Замкнутая система автоматического управления устойчива, если амплитудно-фазовая частотная характеристика разомкнутой, неустойчивой системы, имеющей m корней в правой полуплоскости, охватывает точку с координатами (–1, j0) m/2-раз.
Иногда по графику трудно определить охватывает ли АФХ критическую точку. В этом случае можно использовать правило переходов. Переходами называются точки пересечения АФХ отрезка оси (-¥.. – 1). Знак перехода определяется по следующему правилу: если фаза убывает – переход отрицательный.
Формулировка критерия Найквиста: Замкнутая система автома-тического управления устойчива, если разность положительных и отрицательных переходов равна m/2, где m – количество корней в правой полуплоскости разомкнутой неустойчивой системы, т.е.
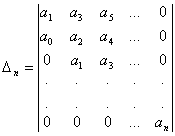
|
(10)
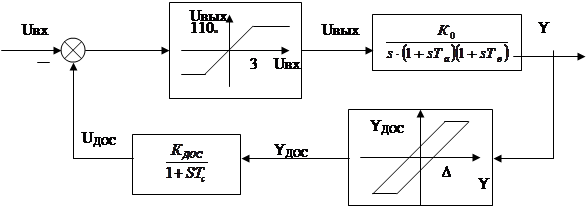
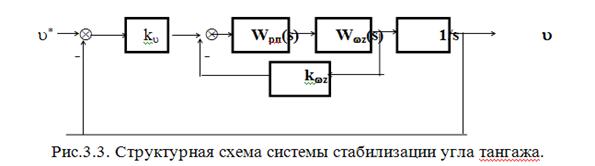
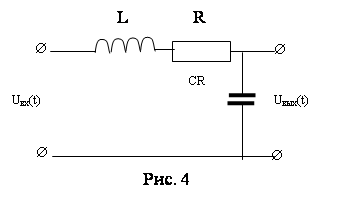
Пример 8. Для заданной системы (рис. 7) определить условие устойчивости и критический коэффициент усиления.
Определить устойчивость при T1 = T2 = 1 c и kv = 1 c-1.
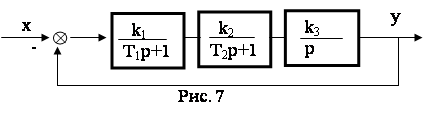
Решение:
Похожие работы
... записи в Zam_ck=inv(l+sysl)*sysl можно в диалоговом режиме произвести новую запись zpk(.) - сокращая одинаковые элементы числителя и знаменателя в Zam_ck. 2.Исследование линейной импульсной системы автоматического управления Задание: 1) Найти передаточные функции импульсной САУ: W*(z) разомкнутой системы, Ф*(z) – замкнутой системы, Фе*(z) – системы по ошибке. Параметры Т, Т1, τ1, К0, ...
... устройства, которое нужно добавить к некоторой неизменяемой части системы, чтобы обеспечит требуемое качество системы в установившемся и переходном режимах. Наиболее приемлемым для решения задачи динамического синтеза является метод логарифмических амплитудных характеристик (метод ЛАХ). [1, § 12.5] Стадии синтеза по методу ЛАХ включают: 1. построение располагаемой ЛАХ, т.е. ЛАХ исходной ...
... можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость. Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением. Построение области ...
... значениях функции. Начальное значение функции:. (2.10) Конечное значение функции: . (2.11) 7. Теорема запаздывания . (2.12) 4. Дифференциальные уравнения САУ При математическом описании систем автоматического управления составляют уравнения статики и динамики. Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими. Уравнения динамики ...

0 комментариев