Навигация
Расчёт закона управления продольным движением самолета
Кафедра: ТАУ
РАСЧЁТ ЗАКОНА УПРАВЛЕНИЯ ПРОДОЛЬНЫМ ДВИЖЕНИЕМ САМОЛЁТА
Оглавление
Введение
1. Математическое описание продольного движения самолета
1.1 Общие сведения
1.2 Уравнения продольного движения самолета
1.3 Силы и моменты при продольном движении
1.4 Линеаризованные уравнения движения
1.5 Математическая модель привода стабилизатора
1.6 Математические модели датчиков угловой скорости и перегрузки
1.7 Математическая модель датчика положения штурвала
2. Техническое задание на разработку алгоритма ручного управления продольным движением самолета
2.1 Общие положения
2.2 Требования к статическим характеристикам
2.3 Требования к динамическим характеристикам
2.4 Требования к разбросам параметров
2.5 Дополнительные требования
3. План выполнения курсовой работы
3.1 Этап анализа
3.2 Этап синтеза
4. Рекомендации к выбору желаемых собственных значений
Введение
Целью курсовой работы является закрепление материала первой части курса ТАУ [1] и освоение модальной методики расчета алгоритмов управления на примере синтеза закона управления продольным движением самолета. Методические указания содержат вывод математических моделей продольного движения самолета, электрогидравлического привода руля высоты, датчиков положения штурвала, угловой скорости тангажа, перегрузки, а также приводятся числовые данные для гипотетического самолета.
Одним из наиболее ответственных и трудных моментов при реализации методики модального синтеза является выбор желаемых собственных значений. Поэтому приведены рекомендации по их выбору.
1. Математическое описание продольного движения самолета
1.1 Общие сведения
Полет самолета осуществляется под влиянием сил и моментов, действующих на него. Отклоняя органы управления, летчик может регулировать величину и направление сил и моментов, тем самым, изменяя параметры движения самолета в желаемую сторону. Для прямолинейного и равномерного полета необходимо, чтобы все силы и моменты были уравновешены. Так, например, в прямолинейном горизонтальном полете с постоянной скоростью подъемная сила равна силе тяжести самолета, а тяга двигателя – силе лобового сопротивления. При этом обязательно должно соблюдаться и равновесие моментов. В противном случае самолет начинает вращаться.
Равновесие, созданное летчиком, может быть нарушено воздействием какого-либо возмущающего фактора, например, турбулентностью атмосферы или порывами ветра. Поэтому когда режим полета установлен, требуется обеспечить устойчивость движения.
Другой важнейшей характеристикой самолета является управляемость. Под управляемостью самолета понимают его способность реагировать на перемещение рычагов управления (органов управления). О хорошо управляемом самолете летчики говорят, что он хорошо «ходит за ручкой». Это означает, что для выполнения требуемых маневров летчику необходимо совершить простые по характеру отклонения рычагов и прилагать к ним небольшие по величине, но четко ощутимые усилия, на которые самолет отвечает соответствующими изменениями положения в пространстве без излишнего запаздывания. Управляемость – важнейшая характеристика самолета, определяющая возможность полета. На неуправляемом самолете летать невозможно.
Летчику одинаково трудно управлять самолетом, когда требуется прикладывать большие усилия к рычагам управления и выполнять большие перемещения штурвала, а также когда отклонения штурвала и усилия, потребные для их отклонения, слишком малы. В первом случае летчик быстро утомляется при совершении маневров. О таком самолете говорят, что он «тяжел в управлении». Во втором случае самолет реагирует на малое, иногда даже непроизвольное перемещение ручки, требуя от летчика большого внимания, точного и плавного управления. О таком самолете говорят что он «строг в управлении» [2].
На основе летной практики и теоретических исследований установлено, какими должны быть характеристики устойчивости и управляемости, чтобы удовлетворить требованиям удобного и безопасного пилотирования. Один из вариантов формулирования этих требований представлен в техническом задании на курсовую работу.
1.2 Уравнения продольного движения самолетаОбычно полёт самолёта рассматривают как движение в пространстве абсолютно жёсткого тела. При составлении уравнений движения используют законы механики, позволяющие в самом общем виде записать уравнения движения центра масс самолёта и его вращательного движения вокруг центра масс.
Исходные уравнения движения вначале записывают в векторной форме
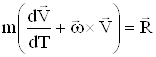 ,
,
![]() ,
,
где
m – масса самолета;
![]() – равнодействующая всех сил;
– равнодействующая всех сил;
![]() – главный момент внешних сил самолёта, вектор суммарного вращающего момента;
– главный момент внешних сил самолёта, вектор суммарного вращающего момента;
![]() – вектор угловой скорости системы координат;
– вектор угловой скорости системы координат;
![]() – момент количества движения самолёта;
– момент количества движения самолёта;
t – время.
Знак «![]() » обозначает векторное произведение. Далее переходят к обычной скалярной записи уравнений, проектируя векторные уравнения на некоторую систему координатных осей.
» обозначает векторное произведение. Далее переходят к обычной скалярной записи уравнений, проектируя векторные уравнения на некоторую систему координатных осей.
Получаемые общие уравнения оказываются настолько сложными, что, по существу, исключают возможность проведения наглядного анализа. Поэтому в аэродинамике летательных аппаратов вводятся различные упрощающие приёмы и предположения. Очень часто оказывается целесообразным разделить полное движение самолёта на продольное и боковое. Продольным называется движение с нулевым креном, когда вектор силы тяжести и вектор скорости самолёта лежат в его плоскости симметрии. Далее будем рассматривать только продольное движение самолёта (рис. 1).
Это рассмотрение будем вести с использованием связанной ОXYZи полусвязанной ОXeYeZe систем координат. За начало координат обеих систем принимается точка, в которой расположен центр тяжести самолета. Ось ОX связанной системы координат проводится параллельно хорде крыла и называется продольной осью самолета. Нормальная ось ОY перпендикулярна оси ОX и расположена в плоскости симметрии самолета. Ось ОZ перпендикулярна к осям ОX и ОY, а следовательно, и к плоскости симметрии самолета. Она называется поперечной осью самолета. Ось ОXeполусвязанной системы координат лежит в плоскости симметрии самолета и направлена по проекции на неё вектора скорости. Ось ОYeперпендикулярна оси ОXe и расположена в плоскости симметрии самолета. Ось ОZe перпендикулярна к осям ОXe и ОYe.

Остальные обозначения, принятые на рис. 1: ![]() – угол атаки,
– угол атаки, ![]() – угол тангажа,
– угол тангажа, ![]() – угол наклона траектории,
– угол наклона траектории, ![]() – вектор воздушной скорости,
– вектор воздушной скорости, ![]() – подъемная сила,
– подъемная сила, ![]() – сила тяги двигателей,
– сила тяги двигателей, ![]() – сила лобового сопротивления,
– сила лобового сопротивления, ![]() – сила тяжести,
– сила тяжести, ![]() – угол отклонения рулей высоты,
– угол отклонения рулей высоты, ![]() – момент тангажа, вращающий самолёт вокруг оси ОZ.
– момент тангажа, вращающий самолёт вокруг оси ОZ.
Запишем уравнение продольного движения центра масс самолёта
![]() , (1)
, (1)
где ![]() – суммарный вектор внешних сил. Представим вектор скорости с использованием его модуля V и угла его поворота
– суммарный вектор внешних сил. Представим вектор скорости с использованием его модуля V и угла его поворота ![]() относительно горизонта:
относительно горизонта:
![]() .
.
Тогда производная вектора скорости по времени запишется в виде:
![]() . (2)
. (2)
С учётом этого уравнения продольного движения центра масс самолёта в полусвязанной системе координат (в проекциях на оси ОXe и ОYe) примут вид:
![]() ; (3)
; (3)
![]() . (4)
. (4)
Уравнение вращения самолёта вокруг связанной оси OZимеет вид:
![]() , (5)
, (5)
где Jz – момент инерции самолета относительно оси OZ, Mz – суммарный вращающий момент относительно оси OZ.
Полученные уравнения полностью описывают продольное движение самолета. В курсовой работе рассматривается только угловое движение самолёта, поэтому далее будем учитывать только уравнения (4) и (5).
В соответствии с рис. 1, имеем:
![]() , (6)
, (6)
где
![]() – (7)
– (7)
угловая скорость вращения самолёта вокруг поперечной оси OZ(угловая скорость тангажа).
При оценке качества управляемости самолета большое значение имеет перегрузка. Она определяется как отношение действующей на самолёт суммарной силы (без учёта веса) к силе веса самолёта. В продольном движении самолёта используют понятие «нормальная перегрузка». По ГОСТ 20058–80 она определяется как отношение проекции главного вектора системы сил, действующих на самолёт, без учёта инерционных и гравитационных сил, на ось OY связанной системы координат к произведению массы самолёта на ускорение свободного падения:
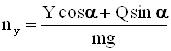 . (8)
. (8)
Переходные процессы по перегрузке и угловой скорости тангажа определяют оценку летчиком качества управляемости продольного движения самолета.
1.3 Силы и моменты при продольном движенииСилы и моменты, действующие на самолёт, – это сложные нелинейные функции, зависящие от режима полёта и положения управляющих органов. Так, подъёмная сила Y и сила лобового сопротивления Q записываются в виде:
![]() ; (9)
; (9)
![]() . (10)
. (10)
Суммарный момент ![]() есть функция скорости V и высоты H полёта, угла атаки
есть функция скорости V и высоты H полёта, угла атаки ![]() и скорости его изменения
и скорости его изменения ![]() , угловой скорости изменения угла тангажа (скорости вращения
, угловой скорости изменения угла тангажа (скорости вращения ![]() самолёта вокруг связанной поперечной оси OZ) и угла отклонения руля высоты
самолёта вокруг связанной поперечной оси OZ) и угла отклонения руля высоты ![]() :
:
![]() . (11)
. (11)
Здесь
сx, cy, ![]() – задаваемые табличным путём функции,
– задаваемые табличным путём функции,
![]() – плотность атмосферы,
– плотность атмосферы,
S – сечение Миделя (площадь характерного сечения самолёта).
Эти зависимости определяются специалистами по аэродинамике расчётным путём и уточняются с помощью продувок в аэродинамических трубах и путём натурного эксперимента.
1.4 Линеаризованные уравнения движения
Уравнения динамики продольного движения самолета существенно упрощаются при рассмотрении малых отклонений от горизонтального полета самолета с постоянной скоростью. Проведём линеаризацию уравнений углового продольного движения самолёта. Будем полагать, что за время переходных процессов по углам и угловым скоростям тяга двигателей P, модуль скорости V и высота полёта H остаются неизменными. Из выражений (5) и (11) получим:
![]() (12)
(12)
Из выражений (3) и (9) получим:
![]() (13)
(13)
Момент или сила с верхним индексом означают здесь соответствующую частную производную. Обозначим:
![]() ;
; ![]() (14)
(14)
Оказывается, что параметры ![]() и
и ![]() являются чрезвычайно информативными с точки зрения оценки режима полёта и качества угловых процессов самолёта. Пренебрежём, как это часто делается для маневренных самолётов, слагаемым
являются чрезвычайно информативными с точки зрения оценки режима полёта и качества угловых процессов самолёта. Пренебрежём, как это часто делается для маневренных самолётов, слагаемым ![]() в правой части уравнения (13). С учётом равенства (6) получим уравнение для производной приращения угла атаки:
в правой части уравнения (13). С учётом равенства (6) получим уравнение для производной приращения угла атаки:
![]() (15)
(15)
Уравнения (12) и (15) являются линейными дифференциальными уравнениями углового движения самолета в отклонениях.
Рассмотрим подробнее выражение (8) для нормальной перегрузки. При неизменном во времени модуле скорости V можно полагать, что сила тяги P примерно равна силе лобового сопротивления Q. Тогда
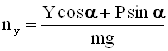 (16)
(16)
Теперь перейдём к приращениям:
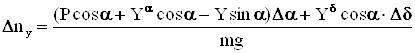 (17)
(17)
Тогда, полагая ![]() и пренебрегая величиной
и пренебрегая величиной ![]() , с учётом (14) для углов, измеряемых не в радианах, а в градусах, получим:
, с учётом (14) для углов, измеряемых не в радианах, а в градусах, получим:
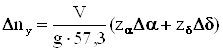 . (18)
. (18)
В предыдущих выражениях g – ускорение свободного падения, m – масса самолета. При численных расчетах полагаем ![]() м/с2.
м/с2.
Из (13) и (14), пренебрегая величиной ![]() , получим формулу для приращения ускорения самолёта по оси подъёмной силы:
, получим формулу для приращения ускорения самолёта по оси подъёмной силы:
![]() . (19)
. (19)
Учитывая (16), получим связь между приращениями нормальной перегрузки и ускорением
![]() . (20)
. (20)
Таким образом, о величине приращения нормальной перегрузки можно судить по показаниям датчика нормального ускорения (акселерометра).
Примем в качестве переменных состояния приращения угла атаки и угловой скорости тангажа. Заменив в правой части уравнения (12) ![]() выражением (15), получим следующие уравнения состояния:
выражением (15), получим следующие уравнения состояния:
![]() , (21)
, (21)
![]() , (22)
, (22)
где угловые величины выражены в градусах, а скорость – м/с.
В таблице приведены числовые данные для коэффициентов линеаризованных уравнений самолета для различных высот и скоростей полета. Вместо воздушной скорости полета V в таблице данных используется относительная скорость
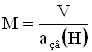 , (23)
, (23)
где величину M называют числом Маха, ![]() – скорость звука на данной высоте.
– скорость звука на данной высоте.
Схема электрогидравлического привода руля высоты представлена на рис. 2. Привод представляет собой следящую систему, входной величиной которой является электрический управляющий сигнал, а выходной – перемещение рабочего органа, связанного со стабилизатором (рулём высоты).
На сравнивающее устройство 2 подаются управляющий сигнал 1 и сигнал обратной связи 3, полученный с датчика обратной связи 16. Сигнал рассогласования 4 подаётся на вход электромеханического преобразователя 5. Собственно гидравлический усилитель, составляющий основу привода, является двухкаскадным. Питание первого каскада усиления осуществляется через редуктор 6. Заслонка 7, укрытая защитным колпачком 8, жёстко связана с якорем электромеханического преобразователя. При перемещении заслонки изменяются гидравлические сопротивления сопел 9, через которые непрерывно течёт рабочая жидкость под воздействием небольшого управляющего давления Pу. Переменные сопротивления сопел и постоянные гидравлические сопротивления дросселей 10 образуют гидравлический мост, диагональ которого составляет нагрузка – золотник 11. Поэтому при отклонении заслонки от среднего положения в областях А и Б золотника 11 образуется перепад давлений, создающий движущую силу. Пружины 12 выполняют роль жёсткой механической отрицательной обратной связи. Поршни золотника при постоянном положении заслонки 7 будут перемещаться до тех пор, пока сила пружины не уравновесит движущую силу. Таким образом, перемещение штока золотника пропорционально сигналу рассогласования 4. Смещение штока золотника совместно с закреплёнными на нём поршеньками приоткрывает соответствующий канал для передачи давления источника рабочей жидкости Рб на соответствующую сторону поршня силового цилиндра 13. Стрелками на рисунке показана подача рабочей жидкости высокого давления. В результате шток 14 силового цилиндра перемещается и через кинематическую передачу поворачивает руль высоты 15.
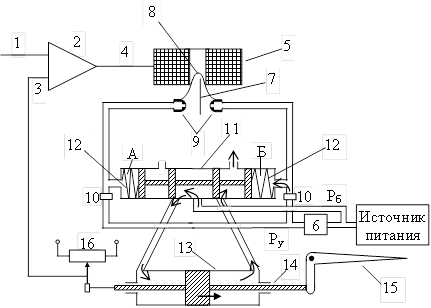
Рис. 2. Схема привода
Структурная схема электрогидравлического привода представлена на рис. 3.
Для пояснения способа получения структурной схемы обратимся к рис. 4, на котором изображено простейшее гидравлическое устройство. В камеру гидравлического устройства поступает жидкость, расход которой регулируется клапаном. (Под расходом жидкости понимается изменение её объема в единицу времени).
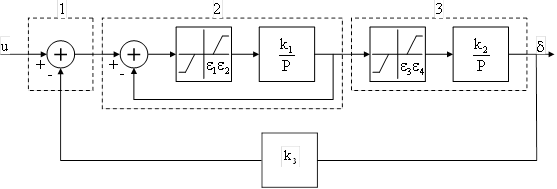
Рис. 3. Структурная схема электрогидравлического привода.
На рис. 3 приняты следующие обозначения: 1 – сравнивающее устройство; 2 – золотник; 3 – силовой механизм.
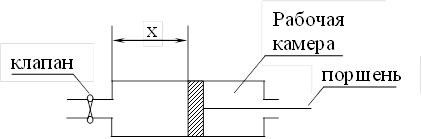
Рис. 4. Гидравлическое устройство
Если полагать, что расход жидкости пропорционален перемещению клапана r, то изменение объема жидкости в рабочей камере также пропорционально величине r. Поэтому скорость перемещения поршня пропорциональна величине r, т.е.
![]() , (24)
, (24)
где k – коэффициент пропорциональности.
Передаточная функция от величины r к x равна, очевидно, ![]() .
.
Нелинейные звенья вводятся для учета сил трения поршня о стенки рабочей камеры золотника и рабочего механизма (начальный участок нелинейной характеристики) и для учета ограничений величин максимальных расходов жидкости (конечный участок нелинейных характеристик).
Для расчетов предлагаются следующие величины числовых данных: ![]() ,
, ![]() ,
, 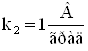 ,
, ![]()
![]()
![]()
![]() угол наклона нелинейных характеристик равен 450.
угол наклона нелинейных характеристик равен 450.
Максимальные углы отклонения стабилизатора составляют ±300 и достигаются в установившемся режиме при величине входного напряжения ±30В.
1.6 Математические модели датчиков угловой скорости и перегрузки
Приборы, предназначенные для получения сигналов, пропорциональных угловой скорости самолёта, так называемые датчики угловых скоростей (ДУС), обычно выполняются в виде гироскопа с двумя степенями свободы. С помощью указанных приборов вводится производная в закон регулирования. При этом гироскопические измерители угловой скорости обычно располагают на самолёте таким образом, что оси гироскопа оказываются параллельными соответствующим осям самолёта.
На рис. 5 приведена схема прибора (демпфирующего гироскопа), предназначенного для измерения угловой скорости тангажа.
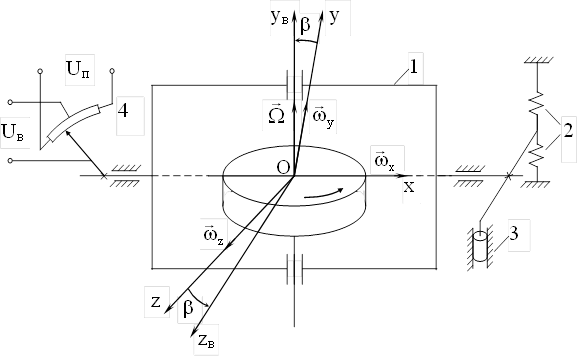 Рис. 5. Упрощенная схема демпфирующего гироскопа: 1 – двухстепенной гироскоп; 2 – пружина; 3 – демпфер; 4 – потенциометрический датчик.
Рис. 5. Упрощенная схема демпфирующего гироскопа: 1 – двухстепенной гироскоп; 2 – пружина; 3 – демпфер; 4 – потенциометрический датчик.
Ротор гироскопа вращается вокруг оси ![]() с большой угловой скоростью
с большой угловой скоростью ![]() . в этом случае ротор гироскопа обладает большим кинетическим моментом
. в этом случае ротор гироскопа обладает большим кинетическим моментом ![]() , где
, где ![]() – момент инерции ротора гироскопа относительно оси
– момент инерции ротора гироскопа относительно оси ![]() . Пусть Jx– момент инерции гироскопа вместе с рамкой относительно оси Ox. Тогда уравнение моментов относительно оси Ox имеет следующий вид:
. Пусть Jx– момент инерции гироскопа вместе с рамкой относительно оси Ox. Тогда уравнение моментов относительно оси Ox имеет следующий вид:
![]() *), (25)
*), (25)
где первое слагаемое в правой части равенства представляет собой гироскопический момент, Мп – момент пружины, Мд – момент демпфера. Проектируя это уравнение на ось Ox и полагая, что
![]() , (26)
, (26)
![]() , (27)
, (27)
где ![]() – жесткость пружины, f – коэффициент демпфирования, получим
– жесткость пружины, f – коэффициент демпфирования, получим
![]() . (28)
. (28)
Полагая величину ![]() малой, пренебрегая величиной
малой, пренебрегая величиной ![]() по сравнению с
по сравнению с ![]() , поскольку величина скорости вращения гироскопа велика, и введя обозначения
, поскольку величина скорости вращения гироскопа велика, и введя обозначения
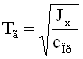 ,
, 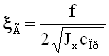 ,
,  , (29)
, (29)
получим дифференциальное уравнение второго порядка
![]() . (30)
. (30)
Поскольку электрический сигнал с выхода потенциометрического датчика пропорционален углу ![]() , то окончательно получим следующее выражение передаточной функции демпфирующего гироскопа:
, то окончательно получим следующее выражение передаточной функции демпфирующего гироскопа:
 . (31)
. (31)
Значения параметров передаточной функции 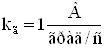 ,
, ![]() с,
с, ![]() .
.
Для измерения нормальной перегрузки используем осевой акселерометр. Схема осевого акселерометра представлена на рис. 6.
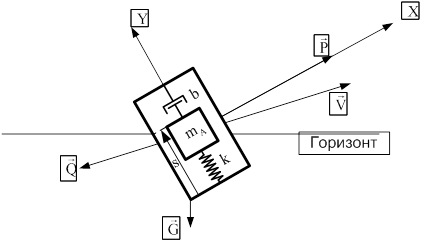
Рис. 6. Схема осевого акселерометра
Акселерометр, иначе называемый датчиком линейных ускорений (ДЛУ), во избежание зависимостей его показаний от угловых скоростей самолёта, устанавливается в центр тяжести самолёта. Его принципиальную схему можно представить в виде винтовой пружины k, один конец которой скреплен с корпусом прибора, а другой с массой ![]() , имеющей возможность перемещаться в направляющих, параллельных оси пружины. Эти направляющие определяют ось чувствительности прибора.
, имеющей возможность перемещаться в направляющих, параллельных оси пружины. Эти направляющие определяют ось чувствительности прибора.
Если самолёт, несущий ДЛУ, движется с ускорением, причём по оси чувствительности ДЛУ направлена составляющая ![]() этого ускорения, то сумма сил, действующих на массу
этого ускорения, то сумма сил, действующих на массу ![]() , равна
, равна
![]() , (32)
, (32)
или
![]() .*) (33)
.*) (33)
Здесь ![]() - жёсткость пружины,
- жёсткость пружины, ![]() - коэффициент успокоительного демпфера. Изменение положения подвижной массы акселерометра
- коэффициент успокоительного демпфера. Изменение положения подвижной массы акселерометра ![]() фиксируется потенциометрическим или индукционным линейным датчиком. Таким образом, передаточная функция акселерометра, определяемая как отношение изображений по Лапласу электрического выходного сигнала акселерометра к нормальному ускорению самолёта при нулевых начальных условиях, записывается следующим образом:
фиксируется потенциометрическим или индукционным линейным датчиком. Таким образом, передаточная функция акселерометра, определяемая как отношение изображений по Лапласу электрического выходного сигнала акселерометра к нормальному ускорению самолёта при нулевых начальных условиях, записывается следующим образом:
 . (34)
. (34)
Значения параметров передаточной функции осевого акселерометра ![]() с,
с, ![]() ,
, ![]() В/ед.
В/ед.
1.7 Математическая модель датчика положения штурвала
Схема включения датчика положения штурвала летчика представлена на рис. 7. На схеме обозначены:
1 – штурвал;
2 – загрузочные пружины;
3 – потенциометрический датчик положения ручки.
Управлять самолетом, не ощущая усилий на ручке, ориентируясь только по ее положению, чрезвычайно трудно. Поэтому искусственно создают имитирующее усилие на штурвале управления с помощью загрузочных пружин.
Сигнал с выхода потенциометрического датчика пропорционален отклонению штурвала летчика. Для численных расчетов полагаем величину коэффициента пропорциональности между перемещением штурвала и выходным напряжением датчика равной 0,1 В/мм. Максимальные величины отклонения штурвала составляют ± 100 мм.
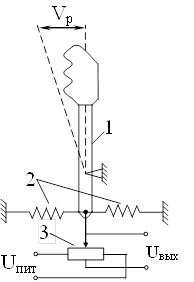
Рис. 7. Упрощенная схема штурвала летчика
Похожие работы
... году появились несколько патентов различные РЛС УВД. 1. G01S9/56 342-37 920616 Том 1139 №3 Способ и устройство для системы воспроизведения информации наземной РЛС. Система управления воздушным движением /УВД/ содержит РЛС обнаружения, радиомаяк и общий цифровой кодер для сопровождения самолетов и устранения возможности столкновений. В процессе передачи данных на систему УВД производится ...
... курсовой работы являются результаты курсовой работы по Аэродинамике «Расчёт аэродинамических характеристик самолёта Ан-124», его геометрические параметры, аэродинамические характеристики и крейсерские поляры. Курсовая работа содержит расчеты, графики и рисунки, пояснения и обоснования расчета летно-технических характеристик, характеристик продольной устойчивости и управляемости самолета. 1. ...
... средств является неприемлемой, т.к. жёсткая конкуренция на рынке транспортных услуг требует сокращения времени технического обслуживания до минимума. Скорость и надёжность проверки, во многом зависит от «человеческого фактора». Поэтому проверка функционирования системы улучшения устойчивости самолёта является довольно длительным, трудоёмким процессом, что приводит к лишним затратам труда и ...
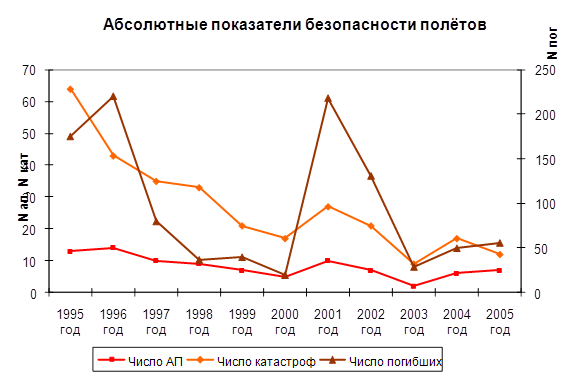
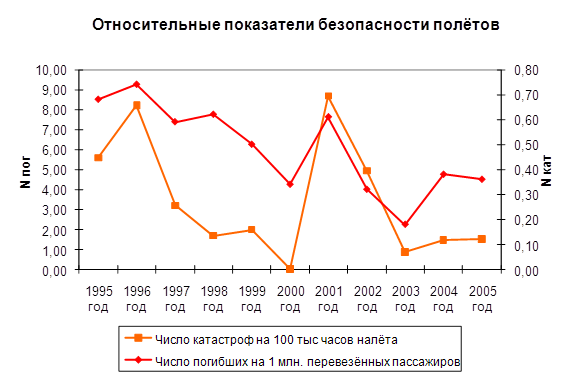
... " кат. Ка-32 RA-31007 22.10.05 3/2 Распределение авиационных происшествий в 2005 году по территориальным УГАН и подконтрольным им эксплуатантам показывает, что наиболее неблагоприятное положение с обеспечением безопасности полетов сложилось в Дальневосточном, Приобском, и Саха (Якутском) УГАН. Отмечаются серьезные недостатки в обеспечении безопасности полетов в Западно-Сибирском УГАН, где ...
0 комментариев