Навигация
Переходные и свободные колебания
12938
знаков
2
таблицы
17
изображений
Академия России
Кафедра Физики
ПЕРЕХОДНЫЕ И СВОБОДНЫЕ КОЛЕБАНИЯ В ЦЕПЯХ С ОДНИМ РЕАКТИВНЫМ ЭЛЕМЕНТОМ ПРИ СТУПЕНЧАТОМ ВОЗДЕЙСТВИИ
Орел 2009Содержание
Вступление
Переходные колебания в цепи с емкостью
Переходные колебания в цепи с индуктивностью
Методика нахождения реакций
Свободные колебания в электрической цепи
Библиографический списокВСТУПЛЕНИЕ
В данной лекции будет показан принцип применения операторного метода для анализа переходных колебаний в электрических цепях, содержащих один реактивный элемент и резисторы.
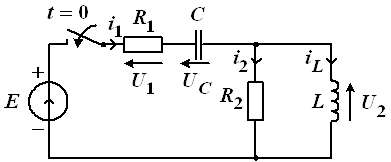
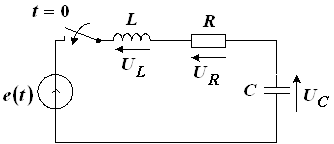
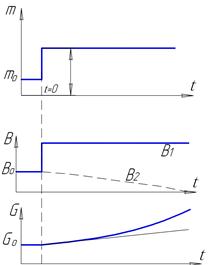
Будем считать, что на электрическую цепь, содержащую один реактивный элемент и резисторы, в момент 
действует ступенчатое воздействие в виде перепада постоянного тока или постоянного напряжения, условное обозначение которых показано на рисунке 1. Цепь находится при нулевых начальных условиях (НУ).
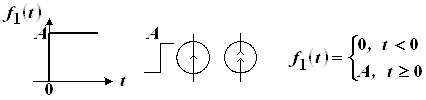
Рис. 1
В результате изучения материала курсанты должны уметь находить математическое выражение и строить график любой реакции на ступенчатое воздействие в цепях, содержащих один реактивный элемент и один или несколько резисторов.
Переходные колебания в цепи с емкостью
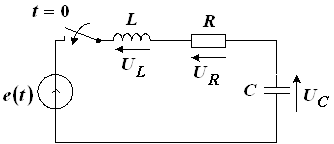
Рассмотрим воздействие перепада напряжения на последовательную RC-цепь. Пусть на последовательную RC-цепь, находящуюся при нулевых НУ в момент 
воздействует перепад напряжения 
(рис. 2).
Рис. 2
Найдем законы изменения тока в цепи 
и напряжений на ее элементах 
и 
.
На основании 2 закона коммутации: 
.
Для анализа переходного процесса используем операторный метод, для чего перейдем к операторной схеме замещения RC-цепи (рис. 3)
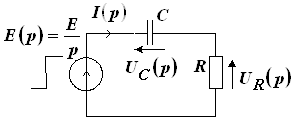
Рис. 3
Изображение тока в цепи определяется по закону Ома в операторной форме:
.
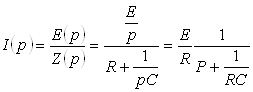По таблице соответствий найдем оригинал:
,
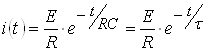где 
есть постоянная времени цепи.
Постоянная времени τ - промежуток времени, в течение которого напряжение (ток), убывая по экспоненциальному закону, уменьшается в е раз по отношению к значению напряжения (тока) в начале анализируемого промежутка времени. Она зависит от параметров цепи и влияет на крутизну экспоненты.
Напряжение на резисторе определяется по закону Ома для оригинала:
.
Закон изменения напряжения на емкости проще всего найти по 2‑ому закону Кирхгофа для оригиналов:
.
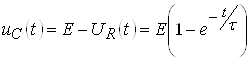Отметим, что при 
, 
, т. е. в момент перепада напряжения конденсатор представляет собой КЗ.
Графики данных функций описываются экспоненциальным законом и отличаются лишь начальным значением реакций. Их можно построить, составив таблицу значений 
для 
и 
для :
|
| 0 |
|
|
|
|
|
|
| 1 | 0,368 | 0,135 | 0,05 | 0,01 | <0,01 |
|
| 0 | 0,632 | 0,865 | 0,95 | 0,99 | >0,99 |
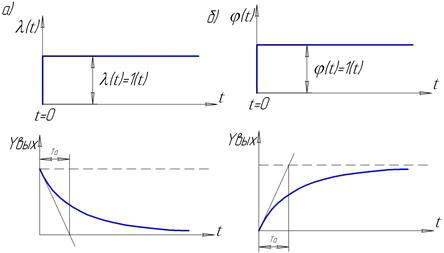
На рисунке 4 показаны графики и и их деформация при изменении 
цепи.
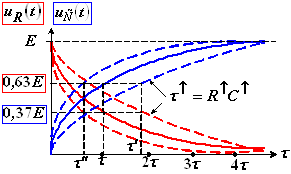
Рис. 4
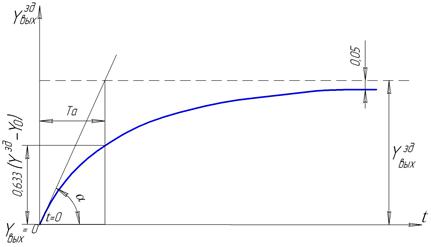
Постоянную времени цепи τ можно определить по следующему отношению величин, взятых из графика (рис. 4).
.
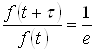Постоянная времени τ зависит от параметров цепи (R и С) и влияет на крутизну экспоненты (рис. 4):
- при уменьшении τ экспонента проходит круче и процесс переходных колебаний ускоряется;
- при увеличении τ, наоборот, экспонента проходит положе и процесс переходных колебаний замедляется.
Из графика видно, что теоретически переходные колебания в RC-цепи продолжаются бесконечно долго: f(t) → 0 (Е) при t → ∞.
Если рассмотреть промежуток времени t = 3τ, то окажется, что значение исходной функции уменьшается до 0,05 (увеличивается до 0,95) от начального значения, а при t = 4,6τ значение функции будет составлять всего 0,01 (0,99) от первоначального. Принято считать промежуток времени от t = 0 до t = (3
4,6)τ длительностью процесса переходных колебаний или временем установления.
Таким образом, tУСТ = (34,6)τ.
Примечание: постоянная времени сложной цепи определяется по той же формуле τ = RC, где R = RЭКВ – эквивалентное сопротивление, подключенное к элементу емкости после совершения коммутации, т. е. при t = +0. Это сопротивление находится, как в обычной резистивной цепи.
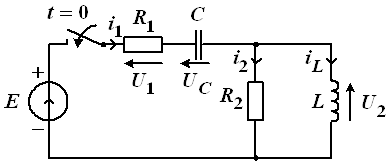
Соответствующая операторная схема показана на рисунке 6.
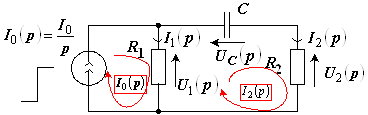
Рис. 6
Воспользуемся методом контурных токов:
;
;
.
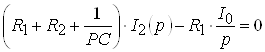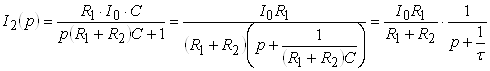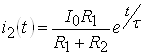Далее находим остальные реакции по первому закону Кирхгофа:
.
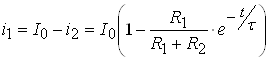Графики этих реакций, при 
, будут иметь вид (рис. 7):
Рис. 7
Напряжения на резисторах легко определяются путем умножения токов 
и 
на соответствующие сопротивления, а напряжение на емкости можно найти по второму закону Кирхгофа:
.
График данной функции имеет такой же вид, как и на рисунке 4.
Выводы:
Похожие работы
... коэффициента затухания и его соотношения с поскольку последним определяется величина . Поэтому в зависимости от и различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру. Режимы переходных колебаний в колебательных контурах Ранее было получено выражение для напряжения на контуре при ступенчатом воздействии: , где . Для удобства изложения ...
... метода применимы только для линейных электрических цепей, поскольку в их основе лежит метод наложения (суперпозиции). Сущность классического метода анализа переходных колебаний в электрических цепях Переходные процессы в электрических цепях описываются уравнениями, составленными на основании законов Кирхгофа для мгновенных значений напряжений и токов. Эти уравнения для различных цепей после ...
... сопротивление) механически из схемы не исключается. Отметим, что ступенчатое воздействие является простейшей функцией. Нахождение реакции на такое воздействие является одной из важных задач в теории переходных процессов (аналогично задаче нахождения реакции цепи на гармоническое воздействие в стационарном режиме). в) другие воздействия, например, в виде импульсов различной формы, включение и ...
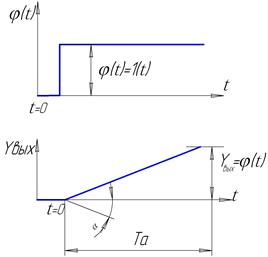
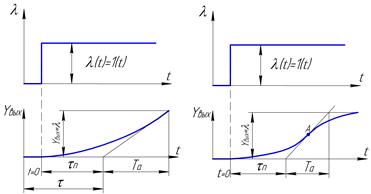
... – объекты, в которых регулируется расход жидкости или газа. Методы графического определения времени разгона Та для многоемкостных ОР приведены на рис. 5 и 6. Импульсные характеристики объектов регулирования Длительное и значительное по величине воздействие, которое приходится наносить для получения разгонных характеристик объекта регулирования, вызывает длительные изменение режима его работы ...
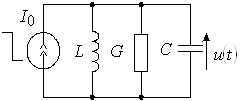
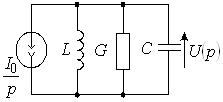
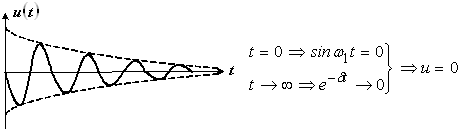
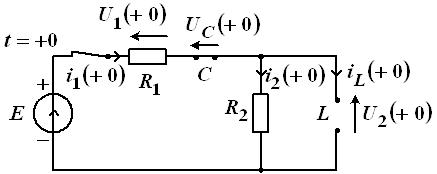
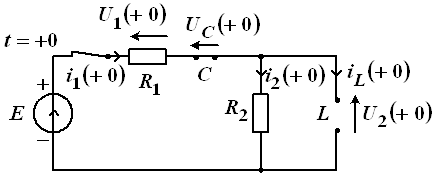
0 комментариев