Навигация
Свободные переходные процессы в цепи с индуктивностью
4.2. Свободные переходные процессы в цепи с индуктивностью
Пусть через индуктивность L протекает ток I0, т. е. при ![]() ,
, ![]() . В момент времени
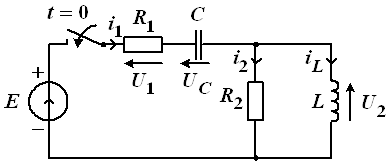
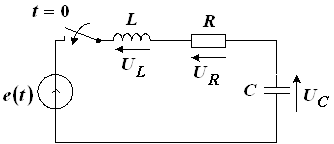
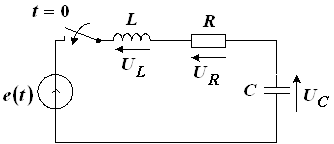
. В момент времени ![]() происходит коммутация – гасится источник (рис. 14).
происходит коммутация – гасится источник (рис. 14).
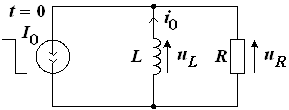
Рис. 14
За счет энергии, запасенной индуктивностью, происходит процесс свободных колебаний, пока вся энергия не израсходуется на нагрев резистора R. Найдем временные зависимости тока в цепи и напряжений на элементах R и L, которые, как видно из рисунка 14, одинаковы.
На основании 1-го закона коммутации ток через индуктивность не может измениться скачком, т. е. ![]() , и в момент времени
, и в момент времени ![]() ,
, ![]() , то есть начальные условия ненулевые.
, то есть начальные условия ненулевые.
Рассматриваемая схема для момента времени ![]() , т. е. сразу же после коммутации, имеет вид, показанный на рисунке 15, при этом индуктивность можно рассматривать как источник задающего тока.
, т. е. сразу же после коммутации, имеет вид, показанный на рисунке 15, при этом индуктивность можно рассматривать как источник задающего тока.
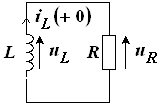
Рис. 15
Для нахождения закона изменения тока в цепи и напряжений на элементах R и L воспользуемся операторным методом, для чего индуктивность с током заменим одной из эквивалентных схем замещения. Здесь удобнее использовать параллельную схему замещения, при этом ток операторного источника тока соответствует начальному току через индуктивность. На рисунке 16 схема замещения индуктивности с током выделена пунктиром.
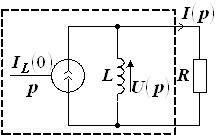
Рис. 16
На основании правила деления токов:
 .
.
Задача в операторной форме решена – получено выражение для преобразованного тока в цепи. На основании таблицы соответствий получим оригинал – временную зависимость тока в режиме свободных колебаний:
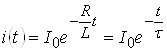 ,
,
где τ = ![]() – постоянная времени цепи, имеющая размерность [с].
– постоянная времени цепи, имеющая размерность [с].
Так как uL = uR, то их временные зависимости также одинаковы. По закону Ома для оригиналов:
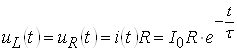 .
.
Таким образом, в цепи с индуктивностью в режиме свободных колебаний ток и напряжение на элементах R и L будут изменяться (как и в цепи с емкостью) по экспоненциальному закону с постоянной времени τ = ![]() . Физический смысл τ такой же, как и в цепи с емкостью. Постоянная времени зависит от параметров цепи R и L и влияет на крутизну экспоненты:
. Физический смысл τ такой же, как и в цепи с емкостью. Постоянная времени зависит от параметров цепи R и L и влияет на крутизну экспоненты:
- при увеличении τ, что достигается уменьшением величины R или увеличением величины L, экспонента проходит положе – процесс затухания свободных колебаний замедляется;
- при уменьшении τ, что достигается увеличением величины R или уменьшением L, экспонента проходит круче, и процесс затухания свободных колебаний ускоряется.
При этом ![]() , то есть скачок тока невозможен, а
, то есть скачок тока невозможен, а ![]() , то есть наблюдается скачок напряжения.
, то есть наблюдается скачок напряжения.
Тогда 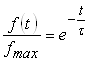 .
.
Этот график представляет собой убывающую экспоненту. Крутизна убывания определяется величиной постоянной времени τ. Вид графика не отличается от ранее рассмотренного для цепи с емкостью.
Время окончания свободных колебаний зависит от постоянной времени цепи и определяется так же, как и для цепи с емкостью:
tУСТ = (3![]() 4,6)τ.
4,6)τ.
Примечание: Постоянная времени сложной цепи определяется по формуле, τ =![]() , где R = RЭ – эквивалентное сопротивление, подключенное к элементу индуктивности после совершения коммутации, то есть при
, где R = RЭ – эквивалентное сопротивление, подключенное к элементу индуктивности после совершения коммутации, то есть при ![]() . Это сопротивление находится как в обычной резистивной цепи.
. Это сопротивление находится как в обычной резистивной цепи.
В результате анализа свободных колебаний в цепи с одним реактивным элементом можно сделать общие выводы.
1. Реакция (ток, напряжение) цепи на ступенчатое воздействие, формируется путем отключения от цепи источника энергии, представляет собой экспоненциальную убывающую функцию вида:
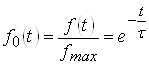 .
.
Это соответствует физическому смыслу: при отключении источника накопленная энергия убывает, она расходуется на нагрев активного сопротивления.
При анализе свободных колебаний необходимо определить начальное значение реакции, используя законы коммутации, начальные условия, постоянную времени цепи.
2. Закон изменения реакций справедлив и для сложных цепей, содержащих один реактивный элемент и несколько резисторов.
Библиографический список
1. Белецкий А. Ф. ТЛЭЦ: учебник для вузов. – М.: Радио и связь, 1986.
2. Шалашов Г. В. Переходные процессы в электрических цепях.
3. Бакалов В. П. ТЭЦ: учебник для вузов. – М.: Радио и связь, 1998
Похожие работы
... коэффициента затухания и его соотношения с поскольку последним определяется величина . Поэтому в зависимости от и различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру. Режимы переходных колебаний в колебательных контурах Ранее было получено выражение для напряжения на контуре при ступенчатом воздействии: , где . Для удобства изложения ...
... метода применимы только для линейных электрических цепей, поскольку в их основе лежит метод наложения (суперпозиции). Сущность классического метода анализа переходных колебаний в электрических цепях Переходные процессы в электрических цепях описываются уравнениями, составленными на основании законов Кирхгофа для мгновенных значений напряжений и токов. Эти уравнения для различных цепей после ...
... сопротивление) механически из схемы не исключается. Отметим, что ступенчатое воздействие является простейшей функцией. Нахождение реакции на такое воздействие является одной из важных задач в теории переходных процессов (аналогично задаче нахождения реакции цепи на гармоническое воздействие в стационарном режиме). в) другие воздействия, например, в виде импульсов различной формы, включение и ...
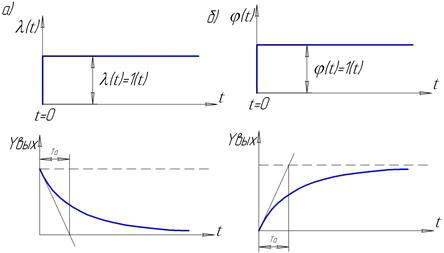
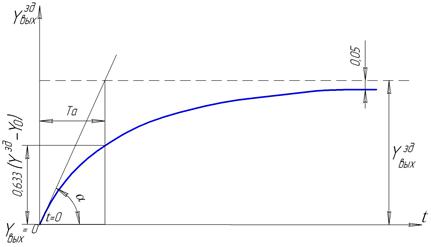
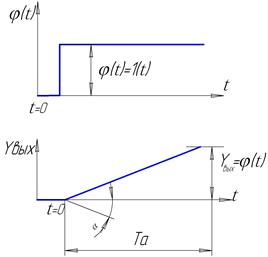
... – объекты, в которых регулируется расход жидкости или газа. Методы графического определения времени разгона Та для многоемкостных ОР приведены на рис. 5 и 6. Импульсные характеристики объектов регулирования Длительное и значительное по величине воздействие, которое приходится наносить для получения разгонных характеристик объекта регулирования, вызывает длительные изменение режима его работы ...


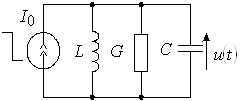
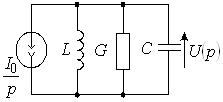
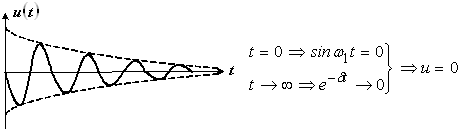
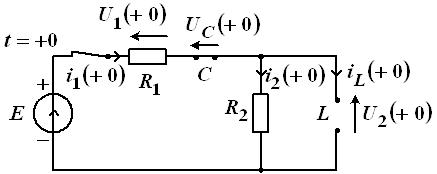
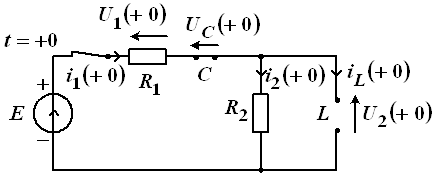
0 комментариев