Расчет режима

2.2 Расчет режима

Периодический несинусоидальный режим в линейных цепях возникает в одном из двух случаев:

1) в схеме есть источники энергии различной частоты, причём частоты кратны некоторому общему числу;

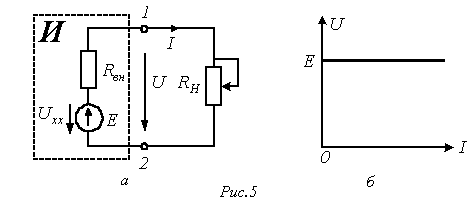
2) в цепи действуют источники энергии не синусоидальной формы, но с кратными периодами. Задачи этого типа легко сводятся к задаче первого типа, если каждый источник разложить в ряд Фурье, тогда схема замещения несинусоидального источника ЭДС:

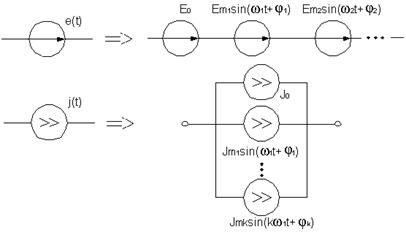
Задача первого типа легко решается методом наложения, т.к. цепь линейная. После расчёта всех частичных режимов ответ записывают как сумму мгновенных значений каждого режима, а уже затем ищут то, что требуется.

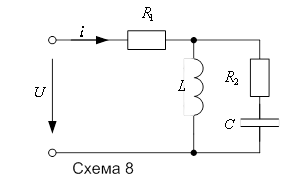
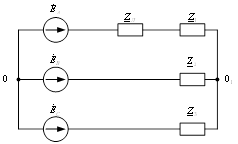
Пример:

, ,

1)

,

, .

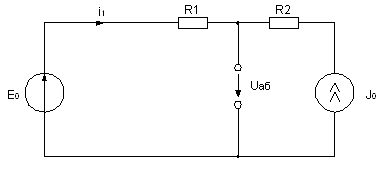
2) расчет на первой гармонике

, , ,

,

,

3) ,

Опять приходится рассчитывать сопротивление элементов, т.к. в каждом частичном режиме своя частота и получается, что сопротивление реактивных элементов зависят от номера гармоники.

,

,

,

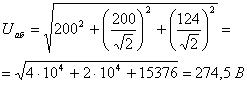
Как видно из расчёта при  входное сопротивление относительно зажимов ЭДС чисто активное, т. е. на этой гармонике наблюдается резонанс.

Вообще под резонансом в цепи с несинусоидальным режимом понимают резонанс на какой-то k-ой гармонике, т.к. в целом при несинусоидальном режиме понятие фазы неприменимо. На k-ой гармонике определение резонанса звучит как обычно. Другим важным примером из расчёта является то, что в разных участках цепи соотношение между гармониками различно, из-за того, что сопротивления реактивных элементов зависят от номера гармоники. Это широко используется для построения электрических фильтров.

2.3 Мощности в цепи несинусоидального тока

Различают:

1) мгновенная мощность: ,

2) полная мощность: ,

3) активная мощность: ,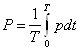

4) реактивная мощность: .

Способ расчёта потребляемой и генерируемой мощности такой же как и всегда.

Если u(t) и i(t) представлены в виде рядов Фурье: , , то можно упростить вычисление активной мощности.

Перемножим записанные ряды; получим три вида слагаемых:

1) ;

2)

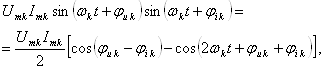
где k одно и то же;

3) произведение гармоник с разными номерами.

При интегрировании за период Т – каждое слагаемое третьего типа даёт ноль. Интеграл от слагаемого второго типа будет давать т.к. интеграл от  за период равен нулю. Слагаемое первого типа даст .

В результате получим, что

т.е. фактически активная мощность периодического несинусоидального тока равна сумме активных мощностей всех гармоник, начиная с нулевой.

, ,

, .

По аналогии вводится реактивная мощность, только вместо cos будет sin, и не будет учитываться нулевая гармоника:

.

Заключение

На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.

На практике к несинусоидальности напряжений и токов следует подходить двояко:

- в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов;

- в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями.

Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами.

В заключение следует отметить, что методика расчета линейных цепей при несинусоидальных токах сводится к следующему:

Ø  ЭДС и токи источников раскладываются в ряды Фурье.

Ø  Осуществляется расчет цепи в отдельности для каждой гармонической.

Ø  Искомые величины определяются как алгебраические суммы соответствующих гармонических.

Список литературы

1. Основы теории цепей. Учебник для вузов./ Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов.-5-е изд. перераб.-М.: Энергоатомиздат, 1989. 528 с.

2. В.П. Попов. Основы теории цепей. Учебник для вузов. -М.: Высшая школа, 1985. 496 с.

3. Л.А. Бессонов. Теоретические основы электротехники. Электрические цепи. Изд. 10. Учебник для вузов.- М.: Гардаргики, 2002. 638 с.

4. Теория электрических цепей: Методические указания к лабораторным работам / Рязан. гос. радиотехн. акад.; Сост.: С.М. Милюков, В.П. Рынин; Под ред. В.П. Рынина. Рязань, 2002. 16 с.,2004. 20 с. (№3282, №3624)

5. Электротехника и электроника: Методические указания к расчетно-графической работе / Рязан. гос. радиотехн. акад.; Сост. Г.В. Спивакова. Рязань, 2005. 16 с. (№3665)

6. Основы теории цепей: Методические указания к курсовой работе / Рязан. гос. радиотехн. акад.; Сост.: В.Н. Зуб, С.М. Милюков. Рязань, 2005. 16 с.

7. Теоретические основы электротехники. / Г.И. Атабеков, С.Д. Купалян, А.В. Тимофеев, С.С. Хухриков. - М.: Энергия, 1979. 424 с.

8. М.Р. Шебес. Теория линейных электрических цепей в упражнениях и задачах. М.: Высшая школа, 1990. 528 с.

9. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

10. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

11. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М. Поливанова. Т.1. К.М. Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.