Навигация
Бросаются две игральные кости. Найти для произведения очков на выпавших гранях: математическое ожидание; дисперсию
4448
знаков
1
таблица
0
изображений
5. Бросаются две игральные кости. Найти для произведения очков на выпавших гранях: математическое ожидание; дисперсию
Решение. Введем независимые случайные величины 
и 
равные, соответственно, числу очков, выпавших на первой и на второй кости. Они имеют одинаковые распределения:
|
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Найдем математическое ожидание
.
Найдем дисперсию
.
Тогда математическое ожидание 
суммы числа очков, которые могут выпасть при одном бросании двух игральных костей равно
.
Дисперсия суммы числа очков, которые могут выпасть при одном бросании двух игральных костей равна (так как бросания костей независимы):
.
Ответ: 7; 35/6.
6. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 30 и 4. Найти вероятность того, что Х в 5 испытаниях ровно 3 раза примет значение, заключенное в интервале (29, 31)
Решение. Используем формулу
,
где математическое ожидание
, среднее квадратическое отклонение 
α=29, β=31.
P(29<х<31)=Ф(
=Ф(0,25)-(0,25)= Ф(0,25)+Ф(0,25) = 2∙Ф(0,25) = 2∙0,3413∙0,25 = 0,17065 Ответ: 0,17065
7. В порядке серийной выборки из 1000 контейнеров бесповторным отбором взято 10 контейнеров. Каждый контейнер содержит равное количество однотипных изделий, полученных высокоточным производством. Межсерийная дисперсия проверяемого параметра изделия равна 0,01. Найти: границы, в которых с вероятностью 0,99 заключено среднее значение проверяемого параметра во всей партии, если отобрано 50 контейнеров, а общая средняя равна 5
При беспроводном отборе применяется формула:
n= 
N=1000 n=
=5 
p=0,99 
≈0,98
Подставим:
5=
5=
5000
+0,049=98
0,049=98
Т.к. х=5, то интервал 5
0,14
Похожие работы
... получаем, что с доверительной вероятностью р=0,997: а для р=0,95 которые называются доверительными интервалами для теоретической средней М. Ясно, что если доверительные интервалы для М из двух групп не пересекаются, то нулевую гипотезу следует отвергнуть. Например, опросили еще одну группу из N =9 человек и получили следующее число правильных ответов: шкала xi 6 7 8 9 10 11 12 13 ...
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
... же для нахождения энергетически оптимальной концентрации эритроцитов в крови, парциального давления в артериальной и венозной крови, определения оптимальных функциональных параметров системы внешнего дыхания и др. 2 Принцип минимального воздействия в эколого-математических моделях Один из способов применения целевой функции состоит в формулировании общего утверждения относительно поведения ...
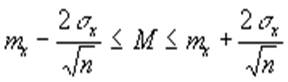
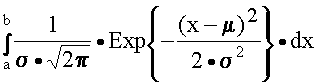
0 комментариев