Министерство образования Российской Федерации
Институт дистанционного образования
ГОУ ВПО « Тюменский государственный университет »
Контрольная работа
по дисциплине: «Высшая математика»
Тема: «ДВОИНЫЕ ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА»
УК (220501.65)/3. сокращенная
Выполнил студент Петренко Н. В.
Нижневартовск 2010
Контрольная работа
Вариант 5
1. Вычислить интегралы:
1.1. 
где D – прямоугольник 
1.2. 
где D – область, ограниченная линиями 
2. Найти общее решение уравнений:
2.1. 
2.2. 
Решение контрольной работы.
1. где D – прямоугольник
Построим область D:
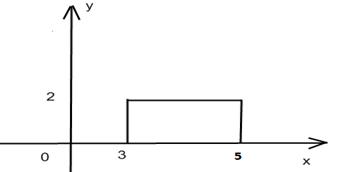
Сводя двойной интеграл к повторному и расставляя пределы, получаем:
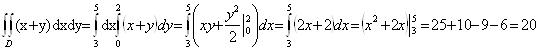
Ответ: I=20.
2. где D – область, ограниченная линиями
Построим область D, которая ограничена ветвью гиперболы у=6/х, расположенной в первой четверти и прямой у=7-х. Находим точки пересечения: 6/х=7-х; 
, откуда х=1 и х=6. Имеем две точки (1;6) и (6;1).
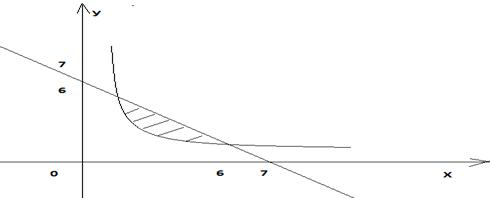
Запишем границы области D: 
Сводя двойной интеграл к повторному и расставляя пределы, получаем:
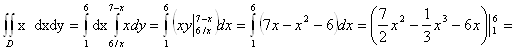
=126-72-36-7/2+1/3+6=24-19/6=(144-19)/6=125/6.
Ответ: I=125/6.
3.
Характеристическое уравнение 
имеет кратные корни k=2, поэтому общее решение имеет вид: 
.
Ответ: .
4.
Это линейное неоднородное дифференциальное уравнение (ЛНДУ). Решением ЛНДУ является сумма решений соответствующего однородного (ЛОДУ) и любого частного решения. Решаем ДУ: у''+y'-2=0. Характеристическое уравнение 
имеет корни k =-2 и k=1, поэтому общее решение однородного ДУ имеет вид: 
. Частное решение будем искать в виде: 
. Дважды дифференцируем последнее: 
. Подставляем в заданное ДУ и приравниваем коэффициенты:
, откуда В=-3, С=-3, D=-4,5. Запишем общее решение заданного неоднородного ДУ: 
.
Ответ: .
Похожие работы
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... плотность тока вероятности .(1.9) Из (1.9) следует, что j = 0 для всех функций , у которых функция Ф не зависит от координат. В частности, j= 0 для всех действительных функций . Решения уравнения Шредингера (1.1) в общем случае изображаются комплексными функциями. Использование комплексных функций весьма удобно, хотя и не необходимо. Вместо одной комплексной функции состояние системы можно ...
... масса свариваемого металла изменяется несущественно удобно в расчетах использовать удельную объемную теплоемкость, численно равную произведению массовой теплоемкости на плотность. Дифференциальное уравнение теплопроводности Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается так называемым дифференциальным уравнением теплопроводности, на основе ...
0 комментариев