Навигация
Надежность, эргономика и качество АСОИУ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАМСКАЯ ГОСУДАРСТВЕННАЯ
ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ»
Факультет «Автоматизации и прогрессивные технологии»
Кафедра «Прикладная информатика и управление»
Лабораторная работа №1
«Надежность, эргономика и качество АСОИУ»
Выполнила: ст. гр. 1325
Гайнутдинова А.И.
Проверил: Тазмеев А.Х.
Г.Набережные Челны
2010г.
«ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ЭЛЕМЕНТОВ ПО ОПЫТНЫМ ДАННЫМ»
1.1 Постановка задачи
Дано:
· N – число элементов, находящихся на испытании;
· ti – время исправной работы i -го элемента, i = 1, 2,..., п;
· п – число отказавших элементов за время испытания t.
Определить показатели надежности элемента:
· λ(t) – интенсивность отказа как функцию времени;
· f(t) – плотность распределения времени исправной работы элемента;
· ω (t) – параметр потока отказов как функцию времени.
Эти показатели надежности необходимо определить при следующих двух видах испытания:
а) с выбрасыванием отказавших элементов;
б) с заменой новыми или отремонтированными.
В случае (а) число элементов в процессе испытания убывает, в случае (б) — остается постоянным.
Варианты задания приведены далее в разд. 1.5.
1.2 Сведения из теории
В теории надежности под элементом понимают элемент, узел, блок, имеющий показатель надежности и входящий в состав системы. Элементы бывают двух видов: невосстанавливаемые (резистор, конденсатор, подшипники и т. п.), и восстанавливаемые или ремонтируемые (генератор тока, колесо автомобиля, телевизор, ЭВМ и т. п.). Отсюда следует, что показателями надежности невосстанавливаемых элементов являются только такие показатели, которые характеризуют надежность техники до ее первого отказа.
Показателями надежности восстанавливаемых элементов являются показатели, которые характеризуют надежность техники не только до первого отказа, но и между отказами.
Показателями надежности невосстанавливаемых элементов являются:
· P(t) – вероятность безотказной работы элемента в течение времени t;
· T1– среднее время безотказной работы (наработка до отказа);
· f(t) — плотность распределения времени до отказа;
· λ(t) — интенсивность отказа в момент t.
Между этими показателями существуют следующие зависимости:
![]() , (1.1)
, (1.1)
![]() ,
, 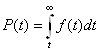 , (1.2)
, (1.2)
![]() , (1.3)
, (1.3)
![]() . (1.4)
. (1.4)
Интенсивность отказа многих элементов, особенно элементов электроники, является величиной постоянной: λ(t) = λ. В этом случае зависимости между показателями надежности имеют вид:
![]() ,
,
![]() ,
,
![]() .
.
Показателями надежности восстанавливаемых элементов являются:
· ω(t) – параметр потока отказов в момент времени t;
· T – среднее время работы между отказами (наработка на отказ).
Показателями надежности восстанавливаемых элементов могут быть также показатели надежности невосстанавливаемых элементов. Это имеет место в тех случаях, когда система, в состав которой входит элемент, является неремонтируемой по условиям ее работы (необитаемый космический аппарат, аппаратура, работающая в агрессивных средах, самолет в процессе полета, отсутствие запчастей для ремонта и т. п.). Между показателями надежности невосстанавливаемых и восстанавливаемых элементов имеют место следующие зависимости:
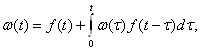 (1.5)
(1.5)
![]() (1.6)
(1.6)
Из выражений для показателей надежности невосстанавливаемых и восстанавливаемых элементов можно сделать следующий важный вывод: основным показателем надежности элементов сложных систем является интенсивность отказов λ(t). Это объясняется следующими обстоятельствами:
· надежность многих элементов можно оценить одним числом, т. к. их интенсивность отказа — величина постоянная;
· по известной интенсивности λ(t) наиболее просто оценить остальные показатели надежности элементов и сложных систем;
· λ(t) обладает хорошей наглядностью;
· интенсивность отказов нетрудно получить экспериментально.
Следует, однако, иметь в виду, что плотность распределения наиболее полно характеризует случайное явление — время до отказа. Остальные показатели, в том числе и λ(t), лишь в совокупности позволяют достаточно полно оценить надежность сложной системы.
Основным способом определения показателей надежности элементов сложных систем является обработка статистических данных об их отказах в процессе эксплуатации систем или при испытаниях в лабораторных условиях. При этом возможны следующие два случая:
· отказавшие элементы в процессе испытания или эксплуатации системы новыми не заменяются (испытания без восстановления);
· отказавший элемент заменяется новым того же типа (испытания с восстановлением).
В процессе эксплуатации системы или при испытаниях в лабораторных условиях фиксируется дата возникновения отказа. По этим данным путем статистической обработки и определяются показатели надежности элементов.
Как следует из определений показателей надежности невосстанавливаемого элемента, все они могут быть вычислены, если известен закон распределения времени работы элемента до отказа в виде плотности f(t). Если элемент может ремонтироваться, то все показатели надежности выражаются через закон распределения времени безотказной работы f(t). Поэтому важным обстоятельством является умение находить f(t) с помощью проведения и обработки результатов эксперимента.
Предположим, что в результате проведения испытаний над N элементами в течение времени Т получены некоторые статистические данные о распределении количества отказавших элементов. Возможны три способа регистрации отказов элементов.
· Первый способ регистрации
Элементы, поставленные на испытания, являются невосстанавливаемыми. При возникновении отказа некоторого элемента фиксируется момент времени его отказа.
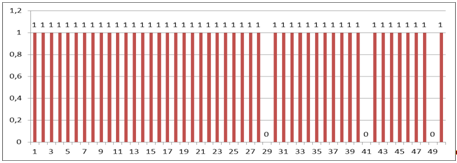
В результате испытаний статистической информацией является последовательность t1, t2,..., ti,..., tN моментов времени отказа элементов (рис. 1.1).
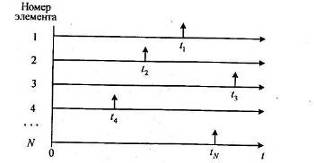
Рис. 1.1. Временная диаграмма моментов отказов невосстанавливаемых элементов
· Второй способ регистрации
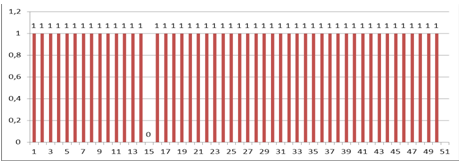
Элементы, поставленные на испытания, являются восстанавливаемыми. После отказа какого-либо элемента он заменяется новым. В результате испытаний исходной статистической информацией является последовательность моментов времени отказов i-го элемента ti,j (i = 1, 2,..., N и j = l, 2,...,ni) в течение периода наблюдений Т (рис. 1.2). Реализациями наработок элемента в этом случае служат разности τi, j = ti, j - ti, j-1 (предполагается, что ti,0 = 0).
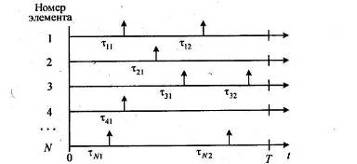
Рис. 1.2. Временная диаграмма моментов отказов восстанавливаемых элементов с известными номерами
Второй способ регистрации отказов, очевидно, сводится к первому, если фиксируются номера отказавших элементов. В качестве статистических данных берется совокупность разностей τi,j, представляющих собой времена работы элементов до первого отказа.
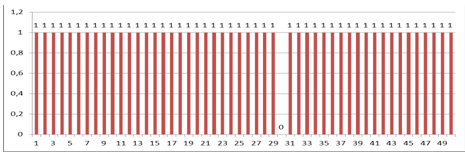
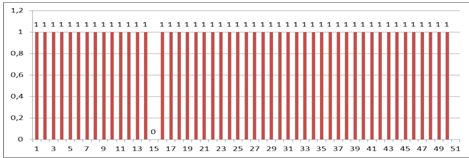
· Третий способ регистрации
Элементы, поставленные на испытания, являются восстанавливаемыми. После отказа какого-либо элемента он заменяется новым, однако не известен номер отказавшего элемента. В результате испытаний исходной статистической информацией является последовательность t1, ,t2,,… ,ti,...,tnмоментов отказов элементов, где п – число отказавших элементов. Таким образом, в отличие от второго способа, здесь регистрируются моменты отказов элементов без указания их номеров.
Рассмотрим статистические определения показателей надежности элемента. Соответствующий статистический аналог показателя надежности будем обозначать тем же символом, что и раньше, но со знаком (^) сверху.
Невосстанавливаемые элементы
Исходными статистическими данными является время работы элементов до первого отказа: t1, t2,..., ti,..., tN . Тогда среднее время работы элемента до отказа равно среднему арифметическому времени ti, т. е
![]()
Обозначим через v(t) число элементов, для которых отказ произошел позднее момента времени t. Тогда вероятность отказа элемента равна
![]()
а вероятность безотказной работы — ![]()
Пусть последовательность t(1), t(2),..., t(i), ...,t(N) получена упорядочением исходной последовательности. Функция ![]() представляет собой эмпирическую функцию распределения, и если все t(i) различны, то
представляет собой эмпирическую функцию распределения, и если все t(i) различны, то
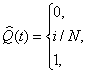 при t<t(1)
при t<t(1)
при t(1)≤t<t(i+1)
при t≥t(N)
Величина всех скачков равна 1/N, а типичный график функции ![]() приведен на рис. 1.3.
приведен на рис. 1.3.
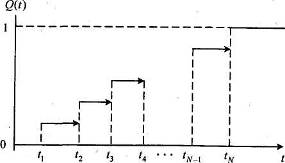
Рис. 1.3. График статистической вероятности отказа элемента
Другим наглядным способом представления статистических данных является гистограмма. Область значений [t(1); t(N)] разбивается на равные интервалы Δi = 1, 2,..., k, длины ![]() , где R = t(N)-t(1), и называется размахом выборки. Гистограмма представляет собой примыкающие друг к другу прямоугольники, основанием которых являются указанные интервалы, а высоты равны плотностям относительных частот
, где R = t(N)-t(1), и называется размахом выборки. Гистограмма представляет собой примыкающие друг к другу прямоугольники, основанием которых являются указанные интервалы, а высоты равны плотностям относительных частот ![]() , где Ni– число выборочных значений, попавших в данный интервал (рис. 1.4). Гистограмма является статистической плотностью распределения времени работы до отказа. Для оценки плотности иногда используется также полигон относительных частот, который представляет собой ломаную линию, построенную по точкам, абсциссами которых являются середины интервалов Δi = 1, 2,..., k, а ординаты соответствуют плотностям
, где Ni– число выборочных значений, попавших в данный интервал (рис. 1.4). Гистограмма является статистической плотностью распределения времени работы до отказа. Для оценки плотности иногда используется также полигон относительных частот, который представляет собой ломаную линию, построенную по точкам, абсциссами которых являются середины интервалов Δi = 1, 2,..., k, а ординаты соответствуют плотностям ![]() (рис. 1.4).
(рис. 1.4).
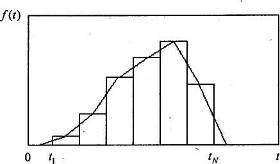
Рис. 1.4. График статистической плотности распределения в виде гистограммы и полигона частот
Интенсивность отказа элемента рассчитывается как отношение плотности распределения к вероятности безотказной работы.
Восстанавливаемые элементы
Исходными статистическими данными являются моменты времени отказов элементов: t1, t2,..., ti,..., tn, где п – число отказавших элементов, N – общее число элементов, участвующих в испытаниях. Информация об отказах элементов может быть представлена в виде табл. 1.1. Весь период испытаний разбивается на интервалы времени определенной длины, и подсчитывается количество отказавших элементов на каждом интервале.
Таблица 1.1. Таблица отказов элементов
| Δt | Δt1 | Δt2 | … | Δtk |
| Δn | Δn1 | Δn2 | … | Δn k |
Табличные данные означают, что на интервале времени Δti, было зафиксировано точно Δni, отказов элементов, i = 1, 2, ... ,k. Тогда имеет место следующее статистическое определение параметра потока отказов элемента:
![]()
Для всех t, принадлежащих i - интервалу времени:
![]() .
.
Определение плотности распределения f(t) путем решения интегрального уравнения (1.5) связано с некоторыми трудностями, которые вызваны скачкообразным изменением параметра потока отказов. Один из возможных подходов к определению функции f(t) состоит в следующем. Найдем функцию f(t) в виде кусочно-постоянной функции
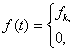 если ak-1< t ≤ak , k=1, 2, … , n;
если ak-1< t ≤ak , k=1, 2, … , n;
если t>an
Здесь a0 = 0, an= T, fk – искомые величины, которые можно определить из условия выполнения уравнения (1.5) в среднем по интегральной метрике
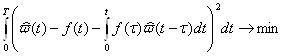
при ограничениях
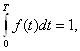
![]()
Вариант 3
Дано:
· Два набора исходных данных об отказах элементов.
· N – число элементов в каждом наборе.
· Закон распределения времени до отказа в первом варианте.
· Закон распределения времени между отказами во втором варианте.
· Моменты отказа элементов.
Определить:
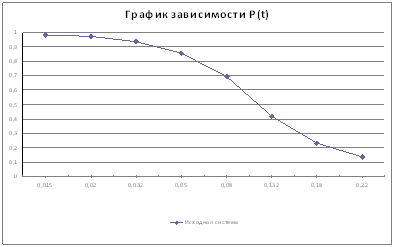
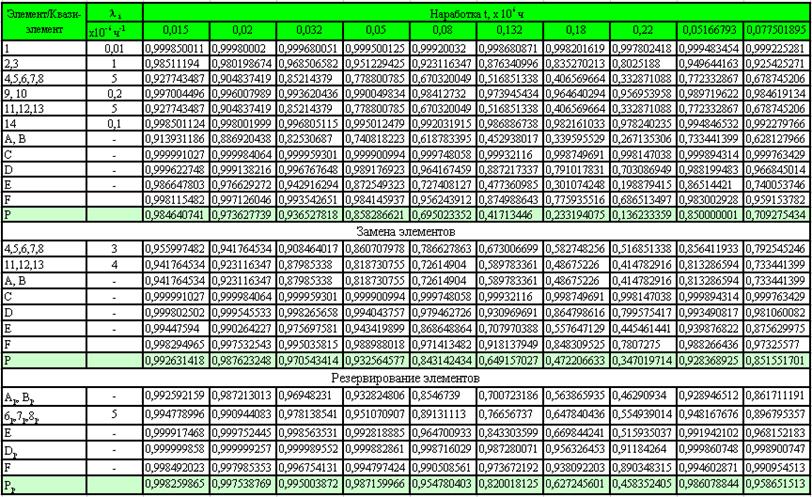
· Показатели надежности элемента, характеризующие время его работы до отказа (первый набор исходных данных): Т1, Р(t), Q(t), f(t), λ(t).
· Показатели надежности элемента, характеризующие время его работы между отказами (второй набор исходных данных): Т2, F(t), f(t), λ(t).
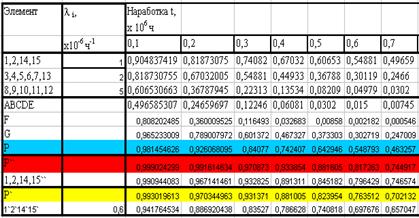
Решение получить в виде таблиц и графиков.
При обработке данных вручную и на компьютере их следует разобрать 10 групп (классов). Подбор подходящего распределения необходимо установить для уровня значимости, равного 0,05.
Обозначения:
Нормальное распределение – Normal Distribution;
Экспоненциальное распределение – Exponential Distribution;
Гамма-распределение – Gamma Distribution;
Равномерное распределение – Uniform Distribution;
Похожие работы
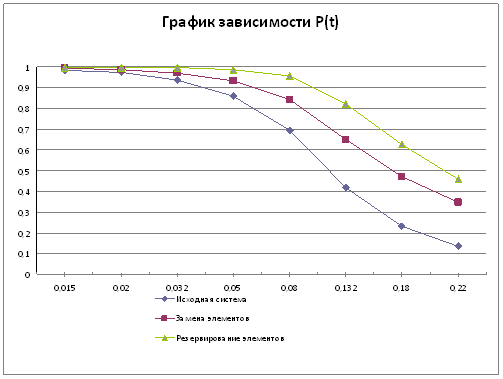
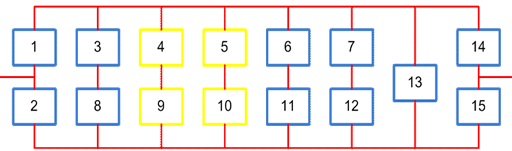
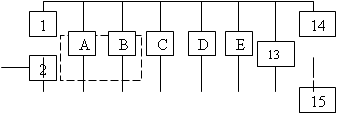
... до уровня 0,1-0,2 2) определить γ процентную наработку технической системы 3) обеспечить увеличение γ процентной наработки не менее чем в 1,5 раза за счет: а) повышения надежности элементов б) структурное резервирование элементов системы Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов), резервирование отдельных элементов или ...
... - процентную наработку технической системы. 3. Обеспечить увеличение - процентной наработки не менее, чем в 1.5 раза за счет: а) повышения надежности элементов; б) структурного резервирования элементов системы. Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по ...
... size: 0.8em; line-height: 150%; color: #000; } p.serif { font-family: Georgia, "Times New Roman", Times, serif; } </style> </head> <body> ТЕХНОЛОГИИ СОЗДАНИЯ ГИПЕРТЕКСТОВЫХ ДОКУМЕНТОВ Web-сайт - это большая и сложная система, основанная на тесном взаимодействии множества различных технологий. Клиентские средства разработки используются в основном для форматирования и ...
... директории и файлы, ролевая политика безопасности. 1.4 Цель дипломного проекта Целью дипломного проекта является разработка проекта и создание автоматизированной системы утверждения учебных планов и графиков учебных процессов, изучение структуры и принципов работы с документами в АГТУ, изучение технологии утверждения учебных планов и графиков учебного процесса, а также интегрирование в ...



0 комментариев