Навигация
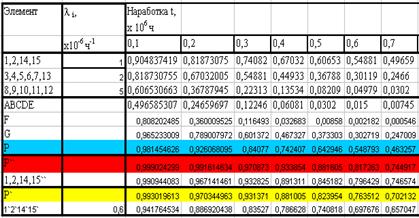
Определение статистических показателей для каждого набора данных, содержащихся в переменных OTKAZ.narabotka1 и OTKAZ.narabotka2
2. Определение статистических показателей для каждого набора данных, содержащихся в переменных OTKAZ.narabotka1 и OTKAZ.narabotka2.
Нажатием кнопки StatWizard ![]() получим:
получим:
Это приведет к расчету требуемых характеристики и выводу их на экран в следующем виде:
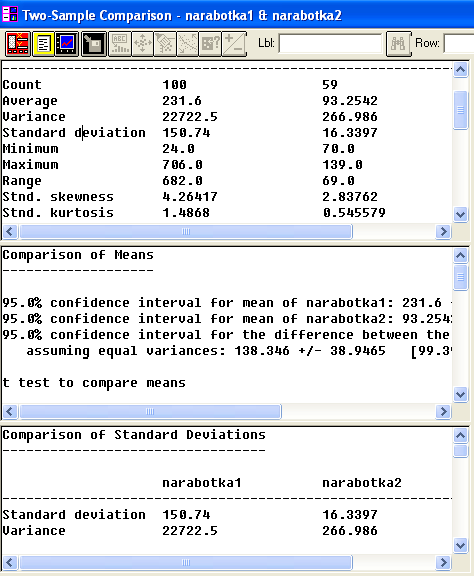
| Narabotka1 | Narabotka2 | |
| Размер выборки | 100 | 59 |
| Среднее значение | 231,6 | 93,2542 |
| Стандартное отклонение | 150,74 | 16,3397 |
| Минимум | 24,0 | 70,0 |
| Максимум | 706,0 | 139,0 |
| Размах | 682,0 | 69,0 |
Отсюда следует, что для первого набора исходных данных средняя наработка до первого отказа приближенно равна T1=362 часа, а для второго набора средняя наработка на отказ равна T2 = 95 часов. В первом случае распределение времени работы элемента между отказами явно отличается от экспоненциального, т. к. стандартное отклонение s1= 237 существенно отличается от средней наработки на отказ. Во втором случае стандартное отклонение s2 =91 достаточно близко к средней наработке до отказа, что свидетельствует о возможной близости распределения к экспоненциальному.
Видим также, что для первого набора данных все реализации случайной наработки до отказа находятся в интервале [30; 997], и размах выборки равен 967 часов. Для второго набора данных все выборочные значения содержатся в интервале [2; 371] длиной 369 часов.
Определение показателей надежности неремонтируемого элемента
Нажатием кнопки Capability Analysis ![]()
Заполним поля Data и USL. В Analysis Options контекстного меню выберем пункт Gamma получим гистограмму частот и выравнивающую ее функции плотности Гамма-распределения (рис. 1.5).
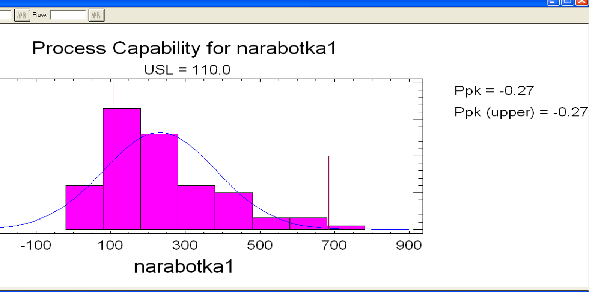
Рис. 1.5. Подбор плотности распределения к гистограмме частот
Значение Estimated Beyond Spec, равное 72,890636% указывает на уровень значимости для Гамма-распределения: 0,728906. Так как это значение больше требуемого 0,05, то Гамма-распределение согласуется с экспериментальными данными.
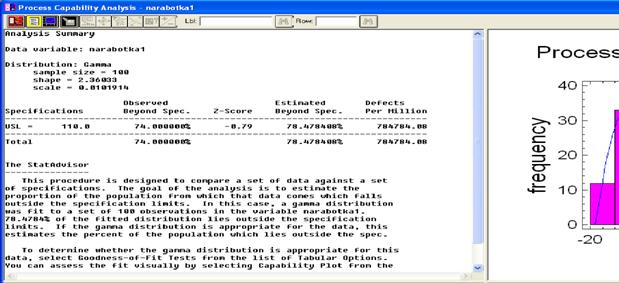
Значения Shape и Scale необходимо будет запомнить, так как они потребуются нам в дальнейшем.
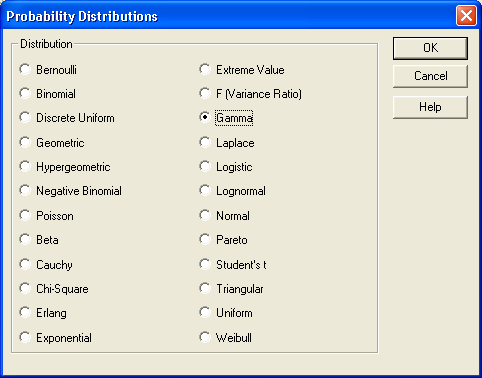
В пункте меню Describe\Distributions\Probability Distributions построим графики требуемых показателей надежности в соответствии с рассчитанными ранее параметрами.
Для переменной narabotka1 подберем Гамма-распределение. Выберем пункт Gamma.
В окне Probability Distributions раскроем вспомогательное меню Graphical Options и отметим соответствующие пункты:
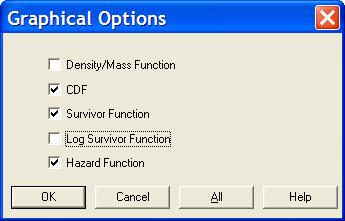
Пункты вспомогательного меню означают следующее:
Density function — плотность распределения f(t);
Cumulative d.f. — функция распределения Q(t);
Survivor function — вероятность безотказной работы P(t);
Log survivor function — логарифм вероятности безотказной работы;
Hazard function — интенсивность отказов λ(t).
В результате выбора того или иного пункта меню получим графики, изображенные на рис. 1.6—1.8.
В Analysis Options контекстного меню введем значение Shape и Scale.
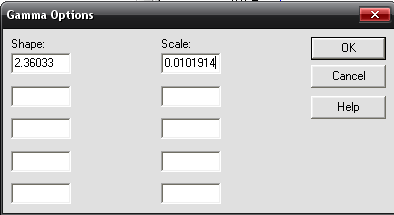
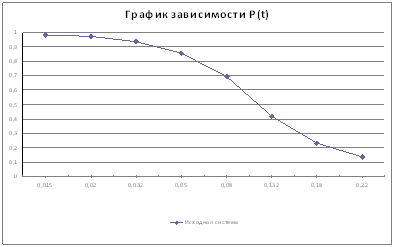
Рис. 1.6. Вероятность безотказной работы элемента P(t)
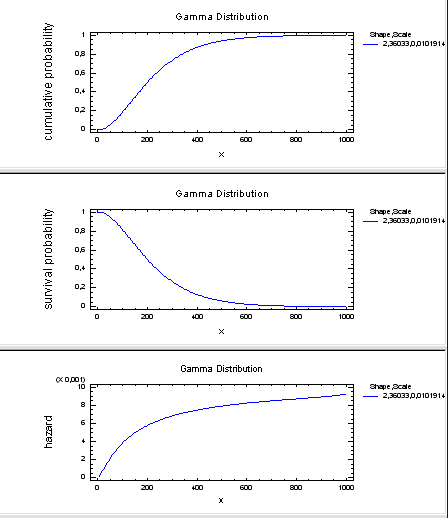
Рис. 1.7. Вероятность отказа элемента Q(t)
Рис. 1.8. Интенсивность отказов элемента λ(t)
Определение показателей надежности ремонтируемого элемента
Нажатием кнопки Capability Analysis ![]()
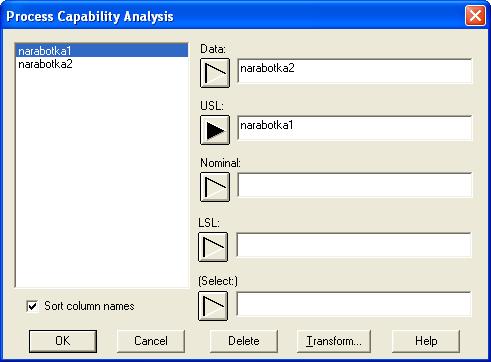
Заполним поля Data и USL. В Analysis Options контекстного меню выберем пункт Exponential, получим гистограмму частот и выравнивающую ее функции плотности экспоненциального распределения (рис. 1.5).
Гистограмма по narabotka2 и соответствующая кривая экспоненциального распределения приведены на рис. 1.9. Значение Estimated Beyond Spec, равное 28,449182% указывает на уровень значимости для экспоненциального распределения: 0,284492, что больше заданного уровня значимости, равного 0,05. Следовательно, экспоненциальное распределение не противоречит опытным данным.
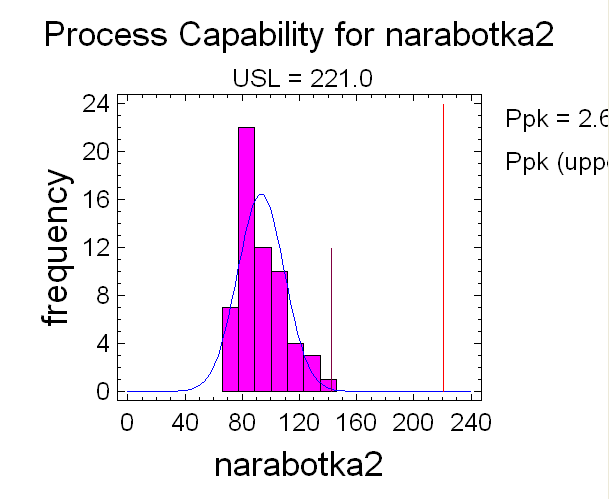
Рис. 1.9. Подбор плотности распределения w(t) к гистограмме частот
В пункте меню Describe\Distributions\Probability Distributions построим графики требуемых показателей надежности в соответствии с рассчитанными ранее параметрами.
Для переменной narabotka2 подберем Экспоненциальное распределение. Выберем пункт Exponential.
В окне Probability Distributions раскроем вспомогательное меню Graphical Options и отметим следующие пункты:
Cumulative d.f. — функция распределения Q(t);
Hazard function — интенсивность отказов λ(t).
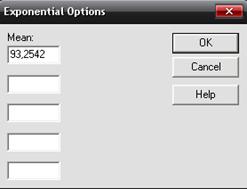
В пункт Analysis Options контекстного меню введем следующие параметры экспоненциального распределения: среднее отклонение = 93,2542
На рис. 1.10. и 1.11 изображены графики функций распределения и интенсивности отказов соответственно.
Средняя наработка на отказ равна T= 93,2542 час.
Рис. 1.10. Функция распределения времени работы элемента между отказами F(t)
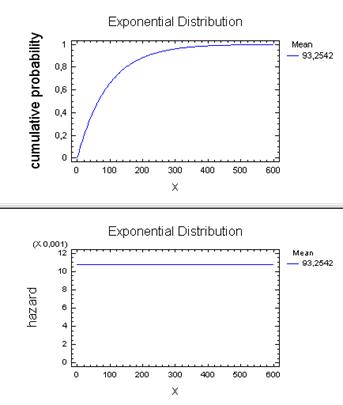
Рис. 1.11. Интенсивность отказов элемента λ(t) Обработка статистических данных
Размах варьирования:
![]()
Количество интервалов размаха варьирования:
Вопрос о выборе числа и ширины интервалов группировки приходится решать в каждом конкретном случае исходя из целей исследования, объема выборки и степени варьирования признака в выборке. Однако, приближенно число интервалов k можно оценить исходя только из объема выборки n. Делается это одним из следующих способов:
1) по формуле Стерджеса:
![]()
2) с помощью таблицы
Выбор числа интервалов группировки
| Объем выборки, n | Число интервалов, k |
| 25—40 | 5—6 |
| 40—60 | 6—8 |
| 60—100 | 7—10 |
| 100—200 | 8—12 |
| Больше 200 | 10—15 |
Разобьем размах варьирования на k интервалов:
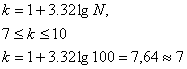 ,
,
где N-число элементов выборки. N=100.
k округляется в сторону ближайшего меньшего целого числа.
Длина интервала:
![]()
Количество отказов выборки, попавших в i-ый интервал(количество чисел, в данном интервале из таблицы 1):
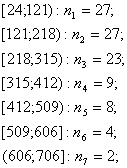
Не все интервалы удовлетворяют условию n>=5, следовательно, требуется объединение интервалов.
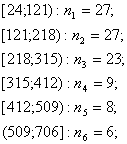
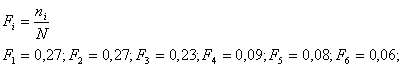
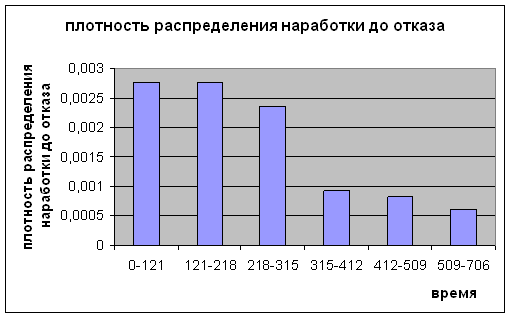
Плотность распределения наработки до отказа:
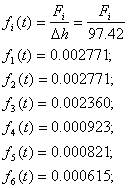
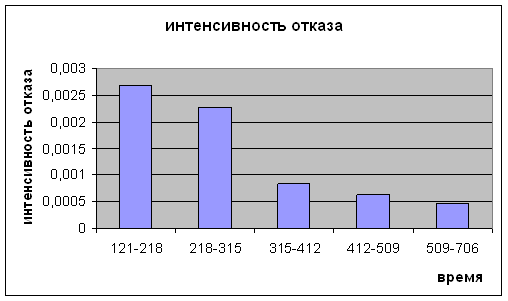
Интенсивность отказа в момент t:

Гистограммы:
Плотность распределения наработки до отказа в i-ом интервале:
Интенсивность отказа в i-ом интервале:
Похожие работы
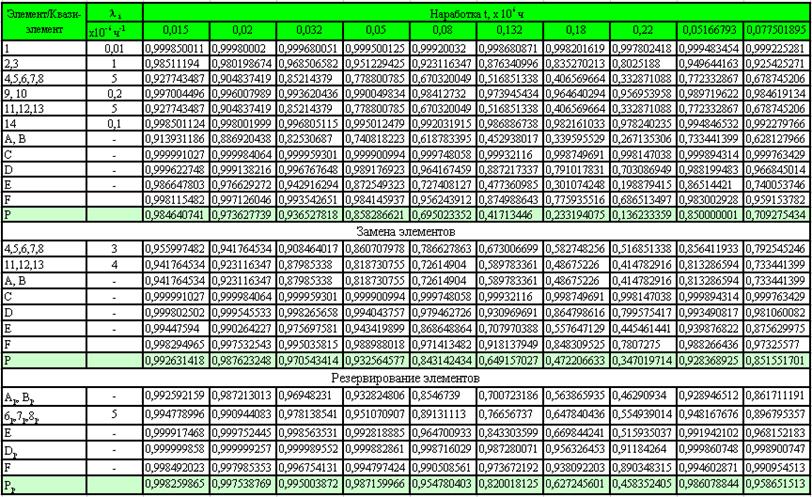
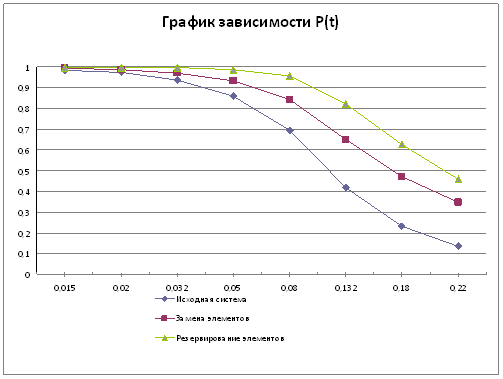
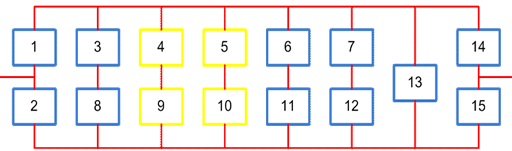
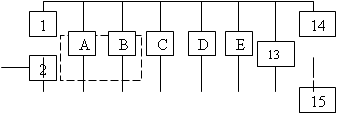
... до уровня 0,1-0,2 2) определить γ процентную наработку технической системы 3) обеспечить увеличение γ процентной наработки не менее чем в 1,5 раза за счет: а) повышения надежности элементов б) структурное резервирование элементов системы Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов), резервирование отдельных элементов или ...
... - процентную наработку технической системы. 3. Обеспечить увеличение - процентной наработки не менее, чем в 1.5 раза за счет: а) повышения надежности элементов; б) структурного резервирования элементов системы. Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по ...
... size: 0.8em; line-height: 150%; color: #000; } p.serif { font-family: Georgia, "Times New Roman", Times, serif; } </style> </head> <body> ТЕХНОЛОГИИ СОЗДАНИЯ ГИПЕРТЕКСТОВЫХ ДОКУМЕНТОВ Web-сайт - это большая и сложная система, основанная на тесном взаимодействии множества различных технологий. Клиентские средства разработки используются в основном для форматирования и ...
... директории и файлы, ролевая политика безопасности. 1.4 Цель дипломного проекта Целью дипломного проекта является разработка проекта и создание автоматизированной системы утверждения учебных планов и графиков учебных процессов, изучение структуры и принципов работы с документами в АГТУ, изучение технологии утверждения учебных планов и графиков учебного процесса, а также интегрирование в ...



0 комментариев