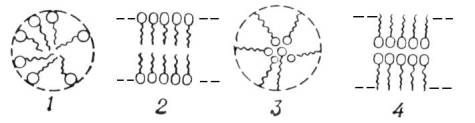
Пространственные – структуры характерны для дисперсных систем с анизодиаметрическими частицами;

1. Пространственные – структуры характерны для дисперсных систем с анизодиаметрическими частицами;

2. Компактные – структуры часто возникают в системах с изодиаметрическими частицами.

При истинной коагуляции, когда частицы полностью теряют фактор устойчивости, они слипаются друг с другом, образуя компонентные агрегаты. Достигнув определенного размера, эти агрегаты образуют плотный коагулят. Если же происходит неполная астабилизация системы, то фактор устойчивости будет снят только с некоторых участков поверхности частиц, да ито не полностью, и в результате этого частицы, слипаясь по таким местам, образуют пространственную сетку, в петлях которой находится дисперсная среда. Происходит гелеобразование.

Гелеобразованием называют переход коллоидного раствора из свободнодисперсного состояния (золя) в связомодисперсионное состояние (гель).

На гелеобразование влияет ряд факторов:

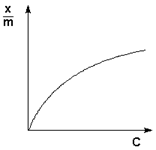
·  концентрация дисперсной среды;

·  уменьшение размера частиц;

·  температура;

·  механическое воздействие.

Аналогичный переход раствора ВМС в студень называется застудневанием. Оно может происходить спонтанно, в результате изменения температуры при концентрировании раствора или при добавлении к нему не слишком большого количества электролита.

Студни обладают такими свойствами как вязкость, осмотическое давление, эластичность, текучесть, особенность рассеивать свет, тиксотропные свойства, синтерезис.

Тиксотропия – способность структур после их разрушения в результате какого-нибудь механического воздействия самопроизвольно восстанавливаться во времени.

Синтерезис - самопроизвольное уменьшение размеров геля с одновременным выделением из него дисперсной среды, содержащейся в петлях геля.

Студни и процесс застудневания имеют большое значение в медицине, биологии, техники, хлебопекарной промышленности. Образование клеевого слоя при склеивании, желатировании пироксилина, получение искусственного волокна, дубление кожи.

2. Коагуляционные и конденсационно–кристаллизационные структуры по П.А. Ребиндеру

Согласно Ребиндеру, структуры в коллоидных и микрогетерогенных системах можно разделить на:

·  коагуляционные (тиксотропно-обратимые) – структуры, возникающие в результате понижения агрегативной устойчивости дисперсных систем, когда частицы полностью теряют фактор устойчивости, они слипаются друг с другом, образуя компактные агрегаты.

·  конденсационно-кристаллизационные (необратимые - разрушаюшиеся структуры) – связи между частицами образованы за счет химических сил. Эти структуры возникают либо в результате образования прочных химических связей между частицами, либо вследствие сращивания кристалликов в процессе выкристаллизовывания новой фазы.

3 Нормальные ньютоновские жидкости, структурированные жидкости. Вязкость. Аномалия вязкости. Уравнение Ньютона, Пуазейля, Бингама. Реологические зависимости. Уравнения Эйнштейна для определения вязкости коллоидных систем

Жидкообразные тела классифицируют на:

1. ньютоновские жидкости – системы, вязкость которых не зависит от напряжения сдвига и является постоянной величиной в соответствии с законом Ньютона;

2. структурированные – течение которых не следует закону Ньютона, их вязкость зависит от напряжения сдвига;

2.1 стационарные – реологические свойства которых не изменяются со временем;

2.2 нестационарные – для которых эти характеристики зависят от времени.

Вязкость – способность жидкого вещества оказывать сопротивление движению. В жидкостях вязкость обусловлена внутренним давлением и с повышением температуры вязкость понижается. В газах вязкость обусловлена тепловым движением молекул, с повышением температуры вязкость возрастает.

Коэффициент вязкости представляет собой силу сопротивления , которая возникает между слоями текучего тела с поверхностями площадью  и удаленными друг от друга на расстояние  при перемещении их относительно друг друга со скоростью .

 - динамическая вязкость

Свойства вещества, противоположные вязкости, называется текучестью, а величину противоположная коэффициенту вязкости коэффициент вязкости.

Кинематическая вязкость учитывает плотность вещества и связана с динамической вязкостью:

,

Жидкости способные течь, но не подчиняющиеся закону Ньютона, принято называть аномальными.

По определению вязкости, данному Ньютоном, сила внутреннего трения , равная по значению, но обратная по направлению приложенной извне силе, пропорциональная площади слоя , к которому приложена эта сила, и градиенту скорости движения между слоями:

,

Относя силу  к площади, тогда уравнение будет выглядеть так:

,

где  - напряжение сдвига, поддерживающее течение жидкости.

Ламинарное течение жидкости по трубкам описывается уравнением Пуазейля:

,

где  - объемная скорость истечения;

 - радиус и длина трубки;

 - разность давлений на концах трубки;

 - вязкость жидкости.

Бингам выразил пластическую вязкость уравнением:

,

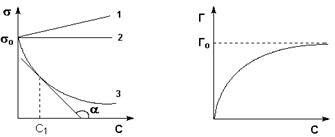
где  - угол, образуемый прямой с осью абцисс.

Однако для большинства структурированных коллоидных систем зависимость  от  выражается не прямой, а кривой.

Причина такого явления заключается в том, что при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения градиента скорости жидкости.

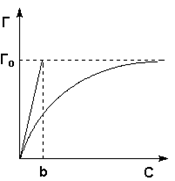
Различают три критических напряжения сдвига:

1.   - первый, или минимальный, предел текучести, соответствующий началу течения.

2.   - предел текучести по Бингаму, отвечающий отрезку на оси абсцисс, отсекаемому продолжением прямолинейного участка кривой.

3.   - максимальный предел текучести, соответствующий значению , при которой кривая переходит в прямую линию.

Первая аксиома реологии: при всестороннем равномерном сжатии материальные системы ведут себя одинаково – как идеальные упругие тела.

Вторая аксиома реологии: любая материальная система обладает всеми реологическими свойствами.

Эйнштейном была установлена связь между вязкостью дисперсной системы  и объемной долей дисперсной фазы :

,

где  - вязкость дисперсной среды.

Была установлено, что коэффициент при  зависит от формы частиц, поэтому уравнению Эйнштейна можно придать более общий вид:

,

где  - коэффициент, зависящий от формы частицы дисперсной фазы.

Для относительной и удельной вязкости дисперсной системы уравнение Эйнштейна переходит в следующие соотношения:

IV. Раздел «Растворы ВМС»

Похожие работы

Краткая история развития коллоидной химии как науки

Скачать

14177

0

0

... «мицелла» и «мицеллярный раствор». Эти термины были использованы им для обозначения систем, образованных нестехиометрическими соединениями в водной среде. Основная заслуга в становлении коллоидной химии как науки принадлежит Т. Грэму. Как уже отмечалось выше, именно этому ученому принадлежит идея введения термина «коллоид», производного от греческого слова «kolla», обозначающего «клей». Занимаясь ...

Коллоидная химия и поверхностные явления

Скачать

25685

1

9

... Расстояние, пройденное веществом по сорбенту, прямо пропорционально растворимости данного вещества в пропускаемом растворителе. Даёт возможность полностью разделять вещества, входящие в состав разделяемой смеси. Коллоидная химия Дисперсные системы – это системы, состоящие из множества частиц одной фазы (дисперсной), распределённых в объёме другой фазы – дисперсионной. Дисперсионная среда ...

Коллоидные системы в организме и их функции

Скачать

83726

2

5

... и многое другое, без чего немыслима сама жизнь. Все человеческое тело – это мир частиц, находящихся в постоянном движении строго по определенным правилам, подчиняющимся физиологии человека. Коллоидные системы организмов обладают рядом биологических свойств, характеризующих то или иное коллоидное состояние: 2.2 Коллоидная система клеток. С точки зрения коллоидно-химической физиологии ...

Подразделения химии

Скачать

6800

0

0

... металлов с белками, нуклеиновыми кислотами, липидами. Её практическое применение связано с синтезом фарамакологических препаратов, действие которых обусловленно комплексными ионами металлов. Биоорганическая Химия Изучает связь между строениями органических веществ и их биологическими функциями, использующих в основном методы органической и физической химии, а также физики и математики. ...