Определение математического ожидания

3.2  Определение математического ожидания

Оценка математического ожидания  как экспериментальное (выборочное) значение первого начального момента случайной величины X равна

,

В тоже время оценка среднего всей генеральной совокупности значений случайной величины определяется из выражения 

,  (9)

где - независимые случайные величины с одинаковыми, т.е. с числовыми характеристиками, равными истинным, но неизвестным априори, их значениям.

Математическое ожидание погрешности оценки среднего равно

.  (10)

Дисперсия погрешности оценки среднего равна

. (11)

Среднее квадратическое отклонение оценки математического ожидания

 .  (12)

Как видно из (10,11) оценка (9) – несмещенная, состоятельная и эффективная.

Выражения (8-12) могут быть положены в основу определения требуемого размера выборки для обеспечения заданных значений доверительного интервала погрешности и доверительной вероятности. Так, имея требования к величине доверительного интервала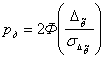  и доверительной вероятности  и принимая гипотезу о гауссовом характере распределения погрешности оценивания , т.е. возможности определения доверительной вероятности в виде , из выражения (8) определяем требуемое значение среднего квадратического отклонения погрешности оценки 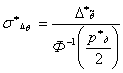. Вместе с тем из выражения (12) следует, что среднее квадратическое значение погрешности оценки среднего случайной величины связано со значениями СКО  и объемом выборки N следующей зависимостью:

,

откуда, приравнивая правые части последних равенств, окончательно определяем выражение для расчета требуемого объема выборки

.

Здесь значение СКО случайной величины может задаваться априорно, либо определяться экспериментально по выборке меньшего чем N объема.

Определение оценки дисперсии и ее среднего квадратического отклонения

Оценка дисперсии как экспериментальное значение второго центрального момента случайной величины X может быть вычислена по формуле

.

Так как значение априори неизвестно, то принимают и тогда

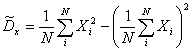.  (13)

Математическое ожидание погрешности оценки равно

,  (14)

 что означает, что оценка (14) является смещенной.

 Смещение пропорционально D_x и обратно пропорционально N. Это означает, что оценка D_x, полученная согласно (14), - состоятельная.

Смещение устраняется с переходом к .

При этом вместо (13) имеем

.  (15)

При больших значениях N результаты расчета по формулам (13) и (15) практически будут одинаковыми.

Выражение для дисперсии оценки (15), равной дисперсии погрешности , при нормальном виде закона распределения X (для худшего случая) можно получить следующее [1-3]:

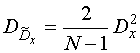.  (16)

Зависимость среднего квадратического отклонения от его точного значения определяется выражением

.

 

 

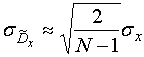3.3Определение корреляционного момента и коэффициента корреляции

Экспериментальное значение корреляционного момента R_xy как оценка смешанного центрального момента m₁₁ системы двух случайных величин равно

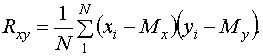
Так как значения М_х,  М_у неизвестны, то принимают ,  и тогда

ИЛИ

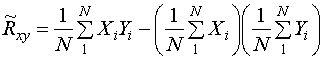.  (17)

Погрешность оценки

   (18)

Математическое ожидание погрешности (18)

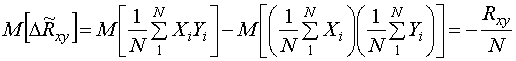
Это означает, что оценка (17) - смещена и равна

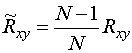.  (19)

Можно показать, что она является и состоятельной.

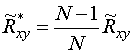Смещение устраняется с переходом от  к .  При

этом вместо (17) имеем

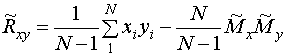. (20)

Для дисперсии оценки (17), равной дисперсии  погрешности (18), можно получить [1-3]

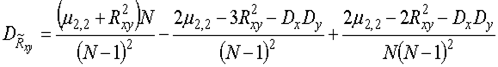, (21)

где  - четвертый смешанный центральный момент системы (X Y). При Y = X выражения (20) и (21) превращаются в (15), (16). Если система (X Y) распределена нормально, то  и согласно (21)

Так как значения R_xy, D_x, D_y неизвестны, то практически используется приближение

.  (22)

Среднее квадратическое значение погрешности (18) равно среднему квадратическому отклонению оценки (20):

. (23)

Оценка коэффициента корреляции определяется согласно

. (24)
Если оценки ,  получены в результате одной серии наблюдений, а оценка  – в результате другой, то их погрешности    ,  – независимые случайные величины, являющиеся аргументами линейной функции:

 . (25)

Значение  рассчитывается согласно (15), доверительный интервал  – по формуле (8).