Определение вероятности события

3.4 Определение вероятности события

Экспериментальное значение вероятности Р некоторого события - это частость [1-3]

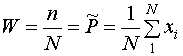,  (26)

причем число п появлений события в серии из N испытаний можно рассматривать как сумму N независимых случайных слагаемых:

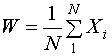,  (27)

каждое из которых может принимать только два значения 1 и 0 с вероятностями  P и 1 – P.

Математическое ожидание и дисперсия случайной величины X_i:

. (28)

Погрешность оценки (26) равна

.  (29)
Математическое ожидание погрешности и ее дисперсия:

.  (30)

Таким образом, оценка (26) - несмещенная и состоятельная. Среднее квадратическое отклонение оценки (26)

.

На практике принимают

.  (31)

3.5 Определение законов распределения случайной величины

Экспериментальное определение законов распределения случайных величин сводится к определению оценок вероятностей, математических ожиданий, дисперсий и средних квадратических отклонений [1-3].

Если  случайная величина X - дискретная,  то определяются ,  и оценки  значений функции вероятности  или оценки  значений функции распределения .

Если случайная величина X - непрерывная, то определяются М_х , D_х и оценки f_x(x), F_x(x) плотности вероятности f_x(x) и функции распределения F_x(x).

При оценивании законов распределения непрерывной случайной величины процесс обработки экспериментальных данных - реализаций х ,...,x_N,, начинается с выбора границ а и b > а интервала, заключающего возможные значения X, и деления этого интервала на k равных элементарных промежутков с = (b - a)/ k.

При расчете с значения а и b следует для удобства округлять,

принимая, например, вместо b = 3,341, а = -2,63 значения 3,4 и -2,7. Во всех случаях округление производится в сторону увеличения разности b- а. Значение k выбирается в пределах от 8 до 20. Удобно принять k= 10.

После этого определяют границы  всех элементарных промежутков и составляют таблицу (табл.1), в которой х'₀=а, x'_k=b. Значение  - это число реализаций X, оказавшихся в пределах j-ого интерва­ла от , до . Значения и :

 (32)
. (33)

При группировке реализаций X по отдельным интервалам может оказаться что некоторые из них придутся точно на границу двух смежных промежутков. В этих случаях необходимо прибавить к чис­лам и  смежных интервалов по 1/2.

 …   …     …     …  

По данным таблицы могут быть построены эмпирические гистограмма и график функции распределения.

Затем возникает весьма сложная задача подбора аналитического закона распределения, достаточно хорошо согласующегося с результатами эксперимента.

Основанием для выбора аналитического выражения плотности вероятности f_x(x) могут служить соображения о том, чтобы простейшие числовые характеристики теоретической случайной величины были равны экспериментальным значениям этих характеристик. Если, например, теоретический закон определяется двумя параметрами, то их выбирают так, чтобы совпали два момента ().

Похожие работы

Формирование комплексных программ природопользования

Скачать

35134

0

0

... их выполнения, к исполнителям и источникам ресурсов в достаточно дробной номенклатуре. 5. В качестве отдельного этапа разработки региональной программы природопользования следует выделить формирование организационной структуры управления программой. Его можно осуществить на базе классификационных алгоритмов, основанных на разбиении всего множества задач программы на относительно независимые ...

Некоторые системные и методологические аспекты информатики и информатизации

Скачать

30195

0

0

... причинно-следственных связей в системе, определения, описания, изучения систем. Важное методологическое значение при решении проблем информатизации имеют некоторые сформулированные в синергетике (школой Пригожина и др.) ключевые законы, среди которых (и применительно к социально-экономическим проблемам информатики) укажем основные: Для любой открытой системы информатизации характерна эволюция, ...

Экология землепользования как наука

Скачать

43758

0

0

... использования и охраны земельных ресурсов. Оно базируется на признанных классических положениях науки о землеустройстве, его определении как социально-экономическом и эколого-хозяйственном процессе и комплексе мероприятий по формированию объективно обусловленных систем землевладения (землепользования) и земельных отношений, территориальной организации сельскохозяйственного, промышленного и иного ...

Концепции современного естествознания

Скачать

451842

0

2

... о биологической причинности. Ряд феноменов, которые витализм считал специфическими для биологических объектов (способность к саморегуляции, усложнение строения, достижение одного результата разными способами) рассматриваются в современном естествознании как типичные проявления процессов самоорганизации любых достаточно сложных систем, а не только живых. Н.Бор: “ни один результат биологического ...