Навигация
Критерий интервальных оценок
32541
знак
0
таблиц
1
изображение
3.6 Критерий интервальных оценок
Располагая результатами эксперимента согласно (31) рассчитывают средние квадратические отклонения:
; 
.
(34)
Согласно (8) рассчитываются доверительные интервалы
и границы изменения ВВХ
,
(35)
соответствующие доверительной вероятности 
и 
.
Располагая выбранным аналитическим выражением плотности вероятности fx(x), рассчитываются теоретические значения:
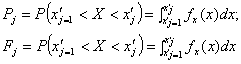(36)
Критерием согласия теоретического и экспериментального распределения является соблюдение неравенств:
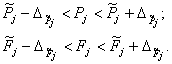(37)
Критерий 
Рассчитав 
согласно (35), находят значения
(38)
и рассчитывают
. (39)
Если расхождение между экспериментальным и теоретическим распределением несущественно, то распределение случайной величины (39) близко к нормальному с математическим ожиданием 
и
средним квадратическим отклонением 
, где s - так называемое число степеней свободы и согласно (8) с доверительной вероятностью рд = 0,997 справедливо неравенство
.
(40)
Число степеней свободы s = k - и - это разность между числом интервалов k, выбираемых произвольно, и числом условий и, которым должно удовлетворять эмпирическое распределение случайной величины. Этих условий обычно три: сумма всех 
равна единице, математическое ожидание равно 
дисперсия равна 
3.7 Сравнение математических ожиданий и дисперсий
Особой задачей, возникающей при экспериментальном исследовании случайных величин, является сравнение экспериментальных математических ожиданий 
и дисперсий 
, полученных в результате N1, и N2 независимых измерений случайных величин X1 и X2.
Для проверки гипотезы 
или, что то же самое 
, рассчитывается критерий [1-3]
.
(41)
Если 
, гипотезу можно признать справедливой с доверительной вероятностью 
= 0,9972 .
3.8 Использование модели случайных стационарных процессов для анализа динамики численности птиц
Для анализа ряда многолетних наблюдений динамики численности птиц были применены методы стационарных случайных процессов.
Численность (плотность) птиц рассчитывалась на объединенную площадь лесов и на объединенную площадь всех исследованных местообитаний.
С помощью метода автокорреляции были получены коррелограммы процессов изменения численности птиц за 12-летний период на объединенных площадях и площадях всех лесов. Подсчитаны коэффициенты автокорреляции и частной автокорреляции (наибольший коэффициент автокорреляции R1=0,63; частной автокорреляции Rpar 1=0,63). При исследовании коррелограмм не обнаружились характеристические свойства моделей скользящей средней и авторегрессионной модели, т.е. конечная протяженность автокорреляционной функции и частной автокорреляционной функции. Поэтому была выбрана смешанная модель авторегрессии-скользящей средней (АРСС).
Экологический смысл авторегрессионных параметров заключается в отражении периодичности изменения численности птиц в сезонном и многолетнем рассмотрении. Использование скользящей средней можно обосновать, ссылаясь на известное высказывание о том, что одним из простейших методов, позволяющих элиминировать случайные колебания эмпирической линии регрессии, является метод выравнивания способом скользящей средней (Биоиндикация…, 1994).
Подобранная модель имеет вид:
xt = xt-1+at - θat-1,
где x – прогнозирующая переменная авторегрессии,
а – скользящей средней,
θ – параметры смешанной модели.
Проверка адекватности модели, точнее, ее прогнозных качеств, производилась на усеченных рядах данных (10-летних). Прогноз рассчитывался на два года вперед и сравнивался с эмпирическими данными. Подсчет коэффициентов корреляции между опытными данными и прогнозом показал сильную связь для лесных местообитаний (непараметрический коэффициент корреляции Спирмена R=0,81) и меньшую связь для объединенных площадей (R=0,53). Ряды остатков подобранных моделей не обнаруживают какой-либо остаточной структуры, судя по полученным коррелограммам остатков. Заниженные прогнозные значения модели процесса не противоречат полученному нами ранее тренду небольшого многолетнего уменьшения численности птиц.
Построенная модель может служить для анализа и прогноза численности птиц.
Литература
1. Потемкин В.Г. МАТЛАБ. Справочное пособие, Изд-во «Диалог МИФИ», 1998 г.
2. Барабашева Ю.М., Девяткова Г.Н., Тутубалин В.Н., Угер Е.Г. Некоторые модели динамики численностей взаимодействующих видов с точки зрения математической статистики // Журнал общей биологии. – 1996. 57, N.2. – С.123 – 139.
3. Боголюбов А.Г. Математические модели эколого-генетических процессов конкуренции видов. Автореферат диссертации на соискание ученой степени доктора физико-математических наук. С.-Пб. 1995. – 34 с.
4. Болсуновский А.Я. Эколого-биофизические механизмы доминирования микроводорослей в культуре и водоеме. Автореферат диссертации на соискание ученой степени доктора биологических наук. Красноярск. 1999. – 48 с.
5. Гаузе Г.Ф. Исследования над борьбой за существование в смешанных популяциях // Зоол. журн. – 1935. 14, N.4. – С.243 – 270.
6. Замолодчиков Д.Г., Левич А.П., Рыбакова С.Ю. Исследование адекватности теоретико-категорной модели фитопланктонных сообществ // Проблемы экологического мониторинга и моделирования экосистем. Т.15. Л.: Гидрометеоиздат. 1993. – С.234 – 246.
7. Зотин А.И., Зотин А.А. Направление, скорость и механизмы прогрессивной эволюции: Термодинамические и экспериментальные основы. М.: Наука. 1999. – 320 с.
8. Крупаткина Д.К. Особенности роста фитопланктона в связи с содержанием биогенных элементов в клетках // Биология моря. – 1978. Вып.47. – С.18 – 25.
9. Кучай Л.А. Использование концепции клеточной квоты в моделях динамики фитопланктона. ДЕП 8567-В85. ВИНИТИ. 1985. – 35 с.
10. Левич А.П. Структура экологических сообществ. М.: Изд-во Моск. ун-та. 1980. – 181 с.
11. Левич А.П., Булгаков Н.Г., Замолодчиков Д.Г. Оптимизация структуры кормовых фитопланктонных сообществ. Под редакцией проф. В.Н.Максимова. М.: Товарищество научных издателей КМК. 1996б. – 136 с.
12. Минкевич И.Г., Андреев С.В., Ерошин В.К. Влияние органического и минерального субстратов на величину затрат клеток на поддержание // Микробиология. – 1998. 67, N.2. – С.176 – 181.
13. Печуркин Н.С. Энергетические аспекты развития надорганизменных систем. Новосибирск: Наука. 1982. – 112 c.
14. Приц А.К. Принцип стационарных состояний открытых систем и динамика популяций. Калининград. 1974. – 123 c.
15. Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных процессов. Учебное пособие. М.: Изд-во Моск. ун-та. 1993. – 302 c.
16. Розен Р. Принцип оптимальности в биологии. М.: Мир. 1969. – 215 c.
17. Свирежев Ю.М. Феноменологическая термодинамика взаимодействующих популяций // Журнал общей биологии. – 1991. 52, N.6. – С.840 – 853.
18. Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука. 1978. – 352 с.
19. Силкин В.А., Хайлов К.М. Биоэкологические механизмы управления в аквакультуре. Л.: Наука. 1988. – 230 c.
20. Страшкраба М., Гнаук А. Пресноводные экосистемы. Математическое моделирование. М.: Мир. 1989. – 376 c.
Похожие работы
... их выполнения, к исполнителям и источникам ресурсов в достаточно дробной номенклатуре. 5. В качестве отдельного этапа разработки региональной программы природопользования следует выделить формирование организационной структуры управления программой. Его можно осуществить на базе классификационных алгоритмов, основанных на разбиении всего множества задач программы на относительно независимые ...
... причинно-следственных связей в системе, определения, описания, изучения систем. Важное методологическое значение при решении проблем информатизации имеют некоторые сформулированные в синергетике (школой Пригожина и др.) ключевые законы, среди которых (и применительно к социально-экономическим проблемам информатики) укажем основные: Для любой открытой системы информатизации характерна эволюция, ...
... использования и охраны земельных ресурсов. Оно базируется на признанных классических положениях науки о землеустройстве, его определении как социально-экономическом и эколого-хозяйственном процессе и комплексе мероприятий по формированию объективно обусловленных систем землевладения (землепользования) и земельных отношений, территориальной организации сельскохозяйственного, промышленного и иного ...
... о биологической причинности. Ряд феноменов, которые витализм считал специфическими для биологических объектов (способность к саморегуляции, усложнение строения, достижение одного результата разными способами) рассматриваются в современном естествознании как типичные проявления процессов самоорганизации любых достаточно сложных систем, а не только живых. Н.Бор: “ни один результат биологического ...
0 комментариев