Аналитическое выравнивание

2. Аналитическое выравнивание

Выберем в качестве функций регрессии – линейную, параболическую, гиперболическую и показательную:

 .

Гиперболическую и показательную можно линеаризовать и применить МНК к этим функциям как к линейным. Для гиперболической функции введем новую переменную:

.

Тогда получим:

,

где

.

Для показательной функции проведем следующие преобразования. Прологарифмируем обе части уравнения: . Сделаем замены:

, , .

Получим:

,

откуда найдем: , , .

Применим ПО MS Excel 2003 и Stata 7.0. Посчитаем коэффициент корреляции:

Коэффициент корреляции значим.

Построим линейную регрессию

Регрессионная статистика
Множественный R	0,717687
R-квадрат	0,515074
Нормированный R-квадрат	0,491982
Стандартная ошибка	3,693991
Наблюдения	23
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	304,3725	304,3725	22,30559	0,000116
Остаток	21	286,557	13,64557
Итого	22	590,9296
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	3,014625	1,592152	1,893427	0,072162	-0,29644	6,325686
Переменная X 1	0,548419	0,11612	4,722879	0,000116	0,306935	0,789903

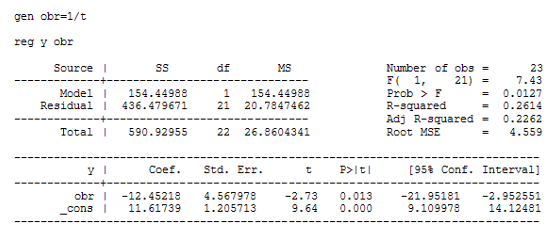
Регрессия для гиперболической функции:

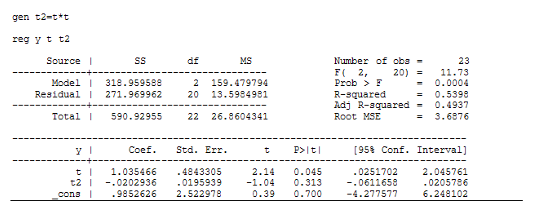
Регрессия для параболической функции:

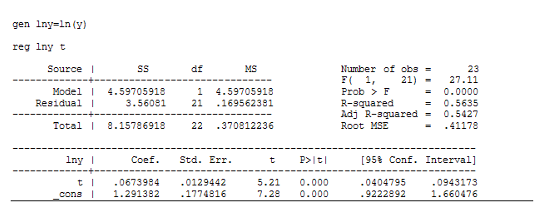
Регрессия для показательной функции:

Как видно из этих данных, коэффициент детерминации у регрессии для гиперболической функции значительно хуже, чем у других моделей. А константа и коэффициент при переменной  в модели параболической регрессии не значимы согласно t-критерию Стьюдента.

Коэффициенты детерминации для моделей линейной и показательной регрессий примерно одиноковы, причем R-квадрат больше у показательной регрессии. Сравним эти 2 модели по другим показателям. Рассчитаем среднюю квадратическую ошибку уравнения тренда и информационные критерии Акейка и Шварца:

, ,

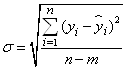Чем меньше значение информационных критериев, тем лучше модель.

Итак, для модели линейной регрессии получим:

AIC=5,131843277

BIC=2,658769213 σ=3,694

Для модели регрессии показательной функции имеем:

AIC= 5,477785725 BIC= 2,831740437 σ=4,028

Все 3 показателя лучше в первом случае.

Применим модель линейной регрессии для аналитического выравнивания исходного ряда. Модель такова:

у=3,01+0,55t;

Значения уровней ряда, полученных по модели, и остатков представлены в следующей таблице:

Наблюдение	Предсказанное Y	Остатки
1	3,563043478	-0,063043478
2	4,111462451	1,088537549
3	4,659881423	-2,459881423
4	5,208300395	-1,608300395
5	5,756719368	1,343280632
6	6,30513834	0,59486166
7	6,853557312	-2,753557312
8	7,401976285	-2,101976285
9	7,950395257	2,149604743
10	8,498814229	-3,698814229
11	9,047233202	-1,347233202
12	9,595652174	7,204347826
13	10,14407115	-0,344071146
14	10,69249012	3,807509881
15	11,24090909	2,459090909
16	11,78932806	7,210671937
17	12,33774704	-7,337747036
18	12,88616601	-0,886166008
19	13,43458498	-2,13458498
20	13,98300395	3,516996047
21	14,53142292	-1,431422925
22	15,0798419	2,820158103
23	15,62826087	-6,02826087

Спрогнозируем урожайность озимой пшеницы на последующие 6 лет

Прогнозные значения
t	y
24	16,17667984
25	16,72509881
26	17,27351779
27	17,82193676
28	18,37035573
29	18,9187747

Из графика видно, что урожайность с каждым последующим годом будет возрастать и достигнет через шесть лет значения практически в 2 раза большего, чем в 1969 году. Этот результат достигнут в результате существенного роста урожайности зерновых культур.

Проверим наличие автокорреляции в данном динамическом ряду. Для этого составим следующие таблицы:

Расчет коэффициента автокорреляции 1-го порядка

Год	Фактические уровни y(t)	Уровни, сдвинутые на год y(t-1)	y(t)y(t-1)	y(t)^2
1	3,5	9,6	33,6	12,25
2	5,2	3,5	18,2	27,04
3	2,2	5,2	11,44	4,84
4	3,6	2,2	7,92	12,96
5	7,1	3,6	25,56	50,41
6	6,9	7,1	48,99	47,61
7	4,1	6,9	28,29	16,81
8	5,3	4,1	21,73	28,09
9	10,1	5,3	53,53	102,01
10	4,8	10,1	48,48	23,04
11	7,7	4,8	36,96	59,29
12	16,8	7,7	129,36	282,24
13	9,8	16,8	164,64	96,04
14	14,5	9,8	142,1	210,25
15	13,7	14,5	198,65	187,69
16	19	13,7	260,3	361
17	5	19	95	25
18	12	5	60	144
19	11,3	12	135,6	127,69
20	17,5	11,3	197,75	306,25
21	13,1	17,5	229,25	171,61
22	17,9	13,1	234,49	320,41
23	9,6	17,9	171,84	92,16
Сумма	220,7	220,7	2353,68	2708,69
Средняя	9,595652174		102,333913	117,76913
	Дисперсия	25,69258979	Автокорреляция присутствует ( с вероятностью 0,95)
Коэффициент автокорреляции		0,399234662

Расчет коэффициента автокорреляции 2-го порядка

Год	Фактические уровни y(t)	Уровни, сдвинутые на 2 года y(t-2)	y(t)y(t-2)	y(t)^2
1	3,5	17,9	62,65	12,25
2	5,2	9,6	49,92	27,04
3	2,2	3,5	7,7	4,84
4	3,6	5,2	18,72	12,96
5	7,1	2,2	15,62	50,41
6	6,9	3,6	24,84	47,61
7	4,1	7,1	29,11	16,81
8	5,3	6,9	36,57	28,09
9	10,1	4,1	41,41	102,01
10	4,8	5,3	25,44	23,04
11	7,7	10,1	77,77	59,29
12	16,8	4,8	80,64	282,24
13	9,8	7,7	75,46	96,04
14	14,5	16,8	243,6	210,25
15	13,7	9,8	134,26	187,69
16	19	14,5	275,5	361
17	5	13,7	68,5	25
18	12	19	228	144
19	11,3	5	56,5	127,69
20	17,5	12	210	306,25
21	13,1	11,3	148,03	171,61
22	17,9	17,5	313,25	320,41
23	9,6	13,1	125,76	92,16
Сумма	220,7	220,7	2349,25	2708,69
Средняя	9,595652174		102,141304	117,76913
	Дисперсия	25,69258979	Автокорреляция присутствует ( с вероятностью 0,99)
Коэффициент автокорреляции		0,391737999

Расчет коэффициента автокорреляции 3-го порядка

Год	Фактические уровни y(t)	Уровни, сдвинутые на 3 года y(t-3)	y(t)y(t-3)	y(t)^2
1	3,5	13,1	45,85	12,25
2	5,2	17,9	93,08	27,04
3	2,2	9,6	21,12	4,84
4	3,6	3,5	12,6	12,96
5	7,1	5,2	36,92	50,41
6	6,9	2,2	15,18	47,61
7	4,1	3,6	14,76	16,81
8	5,3	7,1	37,63	28,09
9	10,1	6,9	69,69	102,01
10	4,8	4,1	19,68	23,04
11	7,7	5,3	40,81	59,29
12	16,8	10,1	169,68	282,24
13	9,8	4,8	47,04	96,04
14	14,5	7,7	111,65	210,25
15	13,7	16,8	230,16	187,69
16	19	9,8	186,2	361
17	5	14,5	72,5	25
18	12	13,7	164,4	144
19	11,3	19	214,7	127,69
20	17,5	5	87,5	306,25
21	13,1	12	157,2	171,61
22	17,9	11,3	202,27	320,41
23	9,6	17,5	168	92,16
Сумма	220,7	220,7	2218,62	2708,69
Средняя	9,595652174		96,4617391	117,76913
	Дисперсия	25,69258979	Автокорреляция отсутствует
Коэффициент автокорреляции		0,170679504

Как видно из таблиц, обнаружилась автокорреляция только первого и второго порядков. Это говорит о том, что значительное влияние на урожайность озимой пшеницы в данном году оказывает урожайность двух предыдущих лет.