Навигация
Метод скользящих средних
4. Метод скользящих средних
Выберем в качестве параметров скольжения 3, 5, 9. Причем при параметре, равном 5, используем весовые коэффициенты для расчета скользящей средней. Для определения этих весовых коэффициентов применим треугольник Паскаля. Таким образом, весовыми коэффициенты будут следующие числа: 1, 2, 4, 2, 1.
Для начала проведем расчеты при параметре скольжения 3. Данные приведем в следующей таблице:
| t | y | Скользящая сумма | Скользящая средняя | Прирост | Ускорения |
| 1 | 3,5 | ||||
| 2 | 5,2 | 25,1 | 8,367 | ||
| 3 | 2,2 | 22,1 | 7,367 | -1 | |
| 4 | 3,6 | 25,1 | 8,367 | 1 | 2 |
| 5 | 7,1 | 29 | 9,667 | 1,3 | 0,3 |
| 6 | 6,9 | 31,8 | 10,6 | 0,933 | -0,367 |
| 7 | 4,1 | 29 | 9,667 | -0,933 | -1,867 |
| 8 | 5,3 | 33,7 | 11,233 | 1,567 | 2,500 |
| 9 | 10,1 | 32,7 | 10,9 | -0,333 | -1,900 |
| 10 | 4,8 | 39,6 | 13,2 | 2,300 | 2,633 |
| 11 | 7,7 | 40,1 | 13,367 | 0,167 | -2,133 |
| 12 | 16,8 | 49,4 | 16,467 | 3,100 | 2,933 |
| 13 | 9,8 | 51,5 | 17,167 | 0,700 | -2,400 |
| 14 | 14,5 | 56,2 | 18,733 | 1,567 | 0,867 |
| 15 | 13,7 | 59,4 | 19,8 | 1,067 | -0,500 |
| 16 | 19 | 49,6 | 16,533 | -3,267 | -4,333 |
| 17 | 5 | 48,7 | 16,233 | -0,300 | 2,967 |
| 18 | 12 | 45,3 | 15,1 | -1,133 | -0,833 |
| 19 | 11,3 | 57,4 | 19,133 | 4,033 | 5,167 |
| 20 | 17,5 | 49,7 | 16,567 | -2,567 | -6,600 |
| 21 | 13,1 | 51,5 | 17,167 | 0,600 | 3,167 |
| 22 | 17,9 | 45,3 | 15,1 | -2,067 | -2,667 |
| 23 | 9,6 |
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
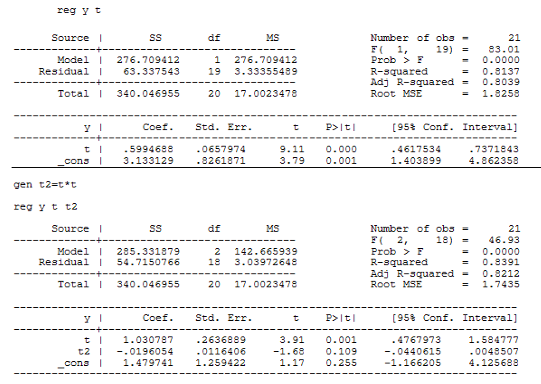
Выберем модель параболической регрессии на основании лучших коэффициента детерминации и скорректированного коэффициента детерминации у этой модели. Получим следующую модель:
y=1.4+1.03t-0.02 ![]()
Спрогнозируем значения скользящих средних на последующие 6 лет:
| t |
|
| 23 | 16,4389 |
| 24 | 16,0816 |
| 25 | 15,6469 |
| 26 | 15,1348 |
| 27 | 14,5454 |
| 28 | 13,8786 |
Рассчитаем значения исходного ряда на будущий период, используя формулу:
![]()
и приведем в следующей таблице:
| Значения скользящих средних, полученные по модели | t | Значения у |
| 1 | 3,5 | |
| 8,51976912 | 2 | 5,2 |
| 9,052236652 | 3 | 2,2 |
| 9,584704185 | 4 | 3,6 |
| 10,11717172 | 5 | 7,1 |
| 10,64963925 | 6 | 6,9 |
| 11,18210678 | 7 | 4,1 |
| 11,71457431 | 8 | 5,3 |
| 12,24704185 | 9 | 10,1 |
| 12,77950938 | 10 | 4,8 |
| 13,31197691 | 11 | 7,7 |
| 13,84444444 | 12 | 16,8 |
| 14,37691198 | 13 | 9,8 |
| 14,90937951 | 14 | 14,5 |
| 15,44184704 | 15 | 13,7 |
| 15,97431457 | 16 | 19 |
| 16,50678211 | 17 | 5 |
| 17,03924964 | 18 | 12 |
| 17,57171717 | 19 | 11,3 |
| 18,1041847 | 20 | 17,5 |
| 18,63665224 | 21 | 13,1 |
| 19,16911977 | 22 | 17,9 |
| 16,3222 | 23 | 9,6 |
| Прогноз на будущее | ||
| 16,9218 | 24 | 21,47 |
| 17,5214 | 25 | 19,70 |
| 18,1209 | 26 | 11,40 |
| 18,7205 | 27 | 23,27 |
| 19,3201 | 28 | 21,50 |
| 29 | 13,20 | |
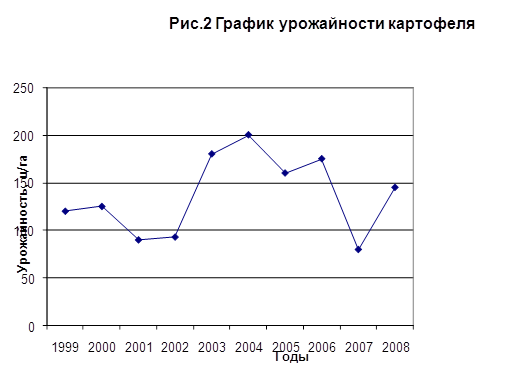
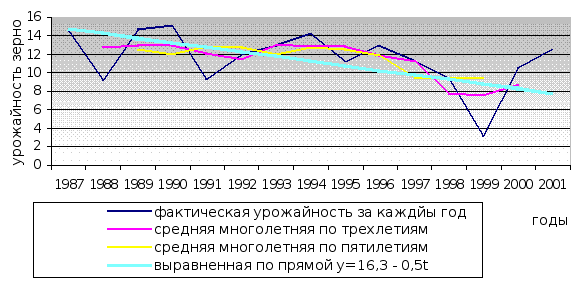
Значения урожайности по годам вместе с прогнозными значениями представим на графике:
Проведем расчеты для параметра 5 с применением треугольника Паскаля.
| t | y | Скользящая сумма | Скользящая средняя | Прирост | Ускорения |
| 1 | 3,5 | ||||
| 2 | 5,2 | ||||
| 3 | 2,2 | 37 | 3,700 | ||
| 4 | 3,6 | 45,1 | 4,510 | 0,81 | |
| 5 | 7,1 | 55,7 | 5,570 | 1,06 | 0,25 |
| 6 | 6,9 | 58,9 | 5,890 | 0,320 | -0,740 |
| 7 | 4,1 | 58 | 5,800 | -0,090 | -0,410 |
| 8 | 5,3 | 61,3 | 6,130 | 0,330 | 0,420 |
| 9 | 10,1 | 72,4 | 7,240 | 1,110 | 0,780 |
| 10 | 4,8 | 76,9 | 7,690 | 0,450 | -0,660 |
| 11 | 7,7 | 93,9 | 9,390 | 1,700 | 1,250 |
| 12 | 16,8 | 121,5 | 12,150 | 2,760 | 1,060 |
| 13 | 9,8 | 123,2 | 12,320 | 0,170 | -2,590 |
| 14 | 14,5 | 140,8 | 14,080 | 1,760 | 1,590 |
| 15 | 13,7 | 136,6 | 13,660 | -0,420 | -2,180 |
| 16 | 19 | 139,9 | 13,990 | 0,330 | 0,750 |
| 17 | 5 | 107 | 10,700 | -3,290 | -3,620 |
| 18 | 12 | 117,1 | 11,710 | 1,010 | 4,300 |
| 19 | 11,3 | 122,3 | 12,230 | 0,520 | -0,490 |
| 20 | 17,5 | 148,7 | 14,870 | 2,640 | 2,120 |
| 21 | 13,1 | 144,1 | 14,410 | -0,460 | -3,100 |
| 22 | 17,9 | ||||
| 23 | 9,6 |
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
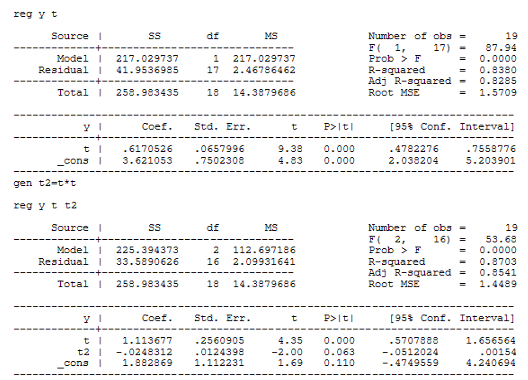
Выберем модель параболической регрессии на основании лучших R-квадрата и скорректированного R-квадрата у этой модели. Получим следующую модель:
y=1.88+1.11t-0.02![]()
Отобразим ее на графике:
Спрогнозируем значения скользящих средних на последующие 6 лет:
| t |
|
| 23 | 17,1962 |
| 24 | 17,8133 |
| 25 | 18,4303 |
| 26 | 19,0474 |
| 27 | 19,6644 |
| 28 | 20,2815 |
Рассчитаем значения исходного ряда на будущий период, используя формулу:
![]()
и приведем в следующей таблице:
| Значения скользящих средних, полученные по модели | t | Значения у |
| 1 | 3,5 | |
| 2 | 5,2 | |
| 8,8125 | 3 | 2,2 |
| 9,3924 | 4 | 3,6 |
| 9,9723 | 5 | 7,1 |
| 10,5522 | 6 | 6,9 |
| 11,1321 | 7 | 4,1 |
| 11,7120 | 8 | 5,3 |
| 12,2919 | 9 | 10,1 |
| 12,8718 | 10 | 4,8 |
| 13,4517 | 11 | 7,7 |
| 14,0316 | 12 | 16,8 |
| 14,6115 | 13 | 9,8 |
| 15,1914 | 14 | 14,5 |
| 15,7713 | 15 | 13,7 |
| 16,3512 | 16 | 19 |
| 16,9311 | 17 | 5 |
| 17,5109 | 18 | 12 |
| 18,0908 | 19 | 11,3 |
| 18,6707 | 20 | 17,5 |
| 19,2506 | 21 | 13,1 |
| 15,9621 | 22 | 17,9 |
| 16,5792 | 23 | 9,6 |
| Прогноз на будущее | ||
| 17,1962 | 24 | 25,12 |
| 17,8133 | 25 | 28,25 |
| 18,4303 | 26 | -22,12 |
| 19,0474 | 27 | 49,53 |
| 28 | 92,10 | |
| 29 | -175,87 | |
Из таблицы видно, что при t=29 значение урожайности отрицательное, чего не может быть в принципе. Этот факт объясняется тем, что исходный ряд плохо аппроксимируется нормальным распределением.
Проведем расчеты при параметре скольжения 9. Данные приведем в следующей таблице:
| t | y | Скользящая сумма | Скользящая средняя | Прирост | Ускорения |
| 1 | 3,5 | ||||
| 2 | 5,2 | ||||
| 3 | 2,2 | ||||
| 4 | 3,6 | ||||
| 5 | 7,1 | 48 | 5,333 | ||
| 6 | 6,9 | 49,3 | 5,478 | 0,144 | |
| 7 | 4,1 | 51,8 | 5,756 | 0,278 | 0,133 |
| 8 | 5,3 | 66,4 | 7,378 | 1,622 | 1,344 |
| 9 | 10,1 | 72,6 | 8,067 | 0,689 | -0,933 |
| 10 | 4,8 | 80 | 8,889 | 0,822 | 0,133 |
| 11 | 7,7 | 86,8 | 9,644 | 0,756 | -0,067 |
| 12 | 16,8 | 101,7 | 11,300 | 1,656 | 0,900 |
| 13 | 9,8 | 101,4 | 11,267 | -0,033 | -1,689 |
| 14 | 14,5 | 103,3 | 11,478 | 0,211 | 0,244 |
| 15 | 13,7 | 109,8 | 12,200 | 0,722 | 0,511 |
| 16 | 19 | 119,6 | 13,289 | 1,089 | 0,367 |
| 17 | 5 | 115,9 | 12,878 | -0,411 | -1,500 |
| 18 | 12 | 124 | 13,778 | 0,900 | 1,311 |
| 19 | 11,3 | 119,1 | 13,233 | -0,544 | -1,444 |
| 20 | 17,5 | ||||
| 21 | 13,1 | ||||
| 22 | 17,9 | ||||
| 23 | 9,6 |
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
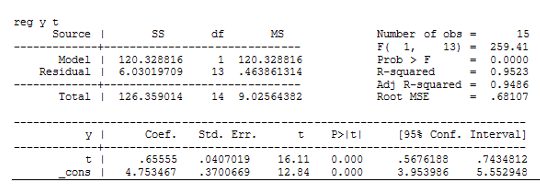
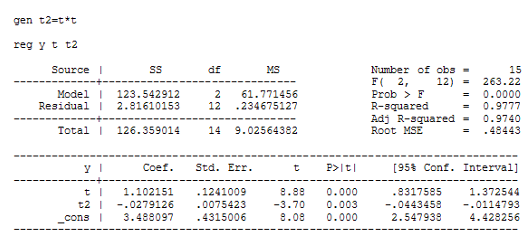
Выберем модель параболической регрессии на основании лучших R-квадрата и скорректированного R-квадрата у этой модели. Получим следующую модель:
y=3.49+1.1t-3.49![]()
Спрогнозируем значения скользящих средних на последующие 6 лет:
| t |
|
| 23 | 17,8644 |
| 24 | 18,5200 |
| 25 | 19,1756 |
| 26 | 19,8311 |
| 27 | 20,4867 |
| 28 | 21,1422 |
Рассчитаем значения исходного ряда на будущий период, используя формулу:
![]()
и приведем в следующей таблице:
| Значения скользящих средних, полученные по модели | t | Значения у |
| 1 | 3,5 | |
| 2 | 5,2 | |
| 3 | 2,2 | |
| 4 | 3,6 | |
| 9,9721 | 5 | 7,1 |
| 10,5981 | 6 | 6,9 |
| 11,2241 | 7 | 4,1 |
| 11,8501 | 8 | 5,3 |
| 12,4761 | 9 | 10,1 |
| 13,1021 | 10 | 4,8 |
| 13,7281 | 11 | 7,7 |
| 14,3541 | 12 | 16,8 |
| 14,9801 | 13 | 9,8 |
| 15,6061 | 14 | 14,5 |
| 16,2321 | 15 | 13,7 |
| 16,8580 | 16 | 19 |
| 17,4840 | 17 | 5 |
| 18,1100 | 18 | 12 |
| 18,7360 | 19 | 11,3 |
| 15,2422 | 20 | 17,5 |
| 15,8978 | 21 | 13,1 |
| 16,5533 | 22 | 17,9 |
| 17,2089 | 23 | 9,6 |
| Прогноз на будущее | ||
| 16,6847 | 24 | 51,99 |
| 16,2773 | 25 | 18,31 |
| 26 | 3,56 | |
| 27 | 9,82 | |
| 28 | 8,38 | |
| 29 | 13,83 | |
Похожие работы
... . А различное соотношение и распределение почв наложили, в свою очередь, отпечаток на производительность почвенного покрова хозяйств и районов области. 4. Авторегрессионое прогнозирование урожайности зерновых культур Для характеристики направления и интенсивности развития изучаемого явления рассчитаем систему показателей динамики посевной площади зерновых культур в Покровском районе ...
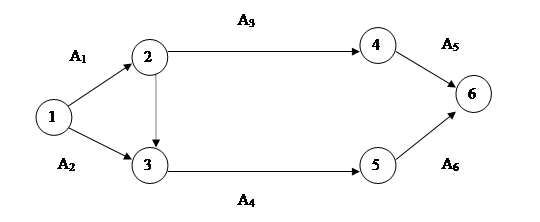
... в построении модели, можно исправить в последующих циклах. В методологии моделирования, таким образом, заложены большие возможности саморазвития. Таким образом, мы рассмотрели сущность моделирования. Метод экономического моделирования, это одна из подгрупп метода прогнозирования. Особенность его применения в прогнозировании заключается в следующем: основа метода – сетевой график, имеющий много ...
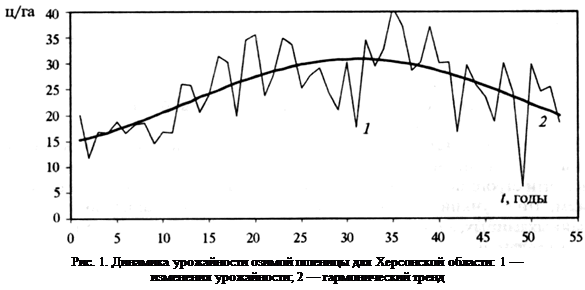
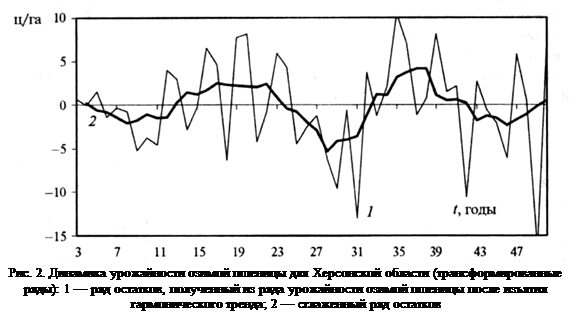
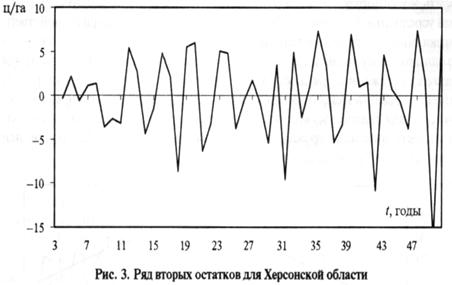
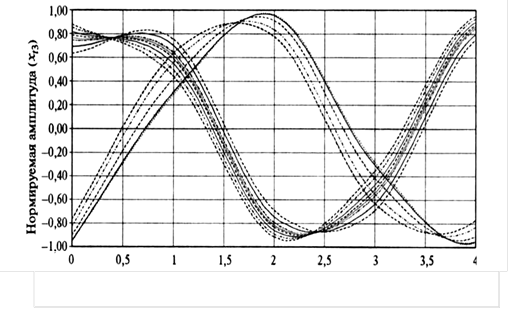
... гг.) позволило выделить средний цикл продолжительностью 18-19 лет и короткий цикл продолжительностью 2,5 года. Следовательно, можно утверждать, что цикл средней продолжительности (от 14 до 19 лет) характерен для динамики урожайности зерновых, независимо от природно-климатических условий территории. Короткий цикл урожайности проявляется достаточно четко в Степной зоне Украины, но менее заметен для ...
... является фондоотдача. Но происходит это из-за отсутствия новой техники, не возобновления основных фондов и прочих негативных факторов, возникающих в сельскохозяйственном производстве. 3. Экономико-статистический анализ урожая и урожайности зерновых. Статистика урожайности ставит своей целью объяснить причины различий и происшедших изменений в уровнях урожайности в различных районах, хозяйствах и ...
0 комментариев