Навигация
Выравнивание при помощи рядов Фурье
5. Выравнивание при помощи рядов Фурье
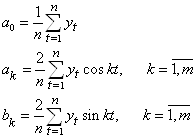
Пусть ряд содержит циклическую составляющую, выраженную некоторой функцией от времени y(t) c известными периодами, нацело делящими n. То есть периоды y(t) задаются числами n/kj, j=1, …, m, где (k1, …,km) – подмножество последовательности целых чисел 1, …, (n-1)/2, если n нечетное. Представим y(t) в виде ряда Фурье – линейной комбинации синусов и косинусов для n нечетного:
![]()
Рассмотрим теперь задачу гармонического анализа ряда, состоящую в оценивании параметров a0, ak, bk:
Последовательные значения t определяются 0 с увеличением, равным ![]() .
.
Расчет показателей, необходимых для выравнивания с помощью ряда Фурье, представлен в следующей таблице:
| Год | t | y | y cos t | y sin t |
| y cos 2t | y sin 2t |
| ||
| 1 | 0 | 3,5 | 3,5 | 0 | 7,765 | 18,192 | 3,5 | 0 | 8,132 | 21,456 |
| 2 | 0,273 | 5,2 | 5,007 | 1,403 | 6,611 | 1,992 | 4,443 | 2,702 | 6,252 | 1,107 |
| 3 | 0,546 | 2,2 | 1,880 | 1,143 | 5,679 | 12,103 | 1,012 | 1,953 | 4,698 | 6,242 |
| 4 | 0,820 | 3,6 | 2,457 | 2,631 | 5,037 | 2,065 | -0,246 | 3,592 | 3,721 | 0,015 |
| 5 | 1,093 | 7,1 | 3,266 | 6,304 | 4,733 | 5,602 | -4,094 | 5,800 | 3,464 | 13,220 |
| 6 | 1,366 | 6,9 | 1,403846 | 6,756 | 4,790 | 4,452 | -6,329 | 2,749 | 3,938 | 8,775 |
| 7 | 1,639 | 4,1 | -0,280 | 4,090 | 5,203 | 1,217 | -4,062 | -0,558 | 5,016 | 0,839 |
| 8 | 1,912 | 5,3 | -1,775 | 4,994 | 5,942 | 0,412 | -4,111 | -3,345 | 6,474 | 1,379 |
| 9 | 2,185 | 10,1 | -5,824 | 8,251 | 6,952 | 9,910 | -3,382 | -9,517 | 8,049 | 4,207 |
| 10 | 2,459 | 4,8 | -3,723 | 3,029 | 8,158 | 11,276 | 0,977 | -4,700 | 9,500 | 22,090 |
| 11 | 2,732 | 7,7 | -7,06253 | 3,068 | 9,471 | 3,135 | 5,256 | -5,627 | 10,667 | 8,803 |
| 12 | 3,005 | 16,8 | -16,644 | 2,288 | 10,792 | 36,090 | 16,177 | -4,533 | 11,495 | 28,143 |
| 13 | 3,278 | 9,8 | -9,709 | -1,334 | 12,026 | 4,953 | 9,437 | 2,644 | 12,030 | 4,971 |
| 14 | 3,551 | 14,5 | -13,300 | -5,777 | 13,0785 | 2,021 | 9,897 | 10,597 | 12,383 | 4,482 |
| 15 | 3,825 | 13,7 | -10,627 | -8,646 | 13,873 | 0,030 | 2,787 | 13,413 | 12,680 | 1,040 |
| 16 | 4,098 | 19 | -10,9569 | -15,522 | 14,350 | 21,618 | -6,363 | 17,903 | 13,008 | 35,905 |
| 17 | 4,371 | 5 | -1,674 | -4,711 | 14,475 | 89,779 | -3,879 | 3,155 | 13,374 | 70,119 |
| 18 | 4,644 | 12 | -0,819 | -11,972 | 14,238 | 5,009 | -11,888 | 1,634 | 13,698 | 2,884 |
| 19 | 4,917 | 11,3 | 2,299 | -11,064 | 13,657 | 5,553 | -10,364 | -4,502 | 13,836 | 6,430 |
| 20 | 5,190 | 17,5 | 8,051 | -15,538 | 12,774 | 22,336 | -10,092 | -14,297 | 13,620 | 15,056 |
| 21 | 5,464 | 13,1 | 8,941446 | -9,574 | 11,656 | 2,087 | -0,894 | -13,069 | 12,922 | 0,032 |
| 22 | 5,737 | 17,9 | 15,294 | -9,301 | 10,3844 | 56,485 | 8,235 | -15,893 | 11,702 | 38,410 |
| 23 | 6,010 | 9,6 | 9,244 | -2,590 | 9,055 | 0,297 | 8,202 | -4,988 | 10,041 | 0,194 |
| n=23 | ∑ | 220,7 | -21,050 | -52,072 | 220,7 | 316,615 | 4,219 | -14,886 | 220,700 | 295,799 |
| Год | t | y | y cos 3t | y sin 3t |
| (yi-yi2) |
| 1 | 0 | 3,5 | 3,5 | 0 | 6,496 | 8,976 |
| 2 | 0,273 | 5,2 | 3,549 | 3,800 | 3,47017 | 2,992 |
| 3 | 0,546 | 2,2 | -0,150 | 2,195 | 2,5366 | 0,113 |
| 4 | 0,820 | 3,6 | -2,793 | 2,272 | 3,55156 | 0,002 |
| 5 | 1,093 | 7,1 | -7,034 | -0,967 | 5,39523 | 2,906 |
| 6 | 1,366 | 6,9 | -3,979 | -5,637 | 6,74298 | 0,025 |
| 7 | 1,639 | 4,1 | 0,834 | -4,014 | 6,91425 | 7,920 |
| 8 | 1,912 | 5,3 | 4,528 | -2,754 | 6,26056 | 0,923 |
| 9 | 2,185 | 10,1 | 9,725 | 2,725 | 5,85861 | 17,989 |
| 10 | 2,459 | 4,8 | 2,208 | 4,262 | 6,72393 | 3,702 |
| 11 | 2,732 | 7,7 | -2,579 | 7,255 | 9,06763 | 1,870 |
| 12 | 3,005 | 16,8 | -15,409 | 6,693 | 12,0877 | 22,206 |
| 13 | 3,278 | 9,8 | -8,989 | -3,904 | 14,4381 | 21,512 |
| 14 | 3,551 | 14,5 | -4,856 | -13,663 | 15,0781 | 0,334 |
| 15 | 3,825 | 13,7 | 6,303 | -12,164 | 13,9511 | 0,063 |
| 16 | 4,098 | 19 | 18,295 | -5,126 | 12,0474 | 48,339 |
| 17 | 4,371 | 5 | 4,272 | 2,598 | 10,7918 | 33,545 |
| 18 | 4,644 | 12 | 2,441 | 11,749 | 11,1343 | 0,749 |
| 19 | 4,917 | 11,3 | -6,516 | 9,232 | 12,9175 | 2,616 |
| 20 | 5,190 | 17,5 | -17,337 | 2,383 | 14,9303 | 6,603 |
| 21 | 5,464 | 13,1 | -10,162 | -8,267 | 15,6291 | 6,396 |
| 22 | 5,737 | 17,9 | -1,222 | -17,858 | 14,0876 | 14,534 |
| 23 | 6,010 | 9,6 | 6,553 | -7,016 | 10,5895 | 0,979 |
| n=23 | ∑ | 220,7 | -18,815 | -26,207 | 220,7 | 205,297 |
Рассчитаем параметры:
| a0 | a1 | b1 | a2 | b2 | a3 | b3 |
| 9,596 | -1,830 | -4,528 | 0,367 | -1,294 | -1,636 | -2,279 |
Таким образом, получили модели:
- для гармоники первого порядка ![]() = 9,569-1,83 cos t-4.528 sin t
= 9,569-1,83 cos t-4.528 sin t
- для гармоники второго порядка ![]() = 9,569-1,83 cos t-4.528 sin t +
= 9,569-1,83 cos t-4.528 sin t +
+ 0,367 соs 2t-1.294 sin 2t
- для гармоники третьего порядка ![]() =9,569-1,83 cos t-4.528 sin t +
=9,569-1,83 cos t-4.528 sin t +
+ 0,367 соs 2t-1.294 sin 2t-1.636 cos3t-2.279 sin 3t
Исследуем модель с гармоникой первого порядка
Прогнозные значения
| Год | t |
|
| 24 | 6,283 | 7,765199 |
| 25 | 6,556 | 6,611 |
| 26 | 6,830 | 5,679 |
| 27 | 7,103 | 5,037 |
| 28 | 7,376 | 4,733 |
| 29 | 7,649 | 4,790 |
Изучим модель с гармоникой второго порядка
Прогнозные значения
| Год | t |
|
| 24 | 6,283 | 8,132054 |
| 25 | 6,556 | 6,252 |
| 26 | 6,830 | 4,698 |
| 27 | 7,103 | 3,721 |
| 28 | 7,376 | 3,464 |
| 29 | 7,649 | 3,938 |
Исследуем модель с гармоникой третьего порядка
Прогнозные значения
| Год | t |
|
| 24 | 6,283 | 6,496 |
| 25 | 6,556 | 3,470 |
| 26 | 6,830 | 2,537 |
| 27 | 7,103 | 3,552 |
| 28 | 7,376 | 5,395 |
| 29 | 7,649 | 6,743 |
Выводы
Были рассмотрены четыре метода прогнозирования – аналитическое выравнивание методом наименьших квадратов, метод экспоненциального сглаживания, метод скользящих средних, и выравнивание при помощи рядов Фурье. Выберем наиболее подходящий метод, который дает наиболее правдоподобный прогноз.
Выравнивание с помощью рядов Фурье дает сумму квадратов ошибок от 200 до 300 (в зависимости от гармоники). Метод экспоненциального сглаживания дает результат получше: для параболического тренда сумма квадратов ошибок колеблется от 36 до 115 (при ![]() сумма квадратов ошибок равна 115; при
сумма квадратов ошибок равна 115; при ![]() =0,4 сумма квадратов ошибок 36);Для линейной тенденции сумма квадратов ошибок равна 55. Аналитическое выравнивание МНК дает сумму квадратов ошибок, равную 272. Лучше всего описывает тренд метод скользящих средних с параметром n=3. Он дает сумму квадратов ошибок, равную 63.
=0,4 сумма квадратов ошибок 36);Для линейной тенденции сумма квадратов ошибок равна 55. Аналитическое выравнивание МНК дает сумму квадратов ошибок, равную 272. Лучше всего описывает тренд метод скользящих средних с параметром n=3. Он дает сумму квадратов ошибок, равную 63.
Похожие работы
... . А различное соотношение и распределение почв наложили, в свою очередь, отпечаток на производительность почвенного покрова хозяйств и районов области. 4. Авторегрессионое прогнозирование урожайности зерновых культур Для характеристики направления и интенсивности развития изучаемого явления рассчитаем систему показателей динамики посевной площади зерновых культур в Покровском районе ...
... в построении модели, можно исправить в последующих циклах. В методологии моделирования, таким образом, заложены большие возможности саморазвития. Таким образом, мы рассмотрели сущность моделирования. Метод экономического моделирования, это одна из подгрупп метода прогнозирования. Особенность его применения в прогнозировании заключается в следующем: основа метода – сетевой график, имеющий много ...
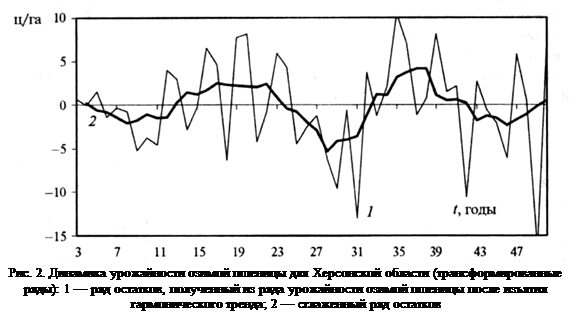
... гг.) позволило выделить средний цикл продолжительностью 18-19 лет и короткий цикл продолжительностью 2,5 года. Следовательно, можно утверждать, что цикл средней продолжительности (от 14 до 19 лет) характерен для динамики урожайности зерновых, независимо от природно-климатических условий территории. Короткий цикл урожайности проявляется достаточно четко в Степной зоне Украины, но менее заметен для ...
... является фондоотдача. Но происходит это из-за отсутствия новой техники, не возобновления основных фондов и прочих негативных факторов, возникающих в сельскохозяйственном производстве. 3. Экономико-статистический анализ урожая и урожайности зерновых. Статистика урожайности ставит своей целью объяснить причины различий и происшедших изменений в уровнях урожайности в различных районах, хозяйствах и ...
0 комментариев