Навигация
Определим число наблюдений: n = 9
1. Определим число наблюдений: n = 9
2. Найдем выборочное среднее для рядов: х = 1 / n Σ ni = 1 * x i
х1 = (1*(30,8 + 34,3 + 38,3 + 37,7 + 33,8 + 39,9 + 38,7 + 37,0 + 31,4)) / 9
х1 = 35,767
х2 = (1*(1,1 + 1,2 + 0,4 + 0,2 + 0,1 + 0,1 + 0,1 + 0,2 + 0,33)) / 9
х2 = 0,414
у = (1*(15,7 + 16,7 + 17,5 + 18,8 + 18,0 + 18,3 + 18,5 + 19,1 + 18,0)) / 9
у= 17,844
3. Рассчитаем Var для рядов: Var = 1 / n Σ ni = 1 * ( x i – xi )2
| (x1 – x1) | -4,967 | -1,467 | 2,533 | 1,933 | -1,967 | 4,133 | 2,933 | 1,233 | -4,367 | Σ = 87,120 Σ/n = 9,680 |
| (x1– x1)2 | 24,668 | 2,151 | 6,418 | 3,738 | 3,868 | 17,084 | 8,604 | 1,521 | 19,068 | |
| (x2 – x2) | 0,686 | 0,786 | -0,014 | -0,214 | -0,314 | -0,314 | -0,314 | -0,214 | -0,084 | Σ = 1,483 Σ/n = 0,165 |
| (x2– x2)2 | 0,470 | 0,617 | 0,000196 | 0,046 | 0,099 | 0,099 | 0,099 | 0,046 | 0,007 | |
| (y – y) | -2,144 | -1,144 | -0,344 | 0,956 | 0,156 | 0,456 | 0,656 | 1,256 | 0,156 | Σ = 9,202 Σ/n = 1,022 |
| (y– y)2 | 4,599 | 1,310 | 0,119 | 0,913 | 0,024 | 0,208 | 0,430 | 1,576 | 0,024 |
4. Вычислим Cov: Cov (x,y) = 1 / n Σ ni = 1 * (xi – x)*(yi – y)
| (x1-x1)(y-y) | 10,651 | 1,679 | -0,873 | 1,847 | 1,923 | 1,549 | -0,679 | Σ = 17,673 | Σ/n = 1,964 |
| (x2 –x2)(y-y) | -1,470 | -0,899 | 0,005 | -0,205 | -0,206 | -0,269 | -0,013 | Σ = -3,250 | Σ/n = -0,361 |
| (x1-x1)(x2 –x2) | -3,405 | -1,152 | -0,037 | -0,415 | -0,922 | -0,264 | 0,369 | Σ = -6,508 | Σ/n = -0,723 |
Ответ: Var1 = 9,680 Cov1 = 1,964
Var2 = 0,165 Cov2 = -0,361
Var3 = 1,022 Cov3 = -0,723
Задача 2.
Определить коэффициенты при объясняющих переменных, для линейной регрессии, отражающих зависимость потребления картофеля от его производства и импорта, используя данные из задачи 1.
Найти: b1,2 = ?
Решение:
1. Определим Var рядов объясняющих переменных:
Var(х1) = 9,680
Var(х2) = 0,165
2. Определим Cov:
Cov(x1;у) = 1,964
Cov(х2;у) = -0,361
Cov(х1;х2) = -0,723
3. Вычислим b1 и b2 по формулам:
b1 = Cov(x1;у)* Var(х2) - Cov(х2;у)* Cov(х1;х2)/ Var(х1)* Var(х2) – (Cov(х1;х2))2
b2 = Cov(х2;у)* Var(х1) - Cov(x1;у)* Cov(х1;х2)/ Var(х1)* Var(х2) - (Cov(х1;х2))2
b1 = (1,964*0,165) – (-0,361*-0,723)/ (9,680*0,165) - (-0,723)2
b1 = 0,059
b2 = (-0,361*9,680) – (1,964*-0,723)/ (9,680*0,165) - (-0,723)2
b2 = - 1,931
Ответ: 0,059 ; - 1,931
Задача 3.
Рассчитать коэффициент А для регрессии, отражающий зависимость потребления картофеля от его производства и импорта (исп. Данные из задачи 1 и 2)
Найти: а = ?
Решение:
1. определим средние значения:
х1 = 35,767 х2 = 0,414 у = 17,844
2. Определим коэффициенты b1 и b2:
b1 = 0,059 b2 = -1,931
3. Вычислим значение коэффициента а: а = у – b1x1 – b2x2
a = 17,844 - 0,059*35,767 – (-1,931*0,414)
a = 16,533
Ответ: 16,533
Задача 4.
Рассчитать значение личного потребления картофеля, используя полученные в задаче 2 и 3 коэффициенты регрессии.
Решение:
1. Определим коэффициенты b1 и b2:
b1 = 0,059 b2 = -1,931
2. Определим коэффициент а:
а = 16,533
3. Определим вектор регрессионного значения по формуле:
[Х*]= а + b1[x1]+ b2[x2]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| [Х*] | 16,226 | 16,240 | 18,020 | 18,371 | 18,334 | 18,694 | 18,623 | 18,33 | 17,748 |
Задача 5.
Рассчитать общую, объясненную и не объясненную сумму квадратов отклонений для рассчитанной ранее регрессии по потреблению картофеля.
Найти: RSS, TSS, ESS - ?
Решение:
1. Определим средненаблюдаемое у и средне расчетное у* независимых переменных:
| Потребление у | 15,7 | 16,7 | 17,5 | 18,8 | 18 | 19,1 | 18 | Σ = 160,6 | Σ/n = 17,84 |
| у* | 16,226 | 16,240 | 18,020 | 18,371 | 18,334 | 18,330 | 17,748 | Σ= 160,6 | Σ/n = 17,84 |
у = y*
2. Определим общую сумму квадратов отклонений по формуле:
TSS = Σi = 1n ( yi - y)2
TSS = 9,202
| ( yi - y)2 | 4,60 | 1,31 | 0,12 | 0,91 | 0,21 | 0,43 | 1,58 | 0,02 | Σ= 9,202 |
3. Определим объясненную сумму квадратов отклонений по формуле:
ESS = Σi = 1n ( yi – y*)2
ESS = 7,316
| ( yi – y*)2 | 2,614 | 2,571 | 0,031 | 0,279 | 0,241 | 0,724 | 0,609 | 0,237 | 0,009 | Σ= 7,316 |
4. Определим не объясненную сумму квадратов отклонений по формуле:
RSS = Σi = 1n ( yi – y*)2
RSS = 1,882
| ( yi – y*)2 | 0,277 | 0,212 | 0,271 | 0,184 | 0,112 | 0,155 | 0,015 | 0,593 | 0,063 | Σ= 1,882 |
Ответ: 9,202 ;7,316; 1,882
Задача 6.
Вычислить коэффициент детерминации, используя данные из задачи 5
Найти: R-?
Решение:
1. Вычислим TSS и ESS:
TSS = 9,202
ESS = 7,316
2. Найдем R2 по формуле:
R2 = ESS/TSS
R2 = 7,316/9,202
R2 = 0,795
Ответ: 0,795
Задача 7.
Для оценки возможной мультиколлиниарности, рассчитать коэффиц. корреляции между рядами данных (задача 1).
Решение:
1. Найдем Var:
Var(х1) = 9,680
Var(х2) = 0,165
2. Найдем Cov:
Cov(х1;х2) = -0,723
3. Рассчитаем коэффициент корреляции:
r(x1;х2) = Cov(х1;х2)/√ Var(х1)- Var(х2)
r(x1;х2) = -0,723/3,085
r(x1;х2) = - 0,234
Ответ: - 0,234
Задача 8.
Определить несмещенную оценку дисперсии случайного члена регрессии для потребления картофеля.
Найти: Su2(u) - ?
Решение:
1. Найдем RSS:
RSS = 1,882
2. Найдем число степеней выборки
k = n-m-1
k = 9-2-1
k = 6
3. Найдем несмещенную оценку случайного члена:
Su2(u) = RSS/ n-m-1
Su2(u) = 1,882/9-2-1
Su2(u) = 0,3136
Ответ: 0,3136
Задача 9.
Рассчитать стандартные ошибки оценок коэффициента при объясняющ. переменных для модели множеств. регрессии по потреблению картофеля.
Найти: С.О.(b1), C.O.(b2) - ?
Решение:
1. Найдем дисперсию случайного члена:
Su2(u) = 0,3136
2. Найдем Var:
Var(х1) = 9,680
Var(х2) = 0,165
3. Найдем коэффиц. корреляции:
r(x1;х2) = - 0,234
4. Вычислим стандартные ошибки С.О.(b1), C.O.(b2):
С.О.(b1) = (√(Su2(u)/n * Var(х1)) * (1/1- r2 (x1;х2))
С.О.(b1) = (√(0,3136/9*9,680))* (1/1-(- 0,234))
C.O.(b2) = (√(Su2(u)/n * Var(х2)) * (1/1- r2 (x1;х2))
C.O.(b2) = (√(0,3136/9*0,165))* (1/1-(- 0,234))
С.О.(b1) = 0,0486
C.O.(b2) = 0,3724
Ответ: 0,0486; 0,3724.
Задача 10.
Рассчитать статистику Дарбина-Уотсона.
Найти: DW - ?
Решение:
1. Определим остатки в наблюдениях:
ek = yk – y*k; k = (1:n)
| y(k) | 15,7 | 16,7 | 17,5 | 18,8 | 18 | 18,3 | 18,5 | 19,1 |
| y(k)* | 16,226 | 16,240 | 18,020 | 18,371 | 18,334 | 18,694 | 18,623 | 18,330 |
| e(k) | -0,526 | 0,461 | -0,520 | 0,429 | -0,334 | -0,394 | -0,123 | 0,770 |
| ek-e(k-1) | -0,987 | 0,981 | -0,949 | 0,763 | 0,060 | -0,271 | -0,893 | 0,519 |
| ek-e(k-1)^2 | 0,973 | 0,962 | 0,901 | 0,582 | 0,004 | 0,073 | 0,798 | 0,269 |
| e(k)^2 | 0,277 | 0,212 | 0,271 | 0,184 | 0,112 | 0,155 | 0,015 | 0,593 |
(e k-e k – 1) 2= 4,562
e k2 = 1,882
2. Вычислим статистику Дарбина-Уотсона:
DW = Σ (e k-e k – 1)2/ Σ e k2
DW = 2,424
DW > 2
Ответ: т.к. DW > 2, то автокорреляция отрицательная.
Задание 3.2
Задача 1.
Рассчитать выборочное среднее для ряда данных по личным потребительским расходам на косметику (млрд. руб.):
6.3 6.6 6.8 7.0 7.1 7.4 7.9 7.8 7.4
Найти: а
Решение:
1. Запишем формулу: a=1/N*Σ Nt=1*x (t)
2. Вычислим:
а = 1*(5.9 + 6.3 + 6.6 + 6.8 + 7.0 + 7.1 + 7.4 + 7.9 + 7.8 + 7.4)/10
а = 7,02 (млрд. руб.)
Ответ: 7,02 (млрд. руб.)
Задача 2.
Рассчитать выборочную дисперсию по данным задачи 1.
Найти: σ = ?
Решение:
Похожие работы
... стал выполнять компьютер, а эконометристу осталась главным образом: постановка задачи, выбор соответствующих моделей и методов её решения, интерпретации результатов.Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. В виду большого числа факторов, влияющих на ...
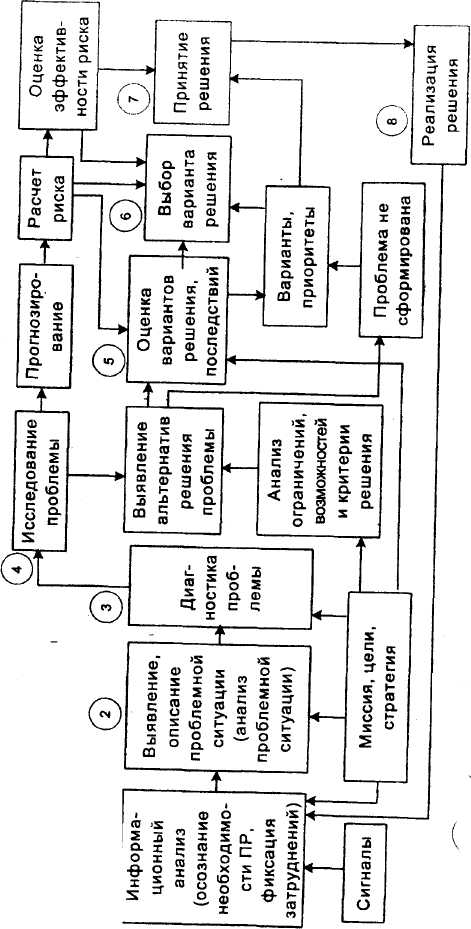
... задачи, конструктивное мышления и коммуникабельность. Коллективные формы групповой работы могут быть разными: заседание, совещание работа в комиссии и т.п. Наиболее распространены такие методы коллективной подготовки управленческих решения как "мозговой штурм", или "мозговая атака" (совместное генерирование новых идей и последующее принятие решений метод Дельфы, японская система "Кингисё". 3. ...
... эконометрические исследования и преподавание эконометрики. Экономисты, менеджеры и инженеры, прежде всего специалисты по контроллингу, должны быть вооружены современными средствами информационной поддержки, в том числе высокими статистическими технологиями и эконометрикой. Очевидно, преподавание должно идти впереди практического применения. Ведь как применять то, чего не знаешь? Приведем два ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
0 комментариев