Навигация
Применение модели оптимизации процесса управления основными средствами
3.3 Применение модели оптимизации процесса управления основными средствами
В условиях рыночной экономики необходимо неуклонное расширение объема производства, что влечет за собой наращивание производственного потенциала на новой технической основе.
Особое внимание уделяется росту и совершенствованию активной части производственных фондов.
При этом перед руководителем ООО «ЗКМ» стоит задача повышения технического уровня и качества выпускаемой продукции, значительно поднять экономичность и производительность техники, ее надежность и долговечность.
На ООО «ЗКМ» установлено различное оборудование надежность работы которого определяет эффективность и качество работы предприятия в целом.
Под надежностью понимают возможность ее длительной бесперебойной работы без остановок для ремонта и регулировок.
Замена оборудования - важная экономическая проблема. Задача состоит в определении оптимальных сроков замены старого оборудования (станков, производственных зданий и т.п.).
Старение оборудования включает его физический и моральный износ, в результате чего растут производственные затраты, затраты на ремонт и обслуживание, снижаются производительность труда, ликвидная стоимость.
Критерием оптимальности являются, как правило, либо прибыль от эксплуатации оборудования (задача максимизации), либо суммарные затраты на эксплуатацию в течение планируемого периода (задача минимизации).
При построении модели задачи принято считать, что решение о замене выносится в начале каждого промежутка эксплуатации (например, в начале года) и что в принципе оборудование можно использовать неограниченно долго. Основная характеристика оборудования - параметр состояния - его возраст t.
Таблица 10 - Исходные данные
| № п/п | Наименование | Первоначальная стоимость, тыс. р. | Срок полезного использования, лет | Затраты на содержание оборудования, тыс. р. |
| А | 1 | 2 | 3 | |
| 1 | Вычислительная техника | 829 | 5 | 131 |
При составлении динамической модели замены процесс замены рассматривается как n – шаговый, разбивая весь период эксплуатации на n шагов.
Возможное управление на каждом шаге характеризуется качественными признаками, например Хс (сохранить оборудование), Хз (заменить) и Хр (сделать ремонт).
Оборудование эксплуатируется в течение 5 лет, после этого продается.
В начале каждого года можно принять решение сохранить оборудование или заменить его новым.
Стоимость нового оборудования р0 = 829 тыс. р.
После t лет эксплуатации (![]() ) оборудование можно продать за g (t) = p02-t тыс. р. (ликвидная стоимость).
) оборудование можно продать за g (t) = p02-t тыс. р. (ликвидная стоимость).
Затраты на содержание в течение года зависят от возраста t оборудования и равны r (t) = 131 (t + 1).
Определить оптимальную стратегию эксплуатации оборудования, чтобы суммарные затраты с учетом начальной покупки и заключительной продажи были минимальны.
Способ деления управления на шаги естественный, по годам, n = 5. Параметр состояния – возраст машины – sk-1 = t, s0 = 0 – машина новая в начале первого года эксплуатации.
Управление на каждом шаге зависит от двух переменных Хс (сохранить оборудование) и Хз (заменить).
Уравнения состояний зависят от управления:
Sk = t + 1, если Хk = Хс,
1,если Хk = Хз, k = 1,2,3,4. (25)
В самом деле, если к k-му шагу sk-1 = t, то при сохранении машины (Хк = Хс) через год возраст машины увеличится на 1.
Если машина заменяется новой (Хк = Хз), то это означает, что к началу k-го шага ее возраст t = 0, а после года эксплуатации t = 1, то есть sk = 1.
Показатель эффективности k-го шага:
fk = (Хk,t) = 131 (t + 1), если Хk = Xс,
960 – 829 x 2-t, если Хk = Xз, k = 1,2,3,4. (26)
(При Хс затраты только на эксплуатацию машины возраста t, при Хз машина продается (-829 х 2-t), покупается новая (829) и эксплуатируется в течение первого года (131), общие затраты равны (-829 х 2-t + 829 + 131)).
Пусть Zk (t) – условные оптимальные затраты на эксплуатацию машины, начиная с k-го шага до конца, при условии, что к началу k-го шага машина имеет возраст t лет. Запишем для функций Zk (t) уравнения Беллмана, заменив задачу максимизации на задачу минимизации:
![]() Z5 = min 131 (t + 1) – 829 x2-(t+1), если Х5 = Хс,
Z5 = min 131 (t + 1) – 829 x2-(t+1), если Х5 = Хс,
960 - 829 x2-t - 829 x2-(t+1) , Х5 = Хз (27)
Величина 829 х 2-(t+1) – стоимость машины возраста t лет (по условию машина после 5 лет эксплуатации продается).
![]() Zk = min 131 (t + 1) + Zk+ 1(t+1), если Хk = Хс,
Zk = min 131 (t + 1) + Zk+ 1(t+1), если Хk = Хс,
960 - 829 x2-t + Zk+ 1(t+1), если Хk = Хз, k = 4,3,2,1. (28)
Из определения функций Zk(t) следует:
Zmin = Z1 (0).
Решение задачи имеет геометрический вид. На оси абсцисс откладывается номер шага k, на оси ординат - возраст t машины.
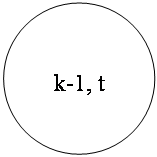
Точка (k – 1, t) на плоскости соответствует началу k-го года эксплуатации машины возраста t лет. Перемещение на графике в зависимости от принятого управления на k-м шаге показано на рисунке 1.
Состояние начала эксплуатации машины соответствует точке s*0 (0; 0), конец точкам ŝ (6; t). Любая траектория, переводящая точку s (k – 1; t) из s*0 в ŝ, состоит из отрезков – шагов, соответствующих годам эксплуатации.
Надо выбрать такую траекторию, при которой затраты на эксплуатацию машины окажутся минимальными.

 Хс
Хс![]()
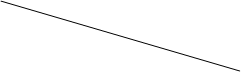 | |||
131(t+1)
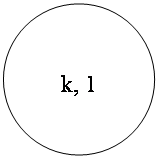 960-829x2- t
960-829x2- t
Xз
Рисунок 1 – Перемещение на графике в зависимости от принятого управления на k-м шаге
Над каждым отрезком, соединяющим точки (k – 1; t) и (k; 1 + t), запишем соответствующие управлению Хс затраты, найденные из (14): 131(t+1), а над отрезком, соединяющим точки (k–1; t) и (k; t), запишем затраты, соответствующие управлению Хз, то есть 960 – 829 x 2 –t.
Таким образом, мы разметимвсе отрезки, соединяющие точки на графике, соответствующие переходам из любого состояния sk-1 в состояние sk на рисунке 2.

Рисунок 2 - Экономико-математическая модель оптимизации процесса управления основными средствами
Например, над отрезками, соединяющими точки (k; 2) и (k + 1; 3), стоит число 393, что соответствует затратам на эксплуатацию в течение каждого года машины возраста t = 2 лет, а над отрезками, соединяющими (k; 2) и (k + 1; 1), стоит число 752 – это сумма затрат на покупку машины и эксплуатацию новой машины в течение года без «затрат» (выручки) за проданную машину возраста t лет. Следует учесть, что ![]() .
.
Проведем на размеченном графе состояний (Рисунок 2) условную оптимизацию. Начальные состояния – точки (4; t), конечные (5; t).
В состоянии (5; t) машина продается, условный оптимальный доход от продажи равен 829 x 2-t, но поскольку целевая функция связана с затратами, то в кружках точек (5; t) поставим величину дохода со знаком минус.
Состояние (4; 1). Из него можно попасть в состояние (5; 2), затратив на эксплуатацию машины 262 и выручив затем от продажи 207,25, то есть суммарные затраты равны 54, 75, и в состояние (5; 1) с затратами 545,5 – 414,5 = 131. Значит, если к последнему шагу система находилась в точке (4; 1), то следует идти в точку (5; 2) (укажем это направление выделенной стрелкой), а неизбежные минимальные затраты, соответствующие этому переходу, равны 54,75 (поместим эту величину Z*5 (1) = 54,75 в кружке точки (4; 1).
Состояние (4; 2). Из него можно попасть в точку (5; 3) с затратами 393 – 103,63 = 289,57 и в точку (5; 1) с затратами 752,75 – 414,5 =338,25. Выбираем первое управление, отмечаем его выделенной стрелкой, а Z*5 (2) = 289,57 проставляем в кружке точки (4; 2).
Рассуждая таким же образом для каждой точки предпоследнего шага, мы найдем для любого исхода IV шага оптимальное управление на V шаге, отметим его на рисунке 2 выделенной стрелкой.
Далее планируется IV шаг, анализируя каждое состояние, в котором может оказаться система в конце III шага с учетом оптимального продолжения до конца процесса, то есть, решается для всех ![]() при k = 4 уравнения. Например, если начало IV шага соответствует состоянию (3; 1), то при управлении Хс система переходит в точку (4; 2), затраты на этом шаге 262, а суммарные затраты за два последних шага равны 262 + 289,57 = 551,57. При управлении Хз затраты за два шага равны 545,5 + 54,75 = 600,25.
при k = 4 уравнения. Например, если начало IV шага соответствует состоянию (3; 1), то при управлении Хс система переходит в точку (4; 2), затраты на этом шаге 262, а суммарные затраты за два последних шага равны 262 + 289,57 = 551,57. При управлении Хз затраты за два шага равны 545,5 + 54,75 = 600,25.
Выбираем минимальные затраты 551,57, ставим их в кружок точки (3; 1), а соответствующие управления на этом шаге помечаем выделенной стрелкой, ведущей из состояния (3; 1), в состояние (4; 2). Так поступаем для каждого состояния (3; t).
Продолжая условную оптимизацию III, II и I шагов, получаем на рисунке 2 следующую ситуацию: из каждой точки (состояния) выходит стрелка, указывающая, куда следует перемещаться в данном шаге, если система оказалась в этой точке, а в кружках записаны минимальные затраты на переход из этой точки в конечное состояние.
На каждом шаге графически решалось уравнение. После проведения условной оптимизации получим в точке (0; 0) минимальные затраты на эксплуатацию машины в течение 5 лет с последующей продажей: Zmin = 2526,32.
Далее строится оптимальная траектория, перемещением из точки s0 (0; 0) по двойным стрелкам в ŝ. Получается набор точек:
![]()
который соответствует оптимальному управлению Х* (Хс, Хс, Хз, Хс, Хс). Оптимальный режим эксплуатации состоит в том, чтобы заменить машину новой в начале третьего года.
Таким образом, размеченный график (сеть) позволяет наглядно интерпретировать расчетную схему и решить задачу методом динамического программирования.
Модели и вычислительная схема динамического программирования очень гибки в смысле возможностей включения в модель различных модификаций задачи.
Можно рассматривать замену оборудования новым с учетом технического прогресса, можно учесть изменения в затратах на эксплуатацию оборудования после его ремонта, в зависимости от года эксплуатации (дороже, дешевле).
Все эти факторы можно учитывать вычислительной схемой динамического программирования.
Похожие работы
... системы трудовой мотивации и применяемых методов стимулирования труда. Целью данного дипломного исследования был анализ эффективности инвестиционного проекта строительства объекта гражданского назначения (жилого дома в Краснооктябрьском районе г. Волгограда ). Рынок жилья г. Волгограда характеризуется отставанием платежеспособного спроса от предложения, что связано с ростом стоимости ...
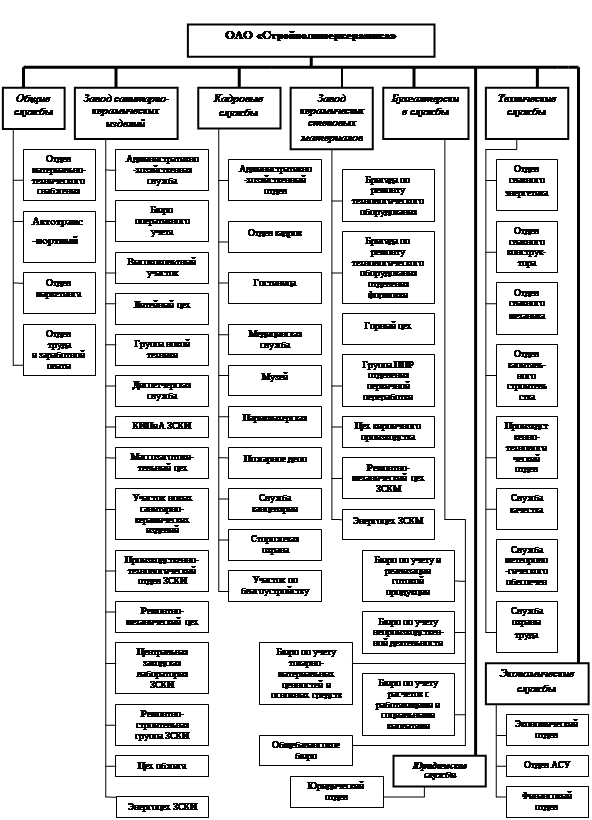
... средств и др. (интенсивные); снабженческо-сбытовая деятельность, природоохранная деятельность и др. (внепроизводственные факторы). Глава II. Анализ прибыли и рентабельности ОАО "Стройполимеркерамика" 2.1 Технико-экономическая характеристика предприятия ОАО "Стройполимеркерамика", сокращенно - СПК, (пос. Воротынск, Калужской области) является одним из ведущих предприятий России по ...
... ремонта и технического обслуживания основных средств для непрерывного совершенствования организации таких процессов [39,41]. 1.3 Правовое регулирование организации труда ремонтных служб на предприятии Правовое регулирование труда ремонтных служб предприятия связано с необходимостью регулирования всех процессов, протекающих в рамках его производственной среды. К перечню общих нормативных ...
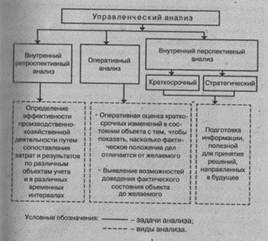
... его потенциальную способность к покрытии постоянных расходов организации. Результаты краткосрочного управленческого анализа позволяют ответить на многие вопросы, интересующие руководство организации, например: - Какая продукция (работы, услуги) наиболее рентабельна, а потому более предпочтительна для коммерческой деятельности? - Как повлияют изменения в ценовой политике организации на объемы ...
0 комментариев