Навигация
Спектральна функція детермінованих сигналів
17680
знаков
0
таблиц
15
изображений
4 Спектральна функція детермінованих сигналів
Широкого поширення набула комплексна форма представлення спектральних характеристик імпульсних сигналів, яка часто є зручнішою та компактнішою при аналізі сигналів.
Покажемо перехід до комплексної форми. Для цього використаємо комплексну форму запису ряду Фур’є (20) і запишемо співвідношення (23):
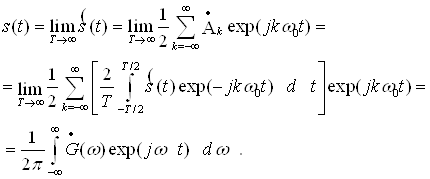(44)
У (44) враховано, що при Т
кутова частота 
перетворюється у нескінченно малий приріст 
, частота k-ї складової ряду k
– у поточну частоту 
, операція додавання переходить в операцію інтегрування. Крім того, введено позначення:
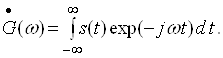(45)
Функція 
називається комплексною спектральною густиною або комплексною спектральною функцією.
Модуль комплексної спектральної густини |
| характеризує густину розподілу амплітуд спектральних складових суцільного спектру по частоті ω, а її аргумент 
|| – фазовий спектр, про що було сказано раніше.
Формули (44) та (45) описують відповідно часове та спектральне представлення імпульсного сигналу і утворюють пару перетворень Фур’є. Формула (45) дає змогу здійснити пряме перетворення Фур’є і знайти комплексну спектральну густину імпульсного сигналу s(t).
Символічно позначимо пряме перетворення Фур'є так:
(46)
Формула (44) дає можливість здійснити зворотне перетворення Фур’є і визначити імпульсний сигнал як функцію часу, якщо задана його спектральна густина 
Символічно позначимо зворотне перетворення Фур’є так:
[] = s(t). (47)
Спектральну густину можна також подати в такому вигляді:
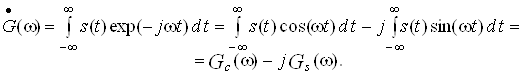(48)
Із (48) випливає, що косинус-перетворення Фур'є описує дійсну частину комплексної спектральної густини 
а синус-перетворення – її уявну частину зі знаком мінус.
Порівняння виразу для комплексної спектральної густини одиночного імпульсного сигналу (45) з виразом для комплексних амплітуд пepioдичної послідовності імпульсів (21) показує, що їх значення для частот 
відрізняються між собою лише множником 2/T. Це означає, що справедливе таке співвідношення між комплексними амплітудами k-х гармонік періодичного сигналу та значеннями комплексної спектральної густини 
– для частот, які відповідають частотам цих гармонік:
(49)
де 
– частота повторення періодичного сигналу.
Співвідношення (49) можна записати так:
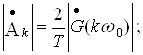(50)
(51)
Отже, модуль спектральної густини одиночного імпульсу та обгинаюча лінійчастого амплітудного спектра періодичної послідовності таких самих імпульсів збігаються за формою і відрізняються лише масштабом, аргумент спектральної густини збігається з обгинаючою лінійчастого фазового спектра даного періодичного сигналу.
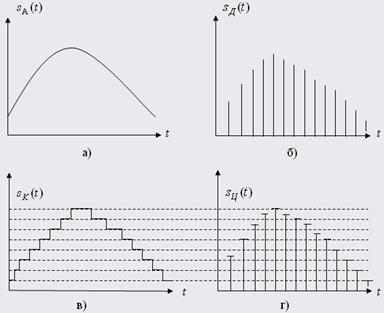
Сказане ілюструє рисунок 7, на якому зображені одиночний прямокутний імпульс, модуль його спектральної густини, періодична послідовність імпульсів та її лінійчастий амплітудний спектр.
Із збільшенням періоду T віддаль між спектральними лініями на рис.19 та коефіцієнти 
зменшуються, але так, що відношення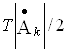 
залишається незмінним.
Комплексну функцію 
яка характеризує залежність спектра сигналу лише від його форми, називають спектральною функцією. З її допомогою на основі співвідношень (50), (51) можна визначити амплітудний та фазовий спектри сигналу незалежно від частоти його повторення.
Рисунок 7 – Спектральні характеристики одиничного прямокутного імпульсу та періодичної послідовності подібних імпульсів
Похожие работы
... Сигнал як матеріальний носій інформації є певною змінною у часі фізичної величини (напруги, струму, заряду, магнітного потоку тощо). 3 інформаційного погляду всю розмаїтість сигналів можна розділити на дві основні групи: детерміновані та випадкові. Детермінованими називають сигнали, значення яких у будь-який момент часу є точно відоме, тобто їх можна передбачити безпомилково. Такі сигнали не ...
... Генерування сигналу 5. Модулятор моделювання сигналу-носія повідомленням 3. Математичний опис сигналів при моделюванні систем зв’язку При моделюванні систем зв’язку важливим є опис реальних сигналів і завад їх математичними моделями, що базуються на основних положеннях теорії сигналів. В системах зв'язку зустрічаються різного виду детерміновані та ...
... ї зони та обмеження доступу до неї людей. На підприємстві згідно з вимогами законодавчих та інших нормативно-правових актів з питань захисту населення і територій від надзвичайних ситуацій та охорони праці повинні бути розроблені і затверджені роботодавцем: - план попередження надзвичайних ситуацій, у якому визначаються можливі аварії та інші надзвичайні ситуації техногенного та природного ...
... іших параметрів (ознаковий опис). У процесі автоматичної обробки зображення досліджуваного об'єкта формується список параметрів, часто в матричній формі або у вигляді стилізованого зображення (напівавтоматичний аналіз). Список параметрів формується в залежності від конкретних прикладних задач, тому нижче будуть наведені лише деякі приклади. Найчастіше використовувані процедури обробки: • операц ...
0 комментариев