Програма обчислення кратного інтеграла методом Монте-Карло

3. Програма обчислення кратного інтеграла методом Монте-Карло

Обчислити певний інтеграл 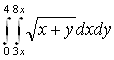. за методом “Монте-Карло” по формулі

,

де n – число випробувань ;g(x) – щільність розподілу.

3.1 Програма складена на мові програмування TURBO PASCAL 7.0

program MonteCarlo;

uses

 crt;

const k=100;

Var a,b,c,d,ng,vg,x,y,s,integral : real;

 n,i,j : integer;

 integr:array[1..k]of real;

Function f(x,y:real):real;

 Begin

 f:=Sqrt(x+y);

 end;

Function nm(x:real):real;

 Begin

 nm:=3*x;

 end;

Function vm(x:real):real;

 Begin

 vm:=8*x;

 end;

BEGIN

clrscr;

writeln('Vvedit znachennya granyts integruvannya ');

 write('a='); readln(a);

 write('b='); readln(b);

 writeln('Vvedit chyslo vyprobuvan:');

 readln(n);

 c:=nm(a);

 d:=vm(b);

 randomize;

 for j:=1 to k do

 begin

 s:=0; integral:=0;

 For i:=1 to n do

 begin

 x:=a+(b-a)*random;

 y:=c+(d-c)*random;

 ng:=nm(x);

 vg:=vm(x);

 If (y <= vg) and(y >= ng) then s:=s + f(x, y);

 end;

 integr[j]:=(b-a)*(d-c)*s/n;

 writeln(integr[j]:10:4);

 end;

 for j:=1 to k do

 Integral:=integral+ integr[j];

 writeln('Userednenyy integral=',(integral/k):10:4);

 readln;

END.

3.2Програма складена в Matematica program MonteCarlo;

{$APPTYPE CONSOLE}

uses

 SysUtils;

const k=100;

Var a,b,c,d,ng,vg,x,y,s,integral : real;

 n,i,j : integer;

 integr:array[1..k]of real;

Function f(x,y:real):real;

 Begin

 f:=Sqrt(x+y);

 end;

Function nm(x:real):real;

 Begin

 nm:=3*x;

 end;

Function vm(x:real):real;

 Begin

 vm:=8*x;

 end;

BEGIN

 writeln('Vvedit znachennya granyts integruvannya ');

 write('a='); readln(a);

 write('b='); readln(b);

 writeln('Vvedit chyslo vyprobuvan:');

 readln(n);

 c:=nm(a);

 d:=vm(b);

 for j:=1 to k do

 begin

 s:=0; integral:=0;

 randomize;

 For i:=1 to n do

 begin

 x:=a+(b-a)*random;

 y:=c+(d-c)*random;

 ng:=nm(x);

 vg:=vm(x);

 If (y <= vg) and(y >= ng) then s:=s + f(x, y);

 end;

 integr[j]:=(b-a)*(d-c)*s/n;

 writeln(integr[j]:10:4);

 end;

 for j:=1 to k do

 Integral:=integral+ integr[j];

 writeln('Userednenyy integral=',(integral/k):10:4);

 readln;

 readln;

END.

3.1Результат програми

Функція	k	N=100	N=500	N=1000	N=10000
Pascal	a=0 b=4	165.1777	162.6751	162.1815	162.1507
mathematica	a=0 b=4

Висновок

Метод Монте-Карло використовується дуже часто, часом неефективним чином. Він має деякі очевидні переваги:

а) Він не потребує ніяких свідчень про регулярність. Це може бути корисним, тому що часто дуже складна функція, властивості регулярності якої важко установити.

б) Він приводить до здійснення процедури навіть у багатомірному випадку, коли чисельне інтегрування застосувати неможливо наприклад, при числі вимірів, більшим за 10.

в) Його легко застосовувати при малих обмеженнях або без попереднього аналізу задачі.

Він володіє, однак, деякими недоліками, а саме:

а) Границі помилки не визначені точно, але включають якусь випадковість. Це, однак, більш психологічна, ніж реальна, проблема.

б) Статистична похибка зменшується повільно.

в) Необхідність мати випадкові числа.

Джерела використаної інформації

1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов втузов. – 3-е изд., перераб. И доп. – М.: Высш. школа, 1979г.

2. Ермаков С.М. Методы Монте-Карло и смежные вопросы. М.: Наука, 1971г.

3. Севастьянов Б.А. Курс теории вероятностей и математической статистики. – М.:Наука,1982г.

4. Математика. Большой энциклопедический словарь / Гл. ред. Ю.В. Прохоров. – М.: Большая Российская энциклопедия,1999г.

5. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. Изд. 5-е, перераб. и доп. М., «Высш. школа», 1977.

6. Демидович Б.П. Основы вычислительной математики. М., Государственное издательство физико-математической литературы