Навигация
1.2 Золотое сечение
В этом параграфе мы рассмотрим задачу нахождения минимума функции одной действительной переменной. Эта одномерная задача нередко возникает в практических приложениях. Кроме того, большинство методов решения многомерных задач сводится к поиску одномерного минимума.
Сейчас мы рассмотрим метод золотого сечения, применимый к недифференцируемым функциям. Будем считать, что 
задана и кусочно-непрерывна на отрезке 
, и имеет на этом отрезке (включая его концы) только один локальный минимум. Построим итерационный процесс, сходящийся к этому минимуму.
Вычислим функцию на концах отрезка, а также в двух внутренних точках 
, сравним все четыре значения функции между собой и выберем среди них наименьшее. Пусть наименьшим оказалось 
. Очевидно, минимум расположен в одном из прилегающих к нему отрезков (см. рис. 1). Поэтому отрезок 
можно отбросить и оставить отрезок 
. Первый шаг процесса сделан.
 | | | |||||||||
| |||||||||||
 | | | | | |||||||
 | |||||||||||
| | | | | |||||||
a x1 x3 x2 b
Рис. 1
На отрезке снова надо выбрать две внутренние точки, вычислить в них и на концах отрезка значения функции, и сделать следующий шаг процесса. Но на предыдущем шаге вычислений мы уже нашли на концах нового отрезка и в одной его внутренней точке 
. Поэтому достаточно выбрать внутри еще одну точку 
, определить в ней значение функции и провести необходимые сравнения. Это вчетверо уменьшает объем вычислений на одном шаге процесса.
Как выгодно размещать точки? Всякий раз мы делим оставшийся отрезок на три части (причем одна из точек деления уже определена предыдущими вычислениями) и затем отбрасываем один из крайних отрезков. Очевидно, надо, чтобы следующий отрезок был поделен подобно предыдущему. Для этого должны выполняться соотношения
.
Решение этих уравнений дает
. (4)
После проведения очередного вычисления отрезок сокращается в 
раза; после 
вычислений функции он составляет 
долю первоначальной величины (три первых вычисления в точках 
еще не сокращают отрезок). Следовательно, при 
длина оставшегося отрезка стремится к нулю как геометрическая прогрессия со знаменателем , т. е. метод золотого сечения всегда сходится, причем линейно.
Запишем алгоритм вычисления. Для единообразия записи обозначим
,
а поочередно вводимые внутренние точки будут 
На первом шаге полагаем согласно (4)
. (5)
После сравнения может быть отброшена точка с любым номером, так что на следующих шагах оставшиеся точки будут перенумерованы беспорядочно. Пусть на данном отрезке есть четыре точки 
из которых какие-то две являются концами отрезка. Выберем ту точку, в которой функция принимает наименьшее значение; пусть это оказалась 
:
. (6)
Затем отбрасываем ту точку, которая более всего удалена[3] от ; пусть этой точкой оказалась 
:
. (7)
Определим порядок расположения оставшихся трех точек на числовой оси; пусть, для определенности,
. (8)
Тогда новую внутреннюю точку введем таким соотношением[4]:
, (9)
и присвоим ей очередной номер. Минимум находится где-то внутри последнего отрезка, 
. Поэтому итерации прекращаем, когда длина этого отрезка станет меньше заданной погрешности 
:
. (10)
Метод золотого сечения является наиболее экономичным аналогом метода дихотомии применительно к задачам на минимум. Он применим даже к недифференцируемым функциям и всегда сходится; сходимость его линейна. Если на отрезке 
функция имеет несколько локальных минимумов, то процесс сойдется к одному из них (но не обязательно к наименьшему).
Этот метод нередко применяют в технических или экономических задачах оптимизации, когда минимизируемая функция недифференцируема, а каждое вычисление функции – это дорогой эксперимент.
Метод золотого сечения рассчитан на детерминированные задачи. В стохастических задачах из-за ошибок эксперимента можно неправильно определить соотношение между значениями функций в точках; тогда дальнейшие итерации пойдут по ложному пути. Поэтому если различия функций в выбранных точках стали того же порядка, что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего 
~
, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности 
~
.
Похожие работы
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
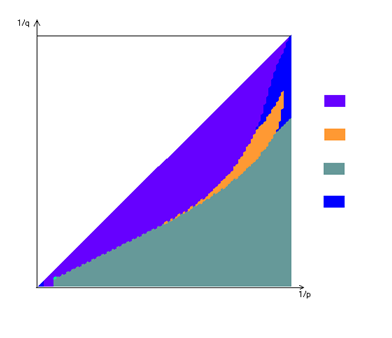
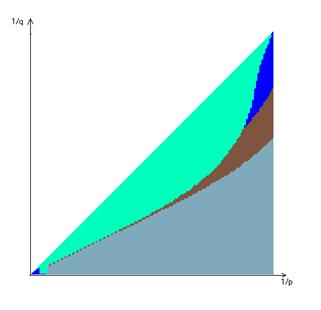
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , которые содержат неизвестную функцию, её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший ...
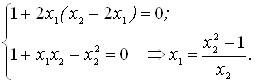
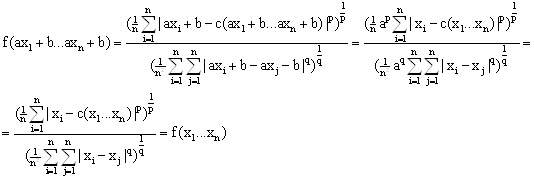
0 комментариев