Навигация
1.5 Шкали інтервалів
Якщо можна впорядкувати об'єкти настільки точно, що відомі відстані між будь-якими двома з них, то вимірювання виявиться помітно сильнішим, ніж у шкалі порядку. Природно виражати всі відстані хоча й у довільних одиницях, але однакових уздовж усієї шкали. Це означає, що рівні інтервали вимірюють однаковими за довжиною відрізками шкали, хоч де вони розміщені. Наслідок такої рівномірності шкал цього класу — незалежність відношення двох інтервалів від того, у якій шкалі їх вимірювали (тобто яка одиниця довжини інтервалу та яке значення взято як початок відліку). Справді, якщо два інтервали в одній шкалі виражаються числами Δ1х і Δ2х, а за іншого вибору нуля й одиниці — числами Δ1у і Δ2у, то, оскільки це ті самі інтервали, маємо![]() , звідки випливає, що введені шкали можуть мати довільні початки відліку й одиниці довжини, а зв'язок між показниками в них лінійний:
, звідки випливає, що введені шкали можуть мати довільні початки відліку й одиниці довжини, а зв'язок між показниками в них лінійний:
![]()
Це відношення можна виразити словами: "шкала інтервалів єдина з точністю до лінійних перетворень". Побудовані таким способом шкали називаються інтервальними.
Назва "шкала інтервалів" свідчить про те, що в цій шкалі тільки Інтервали мають зміст дійсних чисел і тільки над ними можна виконувати арифметичні операції: якщо виконати операції над самими відліками на шкалі, забувши про їх відносність, то можна одержати безглузді результати. Наприклад, якщо сказати, що температура води збільшилася вдвічі після її нагрівання від 9 до 18° за шкалою Цельсія, то для тих, хто звик користуватися шкалою Фаренгейта, це буде звучати дуже дивно, тому що в цій шкалі температура води в тому самому досліді змінилася від 37 до 42°.
Крім обчислення значення символу Кронекера та рангу спостереження єдина нова допустима операція над спостереженнями в інтер-вальній шкалі — визначення інтервалу між ними. Над інтервалами ж можна виконувати будь-які арифметичні операції, а також застосовувати всі придатні способи статистичної й іншої обробки даних.
Приклади величин, які за фізичною природою не мають абсолютного нуля чи допускають свободу вибору в установленні початку відліку й тому вимірюються в інтервальних шкалах, — температура, час, висота місцевості.
1.6 Шкали відношень
Нехай спостережувані величини задовольняють не тільки аксіомам 4 та 5, але й аксіомам адитивності:
якщо А = Р та В > 0, то А + В > Р;
А + В = В + А;
якщо А = Р та ,В = Q, то А + В = Р + Q;
(А + В) + С = А + (В + С).
Це істотно посилює шкалу: результати вимірювань у ній — "повноправні" числа; над ними можна виконувати будь-які арифметичні дії, тому що віднімання, множення та ділення — лише частинні випадки додавання. Запроваджена таким способом шкала називається шкалою відношень. Цей клас шкал має таку особливість: відношення двох значень вимірюваної величини не залежить від того, у якій шкалі зроблено вимірювання: x1/x2 =y1/y2.
Цій вимозі задовольняє співвідношення вигляду у = ах (а ≠ 0). Отже, величини, вимірювані в шкалі відношень, мають природний, абсолютний нуль, хоча залишається свобода у виборі одиниць. Приклади таких величин — довжина, маса, електричний опір, вартість.
1.7 Шкали різниць
До шкал, єдиних з точністю до лінійних перетворень, належать шкала інтервалів
(у = ах + b, а > 0, - ∞< b < +∞
і шкала відношень (у = ах, а ≠ 0). Розглянемо особливості шкал, інваріантних до зміщення
у = х + b.
Повторно застосовуючи зміщення до у (z = у + b = х + 2b), а потім до z і так далі, виявляємо, що в такій шкалі значення не змінюється після будь-якої кількості зміщень:
у = х + пb, п = 0,1,2,....
Стала величина b — це параметр шкали, який називається її періодом. Отриману шкалу називають шкалою різниць (іноді — також циклічною чи періодичною). У таких шкалах вимірюють напрямок з однієї точки (шкала компаса, роза вітрів тощо), час доби (циферблат годинника), фазу коливань (у градусах або радіанах).
Циклічні шкали — частинний випадок інтервальних. Однак угода про хоча й довільний, але єдиний для нас початок відліку шкали дає змогу розглядати показання в цій шкалі як числа, застосовувати до них арифметичні дії (доти, доки хтось не забуде про умовність нуля, наприклад у разі переходу на літній час або навпаки).
1.8 Абсолютна шкала
Розглянемо шкалу з абсолютним нулем і абсолютною одиницею. Вона не єдина з точністю до якогось перетворення, а просто єдина, унікальна. Саме такі якості має числова вісь, яку природно назвати абсолютною шкалою. Важлива особливість абсолютної шкали порівняно з усіма іншими — абстрагованість (безрозмірність) і абсолютність її одиниці. Це дає змогу виконувати над показаннями абсолютної шкали операції, неприпустимі дА показань інших шкал, — використовувати їх як показник степеня й аргумент логарифма. Числову вісь явно використовують як вимірювальну шкалу для лічби предметів, а також як допоміжний засіб — у всіх інших шкалах. Внутрішні властивості числової осі, попри ілюзорну її простоту, надзвичайно різноманітні, і теорія чисел дотепер не вичерпала їх.
Основні відомості про всі розглянуті нами вимірювальні шкали наведено в табл. 2. Можна сказати, що чим сильніша шкала, у якій виконують вимірювання, тим більше інформації про досліджуваний об'єкт, явище чи процес можна отримати. Тому природним є прагнення кожного дослідника провести вимірювання в якнайсильнішій шкалі.
Вибираючи шкалу вимірювання, слід орієнтуватися на об'єктивні відношення, яким підпорядкована спостережувана величина, і найкраще робити вимірювання в шкалі, яка максимально погоджена з цими відношеннями. Можна вимірювати й у слабшій шкалі, ніж узгоджена, але застосовувати сильнішу шкалу небезпечно: отримані дані не матимуть тієї сили, на яку орієнтовано їх обробку.
Похожие работы
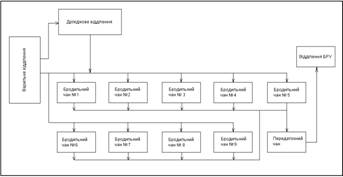
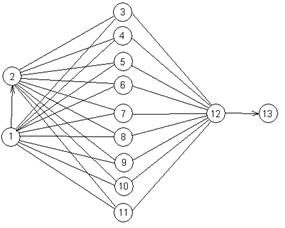
... структуру управління. При побудові автоматизованих ТК визначається кількість підсистем, розташування точок отримання інформації, розташування пунктів управління та технічна реалізація системи. 3. Використання теорії графів для структурного аналізу складних систем Теорія графів – розділ математики , який досліджує властивості різних геометричних схем (графів), які утворені множиною точок та ...
... і вирішення. Але без аналізу ми зіштовхуємося з ще більшою небезпекою втратою поліпшень тих чи інших міркувань і неправильного зважування окремих факторів. Ще одним недоліком системного аналізу є те, що він перебуває на початковій стадії свого розвитку , його методологію ще ніяк не можна назвати укоріненною, а практична застосовність і ефективність багато в чому залежать від досконалості економі ...
... язків. Все це стосується і дослідження правової системи як однієї з підсистем соціальної системи суспільства. Особливості використання системного підходу та системного аналізу у юридичних дослідженнях Використання системного підходу у юридичних дослідженнях припускає розгляд державних і правових явищ як цілісних сукупностей різноманітних елементів (складових частин), що взаємодіють між собою і ...
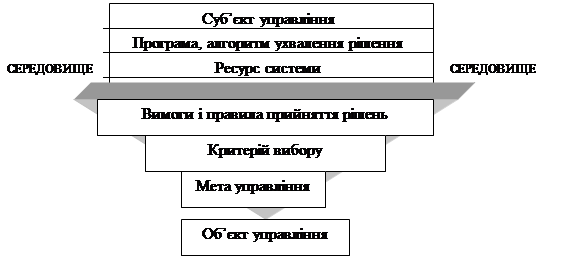
... онування. Управління досягається за рахунок відповідної організації системи, під якою розуміють її структуру та спосіб функціонування. 1. Системний аналіз управлінських проблем Системний аналіз — це певний підхід до вирішення проблем, методологія дослідження та проектування складних систем, пошуку, планування та реалізації заходів, спрямованих на вирішення проблемних ситуацій. Рис ...


0 комментариев