Навигация
Во времена Бартини 1935 года никаких компьютеров не было, а метод уже был
2. Во времена Бартини 1935 года никаких компьютеров не было, а метод уже был.
Таким образом, поскольку ТРИЗ не имеет своей математики, остается одно - обратиться к тем, у кого такая математика есть. По всей видимости, наиболее близко подошел к разгадке метода Бартини Б.А.Лабковский в книге "Наука изобретать"[9], которая вышла в 2000 году. В этой книге Б.А. Лабковский явно позиционирует себя как критик ТРИЗ. А на замену предлагает в изобретательство, в творчество, продвигать математические методы, используемые в технике, биологии, экономике, например, дифференциальные и разностные уравнения, матричную алгебру, теорию множеств, линейное программирование, теорию систем, теорию устойчивости, тензорный анализ и др.
Использование математики в творчестве, в частности, в техническом, можно только приветствовать. В этом смысле книга весьма полезная. Собственно, это нам и надо, так как мы ищем именно математический метод изобретательства Бартини.
Однако, после прочтения книги "Наука изобретать" (кстати, местами читать тяжело - уж больно затянуто, сократить бы раза в два!) складывается впечатление, что ничего хорошего в ТРИЗ нет, и она не лучше других методов технического творчества.
Особенно больно, и справедливо больно, достается некоторым законам развития технических систем - за надуманность, непоследовательность, нелогичность, перебор, а также некоторым задачам из книг Г.С.Альтшуллера - за физическую нереализуемость. Короче, в голове начинает стучать лозунг-бренд - "Даешь математику вместо ТРИЗ!". Но это как-то режет слух, уж очень революционно! На наш слух и, естественно, взгляд, гораздо приятнее будет - "Математику вместе с ТРИЗ!".
Есть, правда, исключение, когда Б.А. Лабковский похвалил ТРИЗ. Прочитаем цитату на стр.16 [9]: "Здесь авторы ТРИЗ, действительно, делают большой шаг вперед по сравнению с другими методиками, декларируя необходимость изучения внутренних свойств задачи для осуществления выбора. Альтшуллер предложил выбирать оператор R (оператор решения, добавлено мною), исходя из характера противоречия изучаемого объекта. Но в чем суть противоречия объекта? Альтшуллер отвечает на этот вопрос следующим образом: "Некоторое свойство в объекте должно одновременно сосуществовать с антисвойством". Далее автор ТРИЗ полагает, что может быть определен список, сопоставляющий то или иное противоречие соответствующему оператору, разрешающему это противоречие. Если говорить обо всем классе явлений, способных в потенциале стать изобретениями, то становится ясным, что такой список осуществить невозможно. Реальный мир неисчерпаем". И, кроме того, найденное авторами ТРИЗ множество операторов не составляет класса, так как не объединено признаками, определяющими класс. Поэтому выявленные операторы нельзя принять в качестве видов, а только лишь как набор неких частных принципов действия" (конец цитаты).
В общем-то, все правильно: и похвала и упрек. Кстати, упрек - это камешек в огород стандартов, таблицы выбора приемов разрешения ТП, т.е. нашей Contradiction Matrix, почему-то сильно любимой на Западе, и др. С похвалой согласимся, а на упрек ответим просто, по-детски: "Сам такой!".
Раз реальный мир неисчерпаем, то никуда от этого не денешься, и Лабковский не денется, когда будет составлять свою математическую модель реальной изобретательской ситуации "путем набора неких частных принципов действия". Любая модель ограничена, и еще неизвестно, сколько возможных решений будет потеряно из-за этого. Может быть, даже больше, чем не будет найдено по ТРИЗ. Собственно, Б.А.Лабковский и сам упоминает неоднократно в своей книге об этой проблеме учета "всех и вся", называя ее "проклятием размерности".
- (Интересно, - а как Р.Бартини расправлялся с этим "проклятием"? -
- Скоро уже узнаем, почитайте еще немного, еще чуть-чуть!) -
Модель изобретательской ситуации в АРИЗе очень ограничена: инструмент и изделие, отношение между ними в виде полезного действия, устраняющего нежелательный эффект, и вредного действия, противоположного полезному, а также икс-элемент (нечто неизвестное), разрешающий противоречие, и все! Для всех задач и всех изобретателей, решающих задачу по АРИЗу! Фактически Б.А.Лабковский эту структуру одобряет, поскольку одобряет физ.противоречие ("свойство-антисвойство", см. выше), которое получается из технического противоречия.
А если не одобряет, тогда он не прав, потому что вот оно, налицо! - живое и работающее, - снятие "проклятия размерности". Естественно, в этой структуре мы не учитываем, что конкретно является инструментом, а что - изделием, не говоря уж об икс-элементе; то же самое - и для характера связей: действует какая-то связь - и все, а какая - неважно (просто триада какая-то, или, просто-напросто - веполь !).
- Можно ли сработать на такой структуре? Попробуем! Тут, главное, затравку дать, запал, а дальше само пойдет - голова "доварит"!
- Впрочем, судить Вам, уважаемые читатели!-
Так как в "Науке изобретать" нет теории катастроф и гомеостатики (во всяком случае, применительно к техническому творчеству), придется обратиться к своим работам [10,11,12].
- "Сейчас нас будут формулами "душить" - скажет читатель, - придется теорию катастроф и гомеостатику изучать!"-
- "Не будем! Мы (автор этой статьи, и, надеюсь, Б.А.Лабковский тоже) хотя и ворчим иногда (см.выше) на нашего тризовского читателя, но стараемся вникать в его проблемы с математикой".-
- "Но, в ответ, Вам придется поверить на слово, что в математической теории катастроф имеется несложная формула для математической катастрофы типа "сборка",
E(x) = 0,25 x4 + 0,5 a x2 + b x, (1)
где x - координата состояния катастрофы, a и b - некоторые коэффициенты, E(x) - потенциальная функция катастрофы".
Формулу (1) можно использовать как простейшую математическую модель описания некоторого явления, процесса, системы, в которых имеется минимум потенциальной функции E(x). Если удачно назначить потенциальную функцию и выбрать из множества факторов, описывающих сложное явление (процесс или систему), всего только три - x,a,b, то получим модель, описывающую основу, "скелет", суть явления (процесса или системы). Тем самым снимается "проклятие" размерности.
В изобретательской задаче никаких проблем с удачным выбором нет. Все уже выбрано до нас. Поэтому потенциальной функцией E(x) назначим нежелательный эффект, остальная тройка - x,a,b- характеризует изделие, инструмент и икс-элемент соответственно.
Пусть x - свойство изделия, которое может быть измерено какой-нибудь подходящей физической величиной, y=a/d - свойство инструмента, которое тоже может быть измерено какой-нибудь подходящей физической величиной, z=c/e - свойство икс-элемента, которое тоже может быть измерено какой-нибудь подходящей физической величиной, d и e - коэффициенты, выравнивающие физические размерности величин x,a,b. Тогда формулу (1) можно записать в виде
E(x) = (0,25 x4 + 0,5 d y x2 + e z x)f . (2)
где f - коэффициент, выравнивающий физическую размерность величины E(x). Приведение формулы (1) к виду (2) называется масштабированием катастрофы.
Чтобы было более понятно, как использовать формулу (2), получим физико-математическую модель для известной задачи о запайке ампул с лекарством из книги "Крылья для Икара" [13].
Стеклянная ампула с налитым жидким лекарством устанавливается вертикально и капилляром вверх. Сверху подводится газовая горелка с горящим пламенем. Нежелательным эффектом является плохая запайка. Изделием является ампула с лекарством, а инструментом - пламя. Техническое противоречие формулируется следующим образом. Если язычок пламени окажется слабым, то ампула плохо запаивается, но лекарство не перегревается. Если пламя горит сильно, то капилляр ампулы оплавляется хорошо, но перегревается лекарство. Решение задачи следующее. Пламя усиливается максимально, чтобы его язычок охватывал всю ампулу. Тогда даже при возможных колебаниях пламени капилляр все-таки надежно запаивается. Для устранения перегрева лекарства ампула помещается в сосуд с водой, над поверхностью которой остается лишь капилляр. Таким образом, вода является икс-элементом и дешевым вещественно-полевым ресурсом.
Выберем за свойство изделия x высоту ампулы, начиная от кончика капилляра до основания ампулы. Тогда первое слагаемое 0,25 x4 в (2) будет иметь размерность длины в четвертой степени L4(L - длина, измеряемая в метрах, [м]). За свойство инструмента y выберем поверхность пламени, контактирующую с поверхностью изделия, т.е. ампулы. Тогда свойство y должно иметь физическую размерность поверхности или квадрата длины S=L2, а коэффициент d должен быть безразмерным. В противном случае невозможно было бы складывать первое и второе слагаемые в (2).
Можно было бы выбрать и другие свойства инструмента и изделия. Например, за свойство инструмента выбрать температуру пламени, измеряемую в градусах Кельвина, [K]. Тогда коэффициент d должен иметь физическую размерность [м2/K]. В этой задаче выбор длины L мы обоснуем тем, что качество запайки или обработки изделия оценивается именно длиной оплавленного капилляра, а для инструмента выбор поверхности S обоснуем тем, что оперативной зоной конфликта является поверхность ампулы.
- Вы можете спросить, почему именно так?
- Так в голову "пришло" (помните, голова "доварит"!). Во всяком случае, это не противоречит логике и физике задачи.
- А что из этого вышло, и для чего так надо - сейчас увидите! -
Далее выберем коэффициент e также безразмерным, тогда свойство z икс- элемента должно иметь физическую размерность куба длины или объема V=L·S·=L3. А если выберем безразмерным и коэффициент f в (2), то и нежелательный эффект или потенциальная функция E(x) будут иметь в размерности длину в четвертой степени, а именно E=L4.
Обратим внимание, что в формуле (2) знаки перед слагаемыми не учитываются, как и не учитываются численные значения коэффициентов c, d и т.д. Это связано с тем, что модель работает на уровне физических размерностей переменных x,y,z и коэффициентов, т.е. описания их физических свойств. Поэтому и в левой части, у нежелательного эффекта можно выбрать другой знак. Тогда нежелательный эффект (с точки зрения физической размерности) превращается в желательный (положительный) эффект или просто решение.
Теперь можно выстроить цепочку объектов модели с их физическими размерностями: изделие (L1) –> инструмент (L2) –> икс-элемент(L3) –> решение (L4). Наконец-то стало ясно, почему за свойство изделия выбрана высота ампулы, а за свойство инструмента - поверхность контакта и т.д., так как получена полная аналогия с широко известным в ТРИЗ трендом "точка-линия-поверхность-объем".
- " Ну, и что далее? - спросите Вы" . -
- А далее появляется на свет та самая, знаменитая "таблица [7] всех существующих и будущих физических законов", в которой представлена
Кинематическая система физических величин Р. Бартини
Собственно таблица содержит только фрагмент системы, и может быть продолжена в любую сторону путем изменения степеней m и n у Lm и Tn. В этой таблице представлены размерности физических величин в базисе длины L [м] и времени T[c]. Например, сила имеет размерность L4T-4 [м4/с4], давление - L2T-4 [м2/с4], энергия и статистическая температура – L5T-4 [м5/с4] и т.д. Числа m и n - любые целые, и для реального трехмерного пространства |m+n|3.
О возможности создания системы единиц измерений на базе только длины и времени писал Максвелл еще в 1873 году. Он же определил и размерность массы, приравняв силу инерции, равную произведению массы на ускорение, силе гравитации двух равных масс, равной квадрату массы, деленному на квадрат расстояния между тяготеющими массами (сплошной Ньютон!).
Важность LT-таблицы заключается в том, что она выражает физические законы сохранения. Например, приравнивая размерность ячейки L1T0 константе, получаем закон сохранения длины твердого тела: L=Const. Равенство L+5T-4 = Const дает закон сохранения энергии. Равенство L+2T-4=Const отражает закон Гука. Равенство L+3T-2=Const является записью закона Кеплера (отношение куба планетарного радиуса к квадрату периода вращения есть величина постоянная).
Таблицу Бартини приводит в своей книге и Б.А.Лабковский, где отмечает очень важное и полезное свойство: каждая ячейка таблицы или соответствующий закон сохранения определяет объем объектов, объединенных в класс. Действительно, многие клетки содержат не одну физическую величину, а несколько. Например, в ячейке L+3T-2 размещены две физические величины: масса и количество электричества, в ячейке L+1T0 размещены три величины: длина, емкость, самоиндукция и т.д. Более того, во многие ячейки можно дописать не указанные в таблице физические величины. Например, в системе СИ теплопроводность измеряется в [Вт/м·K]. Если вместо ватта поставить размерность мощности L+5T-5, а вместо кельвина - размерность температуры L+5T-4, то теплопроводность необходимо добавить в ячейку L-1T-1.
Текучесть расплава измеряется в [кг/с]. Подставляя вместо килограмма размерность силы L+4T-4, получаем размерность текучести расплава L+4T-5. Как видно, в исходной таблице эта величина также не приведена. Правда, если в размерности [кг/с] приведена не килограмм-сила, а килограмм-масса, тогда получим L+3T-3 (сила это или масса - должны уточнить металлурги или химики, у них тоже есть понятие текучести расплава полимеров).
Сила классификации в том, что каждый класс содержит так называемый "инвариант" - свойство, которое присуще всем элементам этого класса. П.Г. Кузнецов называет это свойство сущностью.
- В чем инвариантность или сущность длины, емкости, самоиндукции для нас, в наших изобретательских задачах?-
- В том, что все они имеют одну и ту же физическую размерность L+1T0. -
Поэтому, когда в изобретательской задаче встречаются свойства длины, емкости или самоиндукции, то с этими свойствами можно оперировать одинаковыми приемами, тем самым сокращается "проклятие размерности". Тоже самое касается и так называемых "критериев подобия", когда законы сохранения в разных отделах физики имеют одну и ту же математическую структуру. Например, если в механике в какую-нибудь формулу длина входит в квадрате, то в подобной формуле для электричества емкость тоже будет в квадратной степени.
С другой стороны, Б.А. Лабковский таблицу Бартини критикует практически за то, за что одобряет, а именно, за абстрактность, за сильную свернутость (получается, что за снижение "проклятия размерности"). Действительно, если в результате решения задачи по АРИЗу получилось, что икс-элементом является вода, то по таблице Бартини Вы этого не найдете. Нет там воды! Там только величины, которые могут быть измерены; например, расход объема [м3/с] или L+3T-1, в данном случае - абстрактная величина, поскольку этой величиной измеряется не только расход воды, но и другой жидкости, и газа, и сыпучих веществ. А в какой-нибудь другой задаче, связанной, например, с законом Архимеда, плавучестью, вода, как ответ, может быть опознана через свое, другое для этой задачи свойство, - удельный вес (физическая размерность L+1T-4) и т.д.
Но, пожалуй, главным недостатком таблицы Бартини Б.А.Лабковский считает отсутствие связи между инвариантами, т.е. отдельными клетками таблицы. Поэтому он не видит возможностей практического использования этой таблицы в изобретательстве. Во всяком случае, в главе 7 "Изобретательство и физика" [9] он уходит от хорошо свернутой таблицы Бартини и строит свою таблицу физических эффектов и сокрушается, что последняя опять выходит "на проклятие размерности".
Б.А.Лабковского можно понять. Действительно, что общего, например, между ячейкой L+2T-4 (давление) и, скажем, ячейкой L0T-1 (частота)?
Давайте разберемся, и помогут нам в этом тренды ресурсов.
Тренды ресурсов
Продолжим разбор задачи о запайке ампул. Мы остановились на том, что линия "изделие (L1) –> инструмент (L2) –> икс-элемент(L3) –> решение (L4)" для этой задачи аналогична тренду "точка-линия-поверхность-объем". Найдем этот тренд в LT-таблице. Очевидно, он находится в строке T0, где геометрическая размерность точки есть безразмерная величина L0, размерность линии - длина L1 и т.д. Каждый, кто хоть немного знает интегральное исчисление, скажет, что интеграл от дифференциала dl (точка) есть l (длина), а интеграл от ldl есть l2=S (поверхность) и т.д. (естественно, с точностью до безразмерных коэффициентов, которые мы уже договорились не учитывать).
Таким образом, по мере продвижения по тренду T0 от клетки к клетке слева направо геометрическая мерность пространства увеличивается на единицу путем умножения предыдущей мерности на L+1: Ln+1T0=LnT0 ·L+1. Можно утверждать, что размерности свойств всех элементов тренда имеют в своем составе множитель L+1, который передается по наследству от свойства к свойству, и который может быть назван геном длины. Ген длины передает всем элементам (поколениям) тренда физическое свойство: быть совокупностью (ансамблем) линий. Действительно, линия - это совокупность линий(из одной линии), поверхность - это совокупность линий, объем - это тоже совокупность линий и т.д.
Но тренд T0 в таблице неограничен как слева, так и справа, и может начинаться с любой клетки. Если он начинается с безразмерной величины L0T0, тогда все последующие поколения будут обладать свойством "быть совокупностью точек".
Выясним, как же физически или геометрически передается наследственное свойство.
Представим наше изделие, т.е. ампулу, стоящую вертикально (в деревянной кассете) и характеризуемую свойством высоты, измеряемым единицами длины. Допустим, что в начале никакого изделия и, тем более, его свойства высоты, нет. Тогда наша ампула вырождается в безразмерную точку, расположенную, например, на дне кассеты. Это будет начало отсчета. Возьмем другую точку, например, бусинку (нулевого радиуса) или пятнышко, кружок нулевой толщины (строго говоря, dl) и нулевого радиуса, и наложим его (или ee - бусинку) на первую точку, затем положим третью точку и т.д. Можно даже эти точки-кружки-бусинки накалывать на вертикальную ось как на спицу.
Наконец, накололи на спицу столько точек, что добрались до верхней точки ампулы. Получили прямую вертикальную линию нулевой толщины, но определенной длины. Именно эта линия и обладает абстрактным свойством высоты. Можно также сказать, что линия есть некоторое распределение точек вдоль высоты ампулы, и записать логическую формулу: линия = "И" точка "И" точка "И" точка...."И" точка... Формула эта выражает математическую операцию логического умножения "И"-"И" или соединения, сложения элементов в некоторую совокупность.
Вот где в первый раз проявился метод "И"-"И" Бартини - в геометрии. Недаром статья [7], где также напечатана LT-таблица, называется "Множественность геометрий и множественность физик".
Важно отметить, что свойство линии - ее высота, выражаемая в единицах длины, появляется уже при двух точках, расположенных в любых местах этой линии, например, в начале отсчета и на конце капилляра. Тогда минимальная логическая формула для линии будет такая: линия = "И" точка "И" точка.
Аналогично поступаем дальше и определяем свойство инструмента y, которое определено как поверхность пламени, контактирующая с ампулой. Так как свойство линии, измеряемое длиной, уже выяснено, то берем эту самую линию и сворачиваем ее в кольцо вполне определенного диаметра, равного диаметру ампулы и пропорционального длине с некоторым безразмерным коэффициентом. Толщину кольца выбираем, естественно, нулевой (строго, dl) - вот оно, наследственное свойство точки!
Далее такие кольца начинаем накалывать на нашу спицу, формируя из них, поверхность контакта. В районе капилляра кольца, конечно, должны быть существенно меньшего радиуса.
Ясно, что поверхность (совокупность колец) или свойство инструмента есть определенное распределение линий вдоль (ген L+1 !) высоты ампулы. Минимальная логическая формула поверхности: S = "И" линия "И" линия.
Теперь будем формировать объем или свойство y икс-элемента путем наращивания на dl того измерения, которое на предыдущей итерации было нулевым. Нулевой толщиной стенок обладает цилиндрическая поверхность, образующая из колец поверхность контакта или оперативную зону в терминологии АРИЗ. Наращиваем толщину стенок поверхности, появляется распухающий цилиндр, который и образует объем - свойство икс-элемента. В данном случае объем является определенным распределением поверхностей вдоль другого направления, перпендикулярного высоте. Иначе и объем не образовать. Но, с другой стороны, объем распределен определенным образом и по высоте ампулы: в районе лекарства - это толстый цилиндр, в районе капилляра - тонкий, да еще есть переход от толстого к тонкому. Минимальная логика объема: V = "И" поверхность "И" поверхность.
Наконец, последняя итерация - образование геометрического образа решения. Мысленно берем кубики объема (или то объемное, за что можно ухватить), и начинаем накалывать на вертикальную спицу. Получаем, что решение в пространстве, есть, по крайней мере, определенное распределение объема по высоте ампулы, т.е. по изделию. Мы-то не знаем пока, что этот объем должна занимать вода, но геометрия подсказывает, что "вода" по высоте ампулы может быть распределена по-разному. Например, снизу много - "толстый" объем, сверху мало - "тонкий" объем. Получается то же самое, когда две точки уже дают линию, а две линии -поверхность, так и два объема ("И" толстый, "И" тонкий или "И" длинный, "И" короткий (в пределе - нулевой длины)), размещенные вдоль изделия, дают минимальный геометрический образ решения.
Пространственный анализ задачи по таблице Бартини в некотором смысле аналогичен шагу 2.1 АРИЗа. Там тоже определяются ресурсы пространства, в котором находится конфликт, и куда надо вводить икс-элемент.
В чем отличие? В АРИЗе икс-элемент надо помещать в оперативную зону, т.е. в данном решении - на поверхность ампулы. Не сразу доходит до сознания, что это может быть вода: как же она удержится на поверхности? Конечно, потом дойдет (да если еще и преподаватель пояснит!), что если наливать воду, и она будет скатываться вниз по ампуле, то необходимо ампулу поставить в какой-то объем, чтобы вода не утекала. Здесь же, по Бартини, получается сразу, что икс-элемент должен иметь объем.
Еще ценной информацией является установление места размещения икс-элемента в геометрии задачи. Действительно, сначала идет изделие со своей спицей-высотой, потом, как граница разделения, инструмент со своей поверхностью, затем, по другую сторону границы, икс-элемент в своем объеме.
Мы не знаем, как Бартини называл строки своей таблицы, в частности, строку T0 . Поэтому введем свою терминологию, назовем эту строку трендом пространственных ресурсов (или пространственным трендом), да и все остальные строки тоже. Они одинаковы в том смысле, что размерность каждой последующей клетки тренда получается умножением размерности предыдущей клетки на ген длины L+1 .
Например, рассмотрим фрагмент пространственного тренда LnT-4: L-2T-4, L-3T-4, L-4T-4 или "давление - поверхностное натяжение - сила". Если L-2T-4 есть давление в точке, то L-3T-4 есть распределение давления по длине, а сила L-4T-4 есть распределение давления по поверхности.
Естественно, столбцы таблицы будем называть трендами временных ресурсов или просто временными трендами. Они одинаковы в том смысле, что размерность каждой последующей клетки тренда получается умножением размерности предыдущей клетки на ген времени T+1, если продвигаться сверху вниз, или умножением на T -1, если продвигаться снизу вверх. Аналогичны связям на пространственных трендах и интегральные или дифференциальные связи между элементами временных трендов. Например, на временном тренде L+1T m клетка с размерностью L+1T-2 является линейным ускорением, следующая клетка L+1T-1 является интегралом от линейного ускорения, т.е. линейной скоростью, следующая клетка L+1T0 является интегралом от линейной скорости, т.е. длиной и т.д.
Анализ на временном тренде ничем не отличается от анализа на тренде пространственных ресурсов, только дифференциал длины dl заменяется на дифференциал времени dt. Правда, появляются такие непривычные термины как поверхность времени L0T2 или объем времени L0T3, но мы здесь разбирать их не будем, поскольку это не повлияет на дальнейшее расследование метода Бартини. Желающие познакомиться с этим вопросом подробнее, могут обратиться к литературе [14], где в приложении есть время даже в пятой степени.
По аналогии с АРИЗом, в котором кроме оперативных пространства (зоны) и времени, анализируются также и вещественно-полевые ресурсы, определим тренды вещественно-полевых ресурсов как диагонали таблицы, проходящие слева снизу направо вверх (тренды ВПР).
Тренды ВПР (см.рис.) образуют 7 диагоналей, содержащих физические свойства с размерностями LmTn, при |m+n|3 реализуемые в трехмерном пространстве. Легко заметить, что все тренды ВПР от поколения к поколению передают ген скорости V=L1T-1. В этом - их общность. Однако есть и различие между трендами, а именно, в сумме Sn+m = n+m показателей степени n и m для размерностей LnTm.
Желтый тренд имеет сумму Sn+m =0 и передает по наследству вдоль тренда ген LnT-n. Серые тренды имеют сумму Sn+m =±1 и передают гены LnT-n±1. Голубые тренды имеют сумму Sn+m =±2 и гены LnT-n±2 . Наконец, зеленые тренды имеют сумму Sn+m =±3 и передают гены LnT-n±3.
Возникает вопрос, как же пользоваться всеми этими трендами, как найти вещественно-полевой ресурс или свойство икс-элемента?
В задаче о запайке ампул мы нашли только пространственный образ икс-элемента, т.е. одну координату - по оси L, равную L3. Значит, мы находимся в клетке L3T0 и ни вправо, и ни влево уходить с нее не можем. Иначе получим L в другой степени. Поэтому необходимо либо передвигаться по временному тренду L3Tm вверх или вниз до нужной клетки, либо остаться в исходной клетке L3T0, считая что объем есть не только пространственный ресурс, но и вещественно-полевой.
Проницательный читатель, конечно, давно догадался, что нам делать. Но мы, увы, не так проницательны, поэтому поступим по-научному. Найдем вторую координату. Ведь пока мы использовали только один фактор, одно свойство, определяющее хорошую запайку, а именно, длину оплавленного капилляра. Поэтому одну координату и получили. А второй фактор - температуру, от которой портится лекарство, пока не использовали. Давайте это и сделаем.
В работах [11,12] получено дифференциальное уравнение, описывающее эволюцию свойства икс-элемента после момента "озарения" или захвата икс-элемента системой мысленного поиска и слежения в сознании изобретателя
Kdz/dt = 3xy - az, (3)
где x и y - координаты, описывающие эволюцию конкурирующих свойств технического противоречия, z - координата, определяющая эволюцию икс-элемента в режиме слежения, K - некоторый коэффициент, зависящий от психологической инерции, а - коэффициент, зависящий от остроты мышления.
Когда инерция преодолена, свойство z икс-элемента четко фиксируется сознанием, т.е. z уже не изменяется, наступает установившийся режим dz/dt=0, и из дифференциального уравнения (3) получаем алгебраическое уравнение
z=3xy/a=Cxy. (4)
Произведение xy передает наследственную информацию о свойствах x и y "родителей", свойству z их "ребенка", т.е. икс-элементу. Для определения физического свойства z переходим от математического уравнения (4) к его физического эквиваленту в виде уравнения размерностей в базисе LT-таблицы Бартини
Lm3Tn3=C · Lm1Tn1 ·Lm2Tn3. (5)
Постоянная C является размерной константой, т.е. C=Lm4Tn4, и где все mi и nj - целые числа, положительные и отрицательные.
В уравнении (5) произведение Lm1Tn1 ·Lm2Tn3 определяет тот элемент тренда ВПР, в котором заложены свойства того и другого "родителей". Сам же тренд ВПР, проходящий через этот элемент с размерностью Lm1Tn1 ·Lm2Tn3, может быть назван родительским.
Определим родительский тренд ВПР для задачи о запайке ампул. Для этого найдем факторы, разнородно влияющие на важную потребительскую характеристику нашей запайки. Ясно, что этой характеристикой является качество запайки. Будем считать, что на качество запайки влияют всего два разнородных фактора: длина оплавленного капилляра и температура лекарства. Конечно, результат этот мы в чистом виде взяли из АРИЗа.
Теперь эти два фактора мы должны сложить, соединить, и передать нашему икс-элементу. Решение должно иметь И "хорошую" длину оплавленного капилляра, И "хорошую" температуру лекарства. Для этого используем логическое умножение "И-И": размерность длины умножаем на размерность температуры в соответствии с (5) и получаем размерность элемента на родительском тренде
L6T-4=· L+1T0 ·L5T-4
Обратите внимание, что свойства длины и температуры численно заложены в показателях степени при L и T, и при умножении размерностей эти показатели складываются. Таково второе проявление метода "И-И" Бартини.
Находим сумму Sn+m =6-4=2 . По величине Sn+m находим, что это нижний голубой тренд на рисунке. Каковы могут быть дальнейшие движения в поиске ответа? Имеются только две альтернативы: либо остаться в этой точке L6T-4 и считать это свойство искомым ресурсом икс-элемента, либо продвигаться по родительскому тренду (по диагонали) в поисках нового решения.
Почему именно по диагонали? Потому что мы ищем вещественно-полевой ресурс, а не пространственный и не временной. Для нашей же задачи о запайке мы непременно должны продвигаться по диагонали родительского тренда, так как нам необходимо пересечение с временным трендом L3Tm. По голубому тренду идем вниз налево и, наконец, находим ячейку "расход объема" с размерностью L3T-1.
Мы-то знаем, решив задачу по АРИЗу, что икс-элементом является вода, но Бартини этого пока не знает. Более того, в рассмотренной выше постановке задачи (факторы: длина+температура) для Бартини икс-элементом является некоторый поток, измеряемый в [м3/с]. И поток этот должен быть как-то распределен по высоте ампулы. Можно ли сказать, из чего состоит этот поток? Можно догадаться (в LT-таблице нет воды!), так как одним их существенных факторов является температура, а потоком в этом случае может быть поток хладоносителя или теплоносителя. Вспомним из МаТХЭМ, что термическое поле бывает или поле нагрева или поле охлаждения.
Но для других полей это не так очевидно. Даже и в этой задаче, не формулируя физического противоречия, можно прийти к решению, когда граница между нагревом и охлаждением не явно выражена. Например, можно представить, что снизу ампулу обтекает поток холодной воды, но температура воды по мере увеличения высоты ампулы растет, и в районе капилляра уже перегретый водяной пар оплавляет стекло. Конечно, здесь есть фазовый переход первого рода, изменение агрегатного состояния, но в других задачах, с другими хладоносителями и другими температурами запайки, точка фазового перехода может находиться вне диапазона, так сказать, "рабочих" температур (запайки и перегрева).
Для выхода из такой ситуации, по всей видимости, Бартини формулировал и физическое противоречие. Для задачи запайки ФП можно записать так: икс-элемент должен быть горячим, чтобы не мешать сильному пламени оплавлять капилляр, и должен быть холодным, чтобы не перегревалось лекарство. Можно ли разрешить такое ФП по методу Бартини?
Свойство "горячий" и свойство "холодный" должны передаться икс-элементу, а измеряются они оба в градусах температуры. Поэтому размерность температуры возводим в квадрат и находим элемент родительского тренда
(L5T-4) 2= L10T-8 .
Определяем сумму показателей Sn+m =10-8=2. Мы попали на тот же самый нижний голубой тренд, а, следовательно, получим то же самое решение.
Вполне возможно, что найдутся скептики, которые скажут, что все эти движения по трендам и получаемые результаты являются случайным совпадением.
Сформулируем другое ФП: длина пламени должна быть большой, чтобы хорошо запаять, и должна быть маленькой, чтобы не перегреть. По образцу и подобию предыдущего варианта возводим длину в квадрат
(L1T0) 2= L2T0 .
Определяем сумму показателей Sn+m =2+0=2. Мы снова на том же тренде ВПР!
- Что теперь скажете?.. Ах, Вы уже молчите!-
- Подождите, то ли еще будет!-
Разбирая задачу о запайке ампулы, Альтшуллер и Селюцкий указывали вариант, при котором качество запайки определялось временем нагрева ампулы: большое время - хорошая запайка, но порча лекарства, малое время - плохая запайка, но не портится лекарство. Отсюда ФП - "И" большое, "И" малое время нагрева (т.е. "хорошее" время - которое и надо!).
Возводим в квадрат (L0T1) 2= L0T2 .
Определяем сумму показателей Sn+m =0+2=2.
Вариант без подробностей и без ФП, учет только главных факторов: "И" время пайки, "И" длина капилляра:
L0T1 ·L1T0= L1T1 .
Sn+m =1+1=2.
"И" время, "И" температура:
L0T1 ·L5T-4= L5T-3 .
Sn+m =5-3=2.
После этого становится грустно: LT-таблица уже лет 40 как опубликована и валяется бесполезным хламом для тризовцев.
А ведь это - физический базис техники, возможность математического оперирования свойствами! Вот где нам наша математика боком вышла!
Да, "Бартини - это голова!" [Ю.П.Саламатов, см.выше]. А мы? Мы - пикейные жилеты! И никто нам даже палец в рот не положит! Нам остается только составить матрицу, в которой приведен баланс ресурсов для родительского тренда.
Баланс ресурсов для родительского тренда
Составим матрицу баланса ресурсов по формуле (5):
x·y·C =z. (6)
Входной фактор, х
Входной фактор, y
C=Vk=(L1T-1)k
Выход - объемный расход, z
Длина, L1T0
Длина, L1T0
V1
L3T-1
Длина, L1T0
Время, L0T1
V2
L3T-1
Время, L0T1
Время, L0T1
V3
L3T-1
Время, L0T1
Температура, L5T-4
V-2
L3T-1
Длина, L1T0
Температура, L5T-4
V-3
L3T-1
Температура, L5T-4
Температура, L5T-4
V-7
L3T-1
В этой матрице правый столбец определяет выход модели задачи, т.е. свойство икс-элемента, которое получается перемножением свойств входных факторов x и y и коэффициента С. На родительском тренде коэффициент С равен гену скорости в некоторой степени k, где k - целое число, как положительное, так и отрицательное.
Как видно, в результате анализа ресурсов получилось 6 разных значений коэффициента k, т.е. 1,2,3,-2,-3,-7. Возникает вопрос, а не могут ли быть другие значения k, например, 0 , и что же заключается в величине k?
Рассмотрим подробнее первую строку матрицы баланса ресурсов. В случае использования булевой алгебры можно записать:
большая длина пламенималая длина пламенилинейная скорость =объемный расход,
где - операция логического "И" (конъюнкция). Операнды конъюнкции образуют те внешние факторы, которые влияют на конечный результат, потребительскую функцию (качество запайки). Естественно, длина пламени может быть заменена на эквивалентную длину оплавляемого капилляра.
Первые два операнда образуют физическое противоречие, а третий операнд - линейную скорость - мы отбрасываем, решая задачу по АРИЗу. Ясно, что это приводит к трудностям поиска решения.
Но что это за линейная скорость? Вспомним задачу о запайке ампул. 25 ампул в клетках деревянной кассеты едут по конвейеру к месту запайки. В месте запайки конвейер останавливается, и 25 горящих газовых горелок смещаются вниз к капиллярам ампул. Теперь ясно, что линейная скорость - это вертикальная скорость подачи горелок, или скорость надвижения пламени на ампулу. Очевидно, этот фактор должен быть учтен наравне с физическим противоречием. Собственно, поиск этого третьего фактора у Бартини в некотором смысле аналогичен поиску фактора разрешения ФП в АРИЗе. Отличие только в том, что по Бартини известна физическая размерность этого фактора, это размерность скорости в целой степени, и для данного ФП эта степень равна единице.
Для второй строки матрицы баланса ВПР строгого ФП не получается, и формально об этом свидетельствует четная степень гена скорости, т.е. k=2. Действительно, для второй строки имеем следующее логическое уравнение:
большая длина пламенималое время запайкилинейная скоростьлинейная скорость = объемный расход.
Чисто формально этот случай сводится к предыдущему, если один операнд скорости мы логически умножим на время, тогда получим длину и строгое физ. противоречие.
Если этого не делать, то можно предположить, что вторая линейная скорость относится к скорости подачи газа в горелку или его истечения из нее (имеется в виду вертикальная составляющая скорости). Получается, что конечный результат зависит от четырех входных факторов: длины пламени, времени запайки, скорости подачи горелки и скорости протекания газа в трубе.
Баланс по третьей строке матрицы также может быть сведен к первым двум случаям, либо третья скорость будет учитывать какую-то более "тонкую" структуру, например, скорость движения на молекулярном уровне в реакции горения. Здесь уже требуются для консультации физики и химики.
Для отрицательных значений k, которые связаны с появлением температуры среди операндов логической формулы баланса ВПР, можно предполагать, что гены скорости определяют процессы оплавления стекла, движения молекул жидкого лекарства, химические реакции порчи лекарства и т.п.
В принципе, от отрицательных значений k можно уйти, поскольку при k <0 выходим на понятия длительности расстояния, поверхности времени т.п. Чтобы в это дело пока не вникать, а все-таки понять, от каких входных факторов зависит конечный результат, можно логическую формулу баланса ВПР домножить на ген скорости в какой-то положительной степени.
Например, возьмем четвертую строку матрицы баланса и домножим в ее логической формуле левую правую части на V-3. Тогда получим
Время температура линейная скорость = распределение температуры по длине,
т.е. результат (выход) будет оцениваться не по объемному расходу L3T-1 , а по другому фактору родительского тренда - L6T-4.
Осталось только показать, как получается k=0. Очень просто, и следует из формулы
расход нагретого газа V 0 =расход холодной воды.
Баланс ресурсов показывает, что Бартини работал с нескольким входными факторами, а не с двумя, как АРИЗ. Именно в этом заключается важное
Отличие метода Бартини от АРИЗ
Решение Бартини, можно сказать, более геометрично и физично. В той же задаче о запайке ампул пока еще не найденная вода, а всего лишь тепло/хладоноситель, уже получается расходуемой и распределенной по высоте, что соответствует физике и геометрии процесса, а Альтшуллер и Селюцкий сначала находят, что это вода, - на противопоставлении огню при тушении пожаров (а это, скорее, психология подпускается), а потом говорят, что воду можно (а разве она не испаряется?) сделать проточной.
Хорошее определение геометрических, временных и физических свойств икс-элемента является компенсацией за то, что не называется сам икс-элемент. По Бартини мы должны опознать его по найденным свойствам.
Если проводить аналогии между методом Бартини и ТРИЗ, то наиболее похожей на LT-таблицу Бартини является, уже упоминавшаяся выше, таблица выбора приемов устранения ТП. Генеалогию этой таблицы в серии статей подробно разобрал Л. Шуб и раскритиковал таблицу ТП еще более резко, чем Б.А.Лабковский.
Вот что пишет Л. Шуб в [15, ч.4]: "В типовых приемах недостатка больше не было (списки постоянно уточнялись). А вот вплотную подойти к выделению "типовых противоречий" до сих пор не удавалось. И главное, неясной оставалась будущая логическая связка, позволяющая безошибочно находить для каждого "типового противоречия" свой - типовой же - прием".
Бартини в своей LT-таблице нашел эту связку: на уровне физических размерностей противоречивых свойств и икс-элемента. Статья Бартини опубликована в 1965 г. Примерно в это же время, по свидетельству Л.Шуба, оформилась и таблица Альтшуллера. Эти две таблицы схожи своей, так сказать, физикой. Действительно, в обеих таблицах встречаются одинаковые физические понятия: длина, скорость, время, сила, давление, вес и т.п. Если в физике какое-либо свойство не измеряется, то его можно оценить косвенно. Например, форма может быть оценена аэродинамическим сопротивлением.
Из физики Бартини пошел в математику, в формулы размерности, и на 20-30 лет раньше, чем Альтшуллер. Альтшуллер же пошел в психологию, в стереотипы поведения, сложившиеся в глубокой древности при обращении человека с палкой, камнем, водой, огнем, простейшими орудиями труда. Древний человек не только пробы и ошибки совершал, он еще и обучался, опыта и стереотипов поведения набирался и детишкам передавал: "бьют - беги, дают - бери", опять же матрешку придумал! И это древнее, чем математика, для математики нужен достаточно высокий уровень абстрактности.
Альтшуллер был писателем-фантастом, ему были ближе психологические подходы. А Бартини все-таки был инженер-конструктор, его математика была на голову выше, чем математика Альтшуллера. Каждый работал своим методом. И если у Альтшуллера с таблицей ТП получилось, как пишет Л.Шуб, неудачное исполнение, то задумка-то была очень даже неплохой: здесь можно поработать, начиная со стереотипа конфронтации типа ФП "свой-чужой" или "плюс-минус" и переходя далее к другим стереотипам бинарных отношений. А пока у нас есть еще
Пара тестовых задач которые все знают, и которые в ТРИЗ у всех на слуху. Разберем их очень коротко, в стиле Бартини. Естественно, это перевозка шлака и молниеотводы, тривиальнее не выбрать. Между прочим, Б.А.Лабковский тоже рассматривает решения этих задач.
Вот цитата из его книги "Наука изобретать"[9, с.336]: " ...рассмотрим известное изобретение о вывозе горячего шлака. Мы помним, что высвободить ковш от горячего шлака эффективнее всего при выполнении двух условий. Во-первых, образовавшаяся корка должна быть как можно более тонкой. Во-вторых, она должна быть как можно менее прочной. Таким образом, двум следствиям соответствует одна причина. Решение (если оно возможно) проще всего отыскивается в таблице фиксированием двух следствий в одном столбце. В нашем примере следствия σв и q находятся в одном столбце со входом θ, определяющим плотность. Таким образом, мы сразу приходим к задаче увеличения пористости застывающей корки".
Здесь имеется в виду, что σв - предел прочности, а q, хотя и не определено, но можно догадаться, что это толщина корки, θ - плотность. Под таблицей понимается "Таблица физических эффектов", которую сам же автор [9] критикует за неудобство пользования из-за большой размерности.
Попробуем решить задачу по методу Бартини. Предел прочности в системе СИ измеряется в [МПа], т.е. в единицах давления. По LT-таблице находим размерность давления и умножаем на размерность толщины корки, т.е. длину, и получаем
L2T-4 · L1T0 = L3T-4 , Sn+m =3-4=-1.
Попадаем на верхний серый тренд ВПР в клетку L3T-4 . Но при движении по этому тренду никак не попасть на размерность массовой плотности L0T-2, которая находится на верхнем голубом тренде ВПР с суммой Sn+m =-2.
Что-то не получается. Давайте разберемся. А для этого посмотрим, как формулирует макро-ФП для этой задачи Г.С. Альтшуллер [16, с.147]: "Слой воздуха в ОЗ должен быть заполнен нетеплопроводным веществом, чтобы уменьшить охлаждение шлака, и не должен быть заполнен веществом, чтобы не мешать заливу и сливу шлака".
Каковы главные факторы, определяющие противоречие, и которые имеют физическую размерность? Ясно, что это теплопроводность и опять-таки толщина корки, так как отсутствие вещества в слое ОЗ означает корку нулевой толщины, а толщина опять-таки измеряется единицами длины.
Теплопроводность в системе СИ измеряется в [Вт/м·K] или, при переводе мощности и температуры в LT-базис, в L-1T-1. Находим родительский тренд
L-1T-1 · L1T0 = L0T-1 , Sn+m =0-1=-1.
Решение по Бартини с выбранными нами исходными данными из модели Альтшуллера, так и из модели Лабковского, дает один и тот же родительский тренд ВПР. Поэтому на нем и будем искать ответ, не так уж много элементов в этом тренде в нашей LT-таблице, всего-то 5 штук. Естественно, самое подходящее свойство - поверхностное натяжение с размерностью L-3T-4, определяющее капиллярно-пористую структуру, а именно, пену. И у Альтшуллера решением является пена. Если же использовать плотность L0T-2, то ее надо было бы рассматривать как входной фактор задачи (обеспечение нужной плотности корки), т.е. выше мы сделали ошибку, рассматривая плотность как выход. Второй входной фактор, естественно, - корка нужной толщины. Тогда снова выйдем на поверхностное натяжение
L0T-2 · L1T0 = L1T-2 , Sn+m =1-2=-1.
Задача о молниеотводе в формулировке [17, 9]: "Для защиты антенны радиотелескопа, спрятанного внутри пластмассового купола, нужно расставить внутри молниеотводы. Но молниеотводы - проводники, а проводники задерживают радиоволны, создают радиотень". Ответом задачи является изготовление молниеотвода из диэлектрической трубы с пониженным давлением.
Определим основные факторы, влияющие на работу молниеотвода-прототипа. Это электрическая прочность воздуха и проводимость металлического штыря, концом зарытого в землю. В системе СИ электрическая прочность измеряется в [В/м]. В вольтах измеряется разность потенциалов, которая по таблице Бартини имеет размерность L2T-2, тогда электрическая прочность будет иметь размерность L1T-2. Проводимость в базисе LT Бартини имеет размерность L-1T1 (строго говоря, такой размерности в системе СИ соответствует ом [Ом], т.е. единица электрического сопротивления, но Бартини эту клетку назвал проводимостью, поэтому будем придерживаться его терминологии). Умножаем размерность электрической прочности на проводимость
L1T-2 · L-1T1 = L0T-1 , Sn+m =0-1=-1.
Выходим на верхний серый тренд ВПР с Sn+m =-1. Размерность давления L2T-4, давление находится на верхнем голубом тренде с Sn+m =-2. Тренды не совпадают. Какой вывод? Не учтен еще какой-то основной фактор. Какой? Попробуем его найти. Для этого нужно с серого тренда перейти на голубой, т.е. уменьшить сумму Sn+m =-1 на единицу. Сделаем это следующим образом: домножим полученный результат L0T-1 на L0T-1, тогда переходим в клетку L0T-2 на голубом тренде ВПР. По размерности L0T-1 находим в LT-таблице неучтенный фактор - это частота, конечно, электромагнитного излучения радиотелескопа.
Вот почти и все. Осталось
Несколько слов о том, почему Бартини не опубликовал свой метод
Здесь могут быть следующие соображения. В 1935 году метод был, конечно, засекречен, так как Бартини докладывал его военным слушателям. Потом Бартини был репрессирован и работал в "шарашке", затем была война, потом реабилитация, так что первую свою статью [6] "Некоторые соотношения между физическими константами" Бартини с большим трудом удалось опубликовать в журнале "Доклады Академии наук СССР" только в 1965г. И то - из-за представления статьи академиком Бруно Понтекорво, тоже итальянцем. Статья была настолько оригинальна, что после ее выхода некоторые академики-физики подняли скандал: "Кто это такой Бартини, и что за мистификации печатает солидный журнал?" Жаловались в отдел науки ЦК КПСС. Бартини повезло, что о нем знали в оборонном отделе того же ЦК. Когда оба отдела состыковались, от Бартини отстали.
Допустим, что после этого шума Бартини все-таки написал бы статью, как пользоваться его таблицей. Попала бы эта статья на рецензию какому-нибудь физику.
- И что бы он сказал? -
- А вот что: -
- А где тут новое? LT-базис придумал Максвелл, а Вы заполнили клетки только известными законами, а новых не открыли - пустых-то сколько осталось!
- Вообще, Ваша таблица представляет шпаргалку для студентов, правда, хорошо организованную, сжатую (кстати, большое достоинство шпор - все знают!). А то, что по ней можно узнать, что разряд молнии зависит от свойств воздуха и сопротивления заземления, так это всем известно, откройте наши учебники физики в разделе "Электричество", там про это уже все написано-
Но все, конечно, понимают, что это только предположение. На самом деле все было не так, все было гораздо проще и идеальнее, просто ИКР!
Вот как было на самом деле.
Приходит Бартини в редакцию какого-нибудь научно-технического журнала и говорит: "Я расшифровал метод Бартини. Опубликуете? " - а ему в ответ: "Хм... бартини?? Нам бы лучше мартини!!"
Ну, как тут после этого открывать
Новые горизонты и направления развития?
Не надо забывать, что только встав на плечи гигантов, мы можем заглянуть за горизонт. И если с работами Г.С.Альтшуллера и других создателей ТРИЗ мы худо-бедно знакомы, то работы Р.О.Бартини и П.Г.Кузнецова только начинаем изучать. После П.Г.Кузнецова осталась его школа, ученики, базирующиеся, в основном, в Дубне. Они продвигают идеи Р.О.Бартини-П.Г.Кузнецова не только в физику, но и химию, биологию, экологию, экономику и другие естественно-научные и социально-экономические науки [14]. Особенно хочу обратить внимание тех тризовцев, которые используют идеи ТРИЗ в бизнесе: клетки таблицы Бартини уже расширены до свойств, которые используются при анализе организационно-экономических систем, например, мобильность L+6T-6 (это свойство в практику ввел еще П.Г.Кузнецов), экстенсия L+6T-5 , экспансия L+7T-5, маневренность L+7T-6 , интенсивность L+7T-7 и др. (А.Г.Алейников [18] - 2007 г.). Если дело пойдет такими же темпами, то скоро в LT-базисе, того и гляди, появятся понятия и свойства искусства.
Вторым важным направлением, по всей видимости, является генетика техники, передача наследственных свойств от прототипов к новым системам, или более широко, эволюция техники, ее выживаемость и приспособляемость. В этом еще больше убеждают некоторые черновые материалы, любезно присланные автору В.В.Митрофановым и Ю.Даниловским. К сожалению, в этом расследовании генетическое направление развить пока не удалось. Многое еще не ясно. Есть еще подводные камни. Желающие могут их найти и бросить в автора (см. E.mail).
Если Вы не знаете, как это делается, так можно показать.
Образец первого камня, с которым каждый может ознакомится, нам уже представил Ю.Карасик, любезно разметив на сайте "Anti TRIZ-journal" рецензию [19] на другую статью автора.
Вот второй камень: "Это сплошная ерунда! Какие там гены длины, времени? Передача наследственной информации по родительским трендам и т.п.? Разве автор статьи не знает, что во времена Бартини "генетика была продажной девкой империализма"? А Бартини хоть и был бароном, однако красным бароном, антифашистом и итальянским коммунистом, и всегда хотел, чтобы красные самолеты летали быстрее, чем черные! С этим и иммигрировал в СССР! А автор статьи несет отсебятину и еще имеет наглость приписывать ее Бартини!"
Ну, что тут ответить?
Автор, хоть и не биолог, но знает, что во времена Бартини никаких генов не было, и они были изобретены значительно позже. Однако автор хотел показать, как с этими своими генами дошел до жизни такой, когда можно легко и просто по таблице Бартини решать уже решенные альтшуллеровские задачи!
Более того, автор знает и может показать, как используя LT-таблицу размерностей физических величин, балансы ресурсов и др., Бартини решал свои задачи и получал в ответе не только эту злосчастную воду для запайки, но и всевозможные другие решения без всяких генов, шума и пыли. Практически это уже просто видно и вылезает из всех щелей статьи.
А набравшись смелости, а не наглости, как утверждает оппонент, автор имеет честь заявить уважаемым читателям, что у него есть соображения по поводу того, как Бартини решал задачу дальше, выбирая оптимальное решение из множества всевозможных.
Бартини все это делал так. Сначала он брал кассету, ампулы с лекарством, горелку, газ, пламя, и ... что там еще? Ах, да! давление и ...
... и... дальше автор устал. Он не физик, и не химик, и даже не математик! Он хочет отдохнуть, открыть окна и проветрить помещение! Пусть теперь читатели поработают бартинями (автор - и не филолог!).
В заключение поблагодарим также наших уважаемых свидетелей: В.А.Королева, А.В.Кудрявцева, Ю.П.Саламатова. Расследование базируется на их показаниях, но, если в 2197 году, когда вскроют завещание Р.Бартини, окажется, что все было не так, как на самом деле, тогда уж не обессудьте - отвечать будем вместе, у стенки и дружно:
"Evviva la Bartini!"
Список литературы
1. Королев В.А. Другая ТРИЗ. "Энциклопедия ТРИЗ", 1999.
2. Чутко И. Э. Красные самолеты. - М.: Политиздат, 1978. - 128 с.
3. Кудрявцев А.В. Роберт Бартини. "Metodolog.ru" , 2005.
4. Саламатов Ю.П. Ответ на форуме сайта "Institute of Innovative Design" от 19.10.2006.
5. Ильф И. и Петров Е. Двенадцать стульев. - М.: Художественная литература, 1974. - 295 с.
6. Ди Бартини Р.О. Некоторые соотношения между физическими константами. Доклады А к а д е м и и наук СССР 1965. Том 163, N. 4. C.861-864. http://ph-pr.narod.ru/bartini.htm
7. Ди Бартини Р.О., Кузнецов П.Г. Множественность геометрий и множественность физик. // Материалы семинара "Кибернетика электроэнергетических систем". Брянск,1974.
http://situation.ru/app/rs/lib/pobisk/ur_model_sys/ur_model_sys.htm
8. Randall Marin. TRIZ AND THE OPTIMIZATION CONJECTURE. TRIZfest-07 "Теория и практика решения изобретательских задач" Сб. докладов конференции. Москва, 2007.
9. Лабковский Б.А. Наука изобретать. - СПб.: Нордмет-Издат, 2000. - 372 c. ISBN 5-93114-013-1.
10. Бушуев А.Б. Моделирование противоречий в АРИЗ. "Metodolog.ru" , 2005
11. Бушуев А.Б. Динамический вепольный анализ в АРИЗ. "Metodolog.ru" , 2005
12. Бушуев А.Б. Х-элемент: поиск, захват, слежение. Труды Международной конференции ТРИЗФЕСТ 2006// "Три поколения ТРИЗ". Россия. СПб. 2006. с.310-317. http://www.matriz.ru/6activity/06-works/06-works-05.pdf
13. Альтшуллер Г.С., Селюцкий А.Б. Крылья для Икара: Как решать изобретательские задачи.- Петрозаводск: Карелия, 1980. - 224 с.
14. http://pobisk.narod.ru/Pr-ob-ch/003_oglav.htm
15. Шуб Л. Осторожно! Таблица технических противоречий. "Metodolog.ru" , 2006.
16. Альтшуллер Г.С. Найти идею. Введение в теорию решения изобретательских задач.- Новосибирск: Наука. Сиб. отд-ние, 1991.- 225 с. ISBN 5-02-029265-6.
17. Дерзкие формулы творчества/ Составитель Селюцкий Б.А. - Петрозаводск: Карелия, 1987. - 269 с.
18. Andrei Aleinikov. NINE NEW LAWS OF CONSERVATION: FUTURE SCIENCE HORIZONS. Allied Academies International Conference. Reno, NV, October 3-5, 2007. Academy of Strategic Management . PROCEEDINGS. V. 6, N. 2 2007, pp.5-10.
19. Karasik Y.B. TRIZ-journal as a podium for mentally ill people. Anti TRIZ-journal, December 2004, Vol.3, No.11.
Похожие работы
... обучения, yi и yj –выходные сигналы i-го и j-го нейронов. В настоящее время существует множество разнообразных обучающих правил (алгоритмов обучения). Глава IV Может ли компьютер мыслить? 4.1 Реально ли компьютерное мышление? Наконец я подошел к заключительной главе своей работы. В предыдущих главах была изложена сущность построения систем искусственного интеллекта, было рассказано о ...
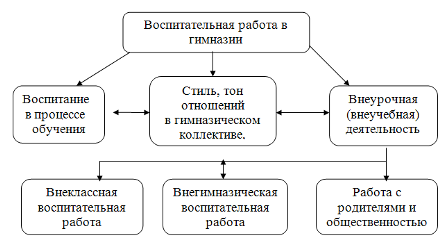
... разного типа и реализация разных направлений воспитательной работы требует конструирования разнохарактерных систем ее организации. [18, 374] Отличаясь по содержанию и направленности, воспитательная работа инновационных школ должна подчиняться модернизированной системе принципов ее организации и проводиться в формах, отвечающих требованиям разнообразия, целевой направленности, адекватности тем ...
... помогают организовывать проекты и принимать в них активное участие. Глава 2. Технология развития творческих способностей молодых специалистов социально-культурной сферы в профессиональной адаптации 2.1 Отечественный и зарубежный опыт профессиональной адаптации будущих специалистов социально-культурной сферы Профессиональная адаптация в социально-культурной сфере является одной из наиболее ...
... их активность; · культуросообразностъ, т.е. учет условий и уровня культуры данного времени и страны, родины ребенка. Его большой заслугой является разработка и решительное отстаивание идеи развивающего обучения. Именно на этой основе он построил 33 дидактических правила, согласно которым учитель должен хорошо знать своего ученика, его особенности и уровень развития, круг интересов ...

0 комментариев