Навигация
В конце вычислений по методу золотого сечения в качестве приближенного значения х* можно взять середину последнего из полученных отрезков
4. В конце вычислений по методу золотого сечения в качестве приближенного значения х* можно взять середину последнего из полученных отрезков
![]() .
.
Опишем алгоритм метода золотого сечения.
Шаг 1. Найти х1 и х2 по формулам (5). Вычислить f (x1) и f (x2).
Шаг 2. Определить ![]() . Проверка на окончание поиска: если en > e, то перейти к шагу 3, иначе - к шагу 4.
. Проверка на окончание поиска: если en > e, то перейти к шагу 3, иначе - к шагу 4.
Шаг 3. Переход к новому отрезку и новым пробным точкам. Если f (x1) £ f (x2) то положить b=x2, x2=x1, f (x2) £ f (x1), x1=b-t (b-a) и вычислить f (x1), иначе - положить a=x1, x1= x2, f (x1) = f (x2), x2=b+t (b-a) и вычислить f (x2). Перейти к шагу 2.
Шаг 4. Окончание поиска: положить
![]() ,
, ![]() .
.
Сравнение методов исключения отрезков. При сравнении прямых методов минимизации обычно учитывают количество N значений f (x), гарантирующее заданную точность определения точки х* тем или иным методом. Чем меньше N, тем эффективнее считается метод. При этом вспомогательные операции такие, как выбор пробных точек, сравнение значений f (x) и т.п., не учитываются. Во многих практических случаях определение значений целевой функции требует больших затрат (например, времени ЭВМ или средств для проведения экспериментов) и вспомогательными вычислениями можно пренебречь. А эффективность метода минимизации особенно важна именно в таких случаях, поскольку позволяет сократить указанные затраты.
Эффективность методов минимизации можно также сравнивать, на основании гарантированной точности e (N) нахождения точки х*, которую они обеспечивают в результате определения N значений f (x). Метод золотого сечения считают более точным, чем метод дихотомии, однако разница в точности в данном случае незначительна.
2.1.3 Практическое применение прямых методов одномерной безусловной оптимизации
Пусть заданы следующие параметры:

Примем ![]() и
и ![]() . Тогда
. Тогда ![]() (рисунок 7).
(рисунок 7).
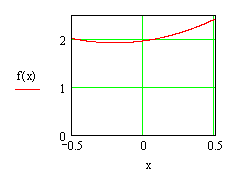
Рисунок 7 - Поведение исходной функции на заданном отрезке
Проведем несколько итерации методом дихотомии:
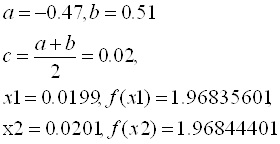
Поскольку f (x1) < f (x2), то b: =x2, a оставляем прежним. Тогда для следующей итерации:
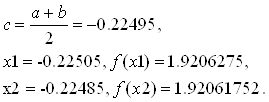
Так как f (x1) > f (x2), то a: =x1, b оставляем прежним. Тогда на третьем шаге:
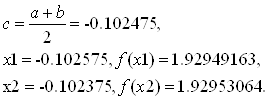
Результаты полного решения данной задачи представлены на рисунке 8. Листинг программы представлен в приложении А.
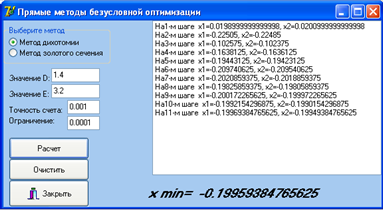
Рисунок 8 - Получение решения методом дихотомии
Для метода золотого сечения:
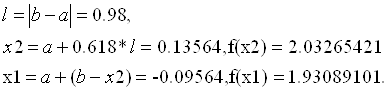
Так как f (x1) < f (x2), то b: =x2, a оставляем прежним. Тогда для следующей итерации:
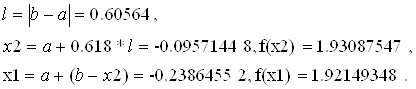
Поскольку f (x1) < f (x2), то b: =x2, a оставляем прежним. Тогда на третьем шаге:
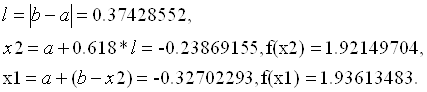
И так далее до тех пор, пока не достигнем указанной точности. Полный расчет представлен на рисунке 9. Листинг программы представлен в приложении А.
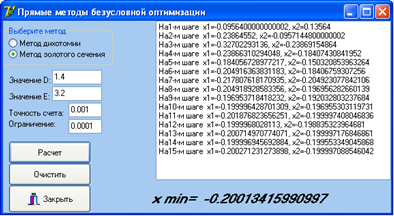
Рисунок 9 - Получение решения методом золотого сечения
2.2 Методы безусловной минимизации функций многих переменных
Теперь рассмотрим задачи оптимизации, сводящиеся к поиску точек минимума функции многих переменных на всем пространстве. В большинстве случаев такая задача бывает сложнее задачи минимизации функции одной переменной, так как с ростом размерности пространства переменных, как правило, возрастают объем вычислений и сложность алгоритмов, а также затрудняется анализ поведения целевой функции.
2.2.1 Метод циклического покоординатного спускаЭтот метод заключается в последовательной минимизации целевой функции f (x) по направлениям x1 и x2.
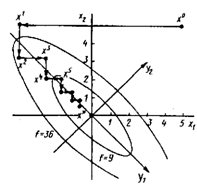
Рисунок 10 - Циклический покоординатный спуск.
Опишем этот алгоритм.
Шаг 0. Выбрать х Î En, критерий достижения точности e и шаг ![]() . Найти f (x1 (0),x2 (0)).
. Найти f (x1 (0),x2 (0)).
Шаг 1. Принять x1 (1) = x1 (0) +![]() . Определить f (x1 (1),x2 (0)). Сравнить полученное значение с значением начальной функции. Если f (x1 (1),x2 (0)) < f (x1 (0),x2 (0)), то перейти к шагу 5, если же f (x1 (1),x2 (0)) > f (x1 (0),x2 (0)), то перейти к шагу 2.
. Определить f (x1 (1),x2 (0)). Сравнить полученное значение с значением начальной функции. Если f (x1 (1),x2 (0)) < f (x1 (0),x2 (0)), то перейти к шагу 5, если же f (x1 (1),x2 (0)) > f (x1 (0),x2 (0)), то перейти к шагу 2.
Шаг 2. Принять x1 (1) = x1 (0) - ![]() . Определить f (x1 (1),x2 (0)). Сравнить полученное значение с значением начальной функции. Если f (x1 (1),x2 (0)) < f (x1 (0),x2 (0)), то перейти к шагу 5, если же f (x1 (1),x2 (0)) > f (x1 (0),x2 (0)), то перейти к шагу 3.
. Определить f (x1 (1),x2 (0)). Сравнить полученное значение с значением начальной функции. Если f (x1 (1),x2 (0)) < f (x1 (0),x2 (0)), то перейти к шагу 5, если же f (x1 (1),x2 (0)) > f (x1 (0),x2 (0)), то перейти к шагу 3.
Шаг 3. Принять x2 (1) = x2 (0) +![]() . Определить f (x1 (0),x2 (1)). Сравнить полученное значение с значением начальной функции. Если f (x1 (0),x2 (1)) < f (x1 (0),x2 (0)), то перейти к шагу 5, если же f (x1 (0),x2 (1)) > f (x1 (0),x2 (0)), то перейти к шагу 4.
. Определить f (x1 (0),x2 (1)). Сравнить полученное значение с значением начальной функции. Если f (x1 (0),x2 (1)) < f (x1 (0),x2 (0)), то перейти к шагу 5, если же f (x1 (0),x2 (1)) > f (x1 (0),x2 (0)), то перейти к шагу 4.
Шаг 4. Принять x2 (1) = x2 (0) - ![]() . Определить f (x1 (0),x2 (1)). Сравнить полученное значение с значением начальной функции. Если f (x1 (0),x2 (1)) < f (x1 (0),x2 (0)), то перейти к шагу 4, если же f (x1 (0),x2 (1)) > f (x1 (0),x2 (0)), то принять исходную точку за минимум.
. Определить f (x1 (0),x2 (1)). Сравнить полученное значение с значением начальной функции. Если f (x1 (0),x2 (1)) < f (x1 (0),x2 (0)), то перейти к шагу 4, если же f (x1 (0),x2 (1)) > f (x1 (0),x2 (0)), то принять исходную точку за минимум.
Шаг 5. Проверить условие достижения точности ![]() .
.
Если в процессе решения с шагом ![]() не получено решения, то принять
не получено решения, то принять ![]()
Этот алгоритм содержит две основные процедуры:
а) исследующий покоординатный поиск в окрестности данной точки, предназначенный для определения направления убывания f (х);
б) перемещение в направлении убывания.
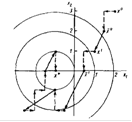
Рисунок 11 - Метод Хука-Дживса
Трактовать данный метод можно по-разному. Рассмотрим один из многочисленных вариантов.
Опишем один из алгоритмов данного метода.
Шаг 1. Выбираем начальную точку и находим в ней значение функции.
Шаг 2. Обозначим координаты начального вектора: ![]() .
.
Тогда, соответственно, угол направления движения
![]() .
.
Рассчитываем координаты 4-х точек в окрестности начальной по следующим формулам:
![]()
![]()
![]()
![]()
Находим в указанных точках значения функции. Если какое-нибудь из них оказалось меньше значения функции в точке x0, то принимаем его за исходное.
Шаг 3. Сравниваем полученные значения с f (x1 (0),x2 (0)). Если какое-нибудь из них оказалось меньше значения функции в 0-й точке точке, то принимаем его за исходное и переходим к шагу 5.
Шаг 4. Если же все полученные значения функции оказались больше исходного, то уменьшаем шаг ![]() и переходим к шагу5.
и переходим к шагу5.
Шаг 5. Проверить условие достижения точности
![]() .
.
Если данное условие не выполнено, возвращаемся к шагу 2.
2.2.3 Практическое применение прямых методов безусловной многомерной оптимизации
Пусть заданы следующие условия:
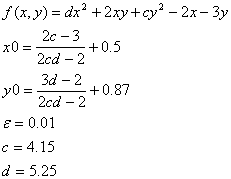
Тогда по методу циклического покоординатного спуска будет выполнен счет следующего вида:
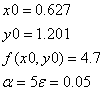
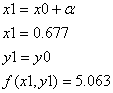
Т. к. ![]() , будем двигаться в противоположную сторону по оси абсцисс с тем же шагом:
, будем двигаться в противоположную сторону по оси абсцисс с тем же шагом:
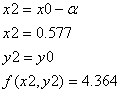
![]() ,
,
поэтому продолжаем двигаться дальше с тем же шагом в данном направлении до достижения указанной точности, в противном случае уменьшаем шаг (![]() ):
):
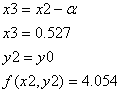
Результаты работы данного алгоритма представлены на рисунке 12. Листинг программы приведен в приложении Б.
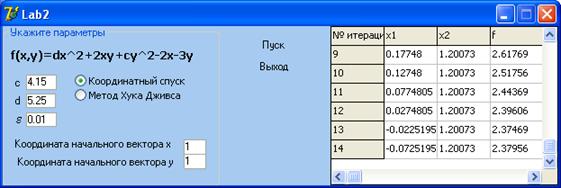
Рисунок 12 - Решение поставленной задачи методом спуска
Перейдем к методу Хука-Дживса. Обозначим координаты начального вектора: ![]() .
.
Тогда, соответственно, угол направления движения
![]() .
.
Найдем значения функции 4-х точек в окрестности начальной:
![]()
![]()
![]()
![]()
Минимальное значение функция принимает в точке2, поэтому движемся в заданном направлении 2 пока идет уменьшение функции до достижения указанной точности, в противном случае уменьшаем шаг
(![]() ):
):
![]()
Конечный результат получен на ЭВМ за 36 итераций. Результат представлен на рисунке 13. Листинг программы приведен в приложении Б.
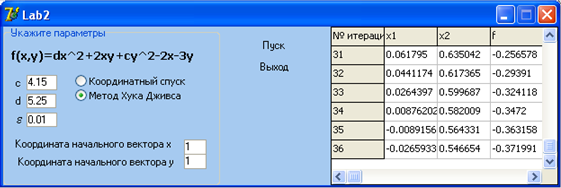
Рисунок 12 - Решение поставленной задачи методом спуска
2.2.4 Минимизация по правильному симплексуПравильным симплексом в пространстве En называется множество из n + 1 равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса.
В пространстве E2 правильным симплексом является совокупность вершин равностороннего треугольника, в E3 - правильного тетраэдра.
Если х0 - одна из вершин правильного симплекса в En то координаты остальных п вершин х1,. ., хn можно найти, например, по формулам:
 (6), где
(6), где
d1![]() , d2
, d2![]() ,
,
a- длина ребра. Вершину х0 симплекса, построенного по формулам (6), будем называть бaзовой. В алгоритме симплексного метода используется следующее важное свойство правильного симплекса. По известному симплексу можно построить новый симплекс отрaжением какой-либо вершины, например, хk симметрично относительно центра тяжести хc остальных вершин симплекса. Новая и старая вершины ![]() и хk связаны соотношением:
и хk связаны соотношением:
 , где xc
, где xc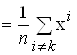 .
.
В результате получается новый правильный симплекс с тем же ребром и вершинами ![]() =2xc - хk, хi, i= 0,. ., n, i¹ k. Таким образом, происходит перемещение симплекса в пространстве Еn. На рисунке 13 представлена иллюстрация этого свойства симплекса в пространстве Е2.
=2xc - хk, хi, i= 0,. ., n, i¹ k. Таким образом, происходит перемещение симплекса в пространстве Еn. На рисунке 13 представлена иллюстрация этого свойства симплекса в пространстве Е2.
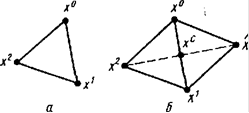
Рисунок 13 - Построение нового симплексa в E2 отрaжением точки х: a - нaчaльный симплекс х0, х1, ![]() ; б - новый симплекс х0, х1,
; б - новый симплекс х0, х1, ![]() ; центр отрaжения - точкa xc = (х0+ х1) /2
; центр отрaжения - точкa xc = (х0+ х1) /2
Поиск точки минимума функции f (x) с помощью правильных симплексов производят следующим образом. На каждой итерации сравниваются значения f (х) в вершинах симплекса. Затем проводят описанную выше процедуру отражения для той вершины, в которой f (х) принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. В противном случае выполняют еще одну попытку отражения для вершины со следующим по величине значением f (х). Если и она не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину х0 старого симплекса, в которой функция принимает минимальное значение. Поиск точки минимума f (x) заканчивают, когда либо ребро симплекса, либо разность между значении функции в вершинах симплекса становятся достаточно малыми. Опишем один из вариантов алгоритма этого метода.
Шаг 0. Выбрать параметр точности e, базовую точку х0, ребро ![]() и построить начальный симплекс по формулам:
и построить начальный симплекс по формулам:
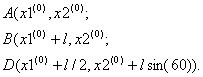
Вычислить f (х1 (0),x2 (0)).
Шаг 1. Вычислить значения f (х) в вершинах симплекса х1,. ., xn.
Шаг 2. Упорядочить вершины симплекса х0,. ., хn так, что бы f (х1 (0),x2
(0)) £ …£ £f (х1) £ f (хn-1) £ f (хn).
Шаг 3. Найти среднее значение функции:
![]() .
.
Проверить условие ![]() из учета того, что:
из учета того, что:
![]() (3.38)
(3.38)
Если оно выполнено, то вычисления прекратить, полагая х* » х0, f * » f (x0). В противном случае перейти к шагу 4.
Шаг 4. Найти
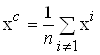
и выполнить отражение вершины хn. К примеру, для отражения вершины А следует найти точку
![]() .
.
Тогда отраженная вершина будет иметь вид:
![]() .
.
Если f (Е) <f (xn), то перейти к построению нового симплекса, иначе - перейти к шагу 5.
Шаг 5. Перейти к новому правильному симплексу с вдвое меньшим ребром (редуцирование), считая базовой вершиной х0. Остальные n вершин симплекса найти по формуле хi = (хi + х0) /2, i=1,. ., n. Перейти к шагу 1.
Геометрическая иллюстрация работы алгоритма в пространстве показана на рисунке 14, где точки х0, х1, х2 - вершины начального симплекса, а пунктиром указаны процедуры отражения.
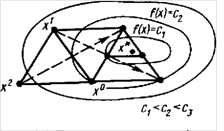
![]()
Рисунок 14 - Поиск точки минимума функции ![]() с помощью правильных симплексов в пространстве
с помощью правильных симплексов в пространстве ![]()
Замечания:
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
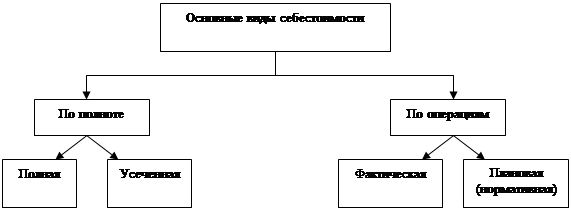
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...

0 комментариев